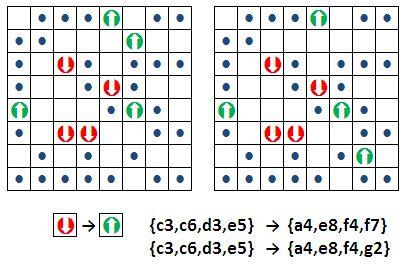
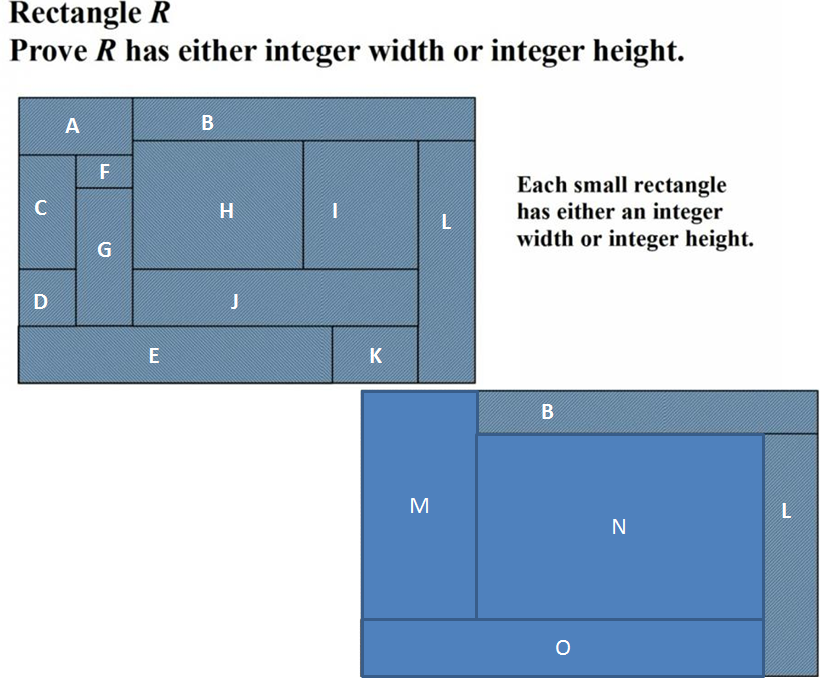
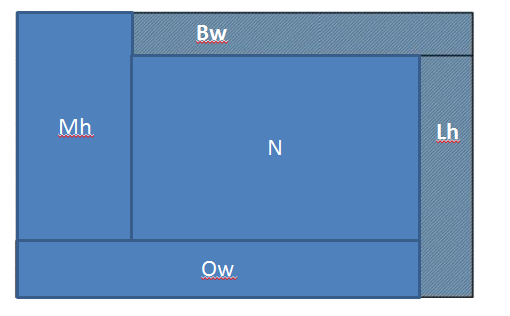
Leaderboard

Nuptual?

I assume that they also all get the clue that their numbers are unique.

With a tip of the hat to @BMAD for his interesting puzzle. For your amusement, here's an interesting spin on this genre: One night you encounter a two-hour traffic delay due to an accident (the tow truck had difficulty clearing the road.) So, for a time interval 13 of two hours you were constrained to travel at 0 mph. You called home and said, sorry dear, but I'll be two hours late getting home. The next night, for some unimaginable reason, you were also constrained to travel part of the way at 0 mph, this time for a distance of one inch. What do you say now when you call home?

In our circles you may find A laugh, a wink, a grin But pressure us we'll likely snap And send away our kin. We don't do much, we go to pot Such simple ones are we But with your hand we take command Or from you we will flee.

Agree. When I hit the send button, I realized my thinking was too simple. But instead of deleting my post (moderator privilege) I left it to take its licks.

Say we want to simulate an N sided die.

(This puzzle is from a blog called By Way Of Contradiction.) Imagine you have a circular cake, that is frosted on the top. You cut a d degree slice out of it, and then put it back, but rotated so that it is upside down. Now, d degrees of the cake have frosting on the bottom, while 360 minus d degrees have frosting on the top. Rotate the cake d degrees, take the next slice, and put it upside down. Now, assuming the d is less than 180, 2d degrees of the cake will have frosting on the bottom. If d is 60 degrees, then after you repeat this procedure, flipping a single slice and rotating 6 times, all the frosting will be on the bottom. If you repeat the procedure 12 times, all of the frosting will be back on the top of the cake. For what values of d does the cake eventually get back to having all the frosting on the top?

I swear: 1) To strangle the next person who uses 'suicide' as a verb. 2) That if I offended or hurt you in any way, I didn't mean it. 3) That I'll stop procrastinating. Tomorrow. Add whatever you swear.

Personally, the original reason I believed in God is that an adult told me he existed when I was little and, being little, I took their word. But over time, I've listened to people talk about their experiences with God and seen it with others. I think I've seen Him get me through a lot of stuff the past few years that I don't think I'd have been able to make it through alone. You could say that I got through them because I worked hard, or just because believing in a higher power has some effect psychologically, or that there were coincidences involved, but when I put it all together, those reasons just don't work for me. But if I had to give just one reason that I believe God is real, it would be that He told me so. Audibly.

eq ( 1 ) Study = not failed eq. ( 2 ) not study = failed add eq ( 1 ) & ( 2 ) study + not study = fail + not fail study ( 1 + not ) = fail ( 1 + not ) study = fail Then why should we study??

this one is pretty cute! Blonde v.s. Lawyer a lawyer sitting on a plane next to a Blonde want to pass some time and turns to her and says, "how about a trivia game, if i ask you a question and you get it right I'll pay you 10 dollars, and if you get it wrong you pay me 1 dollar. then you ask me a question, with the same conditions." blonde says, "no thanks, I'm reading a book." the lawyer says, "okay how about this, 20 dollars for getting right for you, and 20 dollars for getting wrong for me." the blonde rolls her eyes and says fine. the lawyer asks, "whats the distance from the earth to the sun?" the blonde hands him a dollar. then the blonde asks him, "what goes uphill with 3 legs and down hill with 4?" the lawyer blinks for a second and says " i have no idea, i guess you win that round." then hands her 20. "okay my turn again, i am curious, what does go up hill with three legs and down hill with 4?" the blonde hands him another dollar.

What happens in quantum statistical thermodynamics stays in quantum statistical thermodynamics...b/c no one else cares.

Out of the frying pan and on to the floor. Back into the frying pan, let hope none of the guests saw.

I would think that the only way to make ANY sense of the situation is for the woman to repeat back to the croc EXACTLY what he said to HER: "If I guess right, you'll give my baby back, if I dont, you'll eat him. That's what you'll do to him." He'd have to return the baby, because she's CORRECT NO MATTER WHAT. Eh? hehehe

I'll allow it. Nuptial Feel free to critique: Reverse a dad joke = pun = nup To marry is a clue to the whole word The last of the first = the last half of initial = -tial. Were I to rewrite, this would certainly be the place to start.

I’m the acrobat at your command, Give me a turn, or put me on the stand. I’m the sentinel, doorman you need, Give me a go, a go-ahead from me. Hit me, poke me, nail me in your wake, Without my flips, weak knees would quake. I live in one state and travel to another, Sunny side up or fumble in the other.

Two solutions. Maybe more?

It certainly should. It clearly fails a units check. Good catch.

Sorry, something got lost in copying and pasting. The site does not like the formatting used in word, so I am attaching a picture of the solution ... apologies in advance.

@MissKitten Tagging does not work on mobile and quoting is hard on mobile as well. But other than that, on a PC, one can copy-paste colors and not bother with quoting the roster altogether. Which is cool. At least from a host's PoV.

I'll go for it again:

I just saw this puzzle...it's pretty awesome...

I agree gavinksong. Sorry for not committing before. Initially I found your solution to be merely an alternative to the original. But after consideration, I think yours is better. I have switch to gavinksong's solution as it appears to be more robust. I am open to arguments for/against either TSLF or Gavin's or another better option if anyone has interest.

his answer is right. i was just asking if it extends. If i marked "answered" then no one would look at this question any more.

Given a finite set of polygons in the plane. Every two of them have a common point. Prove that there exists a straight line, that crosses all the polygons.

Just brute force. Ah, ok. Then it may be of some value for me to continue with my approach to closure, if only to check whether I get the same results.. Matches with witzar's post..

Oh wait.

I have been poking around this forum for some answers to my questions, but I cannot find them. 1. What is the system for the number of things you post before advancing in a title? (Newbie, advanced, superior, etc.) 2. How many titles are there? 3. How are VIPs granted their title? 4. Where do "stars" come in on all this? 5. Do stars go 1-5 or only 1-4 or what? Please help me make sense of this system.

An engineer, a physicist and a mathematician are staying in a hotel. The engineer wakes up and smells smoke. He goes out into the hallway and sees a fire, so he fills a trash can from his room with water and douses the fire. He goes back to bed. Later, the physicist wakes up and smells smoke. He opens his door and sees a fire in the hallway. He walks down the hall to a fire hose and after calculating the flame velocity, distance, water pressure, trajectory, etc. extinguishes the fire with the minimum amount of water and energy needed. Later, the mathematician wakes up and smells smoke. He goes to the hall, sees the fire and then the fire hose. He thinks for a moment and then exclaims, "Ah, a solution exists!" and then goes back to bed.

Getting my sister in trouble for trolling me in college; it was totally worth it!!!

out of the frying pan and-------onto the automatic waterfall glazing machine!

Pandas would never run in the first place.

Thanks for the suggestion. If anybody could draw some quality vector graphics symbolizing BrainDen (eg. including taser) then I will consider putting it on 404 page

Agreed. One up this if you are a veteran of the great Brainden Blackout!

Yeah that was the rain. The ark was in the water for about 150 days though.

noah took onto the ark: Genesis 7: 2, where God tells Noah: 'Of every clean beast thou shalt take to thee by sevens, the male and his female: and of the beasts that are not clean by two, the male and his female' so he either took 7 males and 7 females of the clean ones, or just seven in total, depending on how you understand the sentence. the idea of two by two is only relevant to unclean animals (like pigs, camels, eels, snails etc etc). gotta love QI

great example of why math can't be done under the wrong assumptions.