plasmid

Slightly better

Thanks for catching that DejMar. I'll think about how it could be made even better.

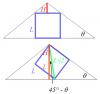
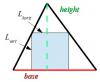
I got the same answer as gavinksong, with a little different approach. Edit: I guess I ought to attach that figure I was talking about ^.^

This somewhat reminds me of the story of the surprise execution. A prisoner was sentenced to death with the execution to take place within one week. But the judge also stipulated that the prisoner's execution should come unexpectedly, as it would be cruel to have him know that death would be imminent within 24 hours. The prisoner knew all of this. The prisoner reasoned that he could not be executed seven days after the sentence, because if he were not executed on the sixth day then he would know that he would be executed on the seventh, and that would violate the judge's ruling. For all practical purposes, the prisoner would have to be executed within six days. But that means that he couldn't be executed on the sixth day – if he made it past the fifth day and he knew he couldn't be executed on the seventh day, then he would know that he was to be executed on the sixth day, which would violate the judge's ruling. Continuing on with that sort of logic, the prisoner concluded that he could not be executed at all! The prisoner was then executed two days after the sentence, which came as a complete surprise to him in accord with the judge's ruling. The moral of the story is:

How about slightly modifying bonanova's criteria. "If the statement were posed to the UTM, the UTM would answer False. If any rational third answerer (who you can call observer X if you like, and may be human, machine, or flying spaghetti monster) were told that the statement was being posed to the UTM, then observer X would say that the statement is True."

I think you could only assert that those statements are true if you first prove that there cannot be a universal truth machine.

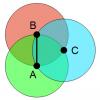
I agree with k-man. Suppose there are more than two sides with length AB and, as shown in the previous paragraph, they each must include at least one of points A and B. In that case, two of the three sides must both fall on the same side of line AB. The only way you could have two sides of the polygon of length AB that fall on the same side of AB and are within the intersection of the circles at A and B is if you pick the point C at the intersection of the circles centered on A and B to form sides AC and CB. If you have a third side that is a distance AB away from point B (or point A) on the opposite side of AB as point C, then it must have a vertex somewhere on the perimeter of circle B (or A). But if it has a vertex on the perimeter of B and is on the opposite side of line AB as point C, then that vertex's distance from point C will be larger than AB and you would violate the initial statement that AB is a longest diagonal. Edit: added side note

You should be able to make a cut face be any proportional size compared to an initial face, but whether (and how) you could make all of the cut faces be larger than the remainder of the initial faces is not clear. For what it's worth: if you cut off the vertices such that each plane of cutting is halfway between a vertex and its opposite face, that would create an octohedron where the remainder of the original faces are indistinguishable from the newly cut faces. If you take an octohedron and start shaving away one of its faces, I think that face might get larger before it gets smaller again, but I haven't done the math.

This assumes that the area left over from each of the initial faces is greater than the area of any face formed by a cut vertex,

Happy 2015, PG, and that's a nice way to start off the year!

Not what I have in mind, but a good answer to be sure and I'll think about counting it as an acceptable alternate. I'm thinking of something that might be a slightly better fit for the last stanza.

At sides of my cap A duo of flaps They certainly won't stop the winds And firmly in place Are goggles on face The mask to my curvature bends The skis on my feet Are nice and are neat But sliding's a skill that they lack I've poles in my hand So balance I can With arm tethered fast behind back Edit: changed def'nitely to certainly, to improve poetic meter

Suppose you have a bacterial strain growing in a flask where nutrients are not limiting. The bacteria will grow and divide after replicating their genomes, but cell division isn't perfect so their progeny will be viable and reproductive 99% of the time. You engineer a substrain of the bacteria by adding a gene to its genome that improves its probability of replicating to form viable offspring, but that adds to the size of the bacterial genome so it takes longer to replicate. Will the engineered bacteria outgrow the original strain? How much of an improvement in offspring viability would be needed to do so? Some numbers that might be needed (or might be red herrings): Let's say you're working with E. coli with a genome size of about 5,000,000 base pairs, and the gene you're introducing is on the small side at 1,000 base pairs. The typical doubling time for E. coli in optimal laboratory culture conditions is about 20 minutes, and let's assume that the doubling time is proportional to the genome size. You're growing them in a flask with 50 ml of media and starting with an inoculum of 1,000 cells of each bacterial strain in the flask, and assume growth will be exponential until they reach a concentration of 5 x 108 cells/ml. Would the answer change if, instead of working with a bacteria, you're working with a virus? Say the virus infects a host cell and utilizes all of the nutrients in the cell to make new virions before killing it and releasing its progeny, and the number of progeny made is inversely proportional to the viral genome size but the time until the cell dies is not affected. If you're working with an adenovirus, its genome size is 36,000 base pairs and let's say it can normally produce 500 virions from one of the host cells you're working with after three days. You start with a petri dish with 107 host cells and infect it with 100 infectious viral particles. Suppose the gene doesn't improve the efficiency of viral replication, but instead reduces its propensity to infect a cell as it floats by? The starting viral strain has a 10% probability of infecting each cell it passes over (note to any biologists out there: that number is completely made up), cells are distributed uniformly on the dish (call it a hexagonal tiling if that will make the math easier), and a virion will travel in a straight line until it infects a cell since it doesn't have to contend with an immune system. Assume that a cell that's infected with one virion will make just as many progeny as a cell that's infected with multiple virions, and the time spent floating is negligible compared to the duration of infection.

Certainly an interesting take on it... I had to look that up to see what you were talking about, which of course means it wasn't what I had in mind. I think I ought to go ahead and say what this one's about.

Nevermind, misread

I think I'm mis-translating from Math to English. In my mind, this says: Find a and b such that there is no real x for which a < q < b if and only if q = x3 + 1/x3, for all values of q But the thing on the left of the "if and only if" is true for an open range of values of q while the thing on the right of the "if and only if" is true for exactly one value of q (except when x=0). So the "if and only if" can never be satisfied. Do you have a different interpretation of the OP in mind?