plasmid

I think I see what you (gavinksong) are getting at now, and also why you couldn't give a counterexample... that seems like it would actually be very hard to do. But it would probably be necessary in order to show that any of the values of d that I excluded as unable to reach all-up again could actually reach that state, or at least come up with a proof that such a solution must exist even if you can't explicitly solve for it. It might take me a while to come up with a decent argument for the existence or nonexistence of such a solution.

Edit: misunderstood the point you were making in the previous post, will think about it some more. It's saying that the part showing which numbers can lead to an all-up position again is ok, but the part saying that there are no other solutions is not convincingly rigorous, correct?

That statement of my current answer is correct, and could be amended with "and no other solutions exist". Try as I might, I can't see a loophole where the argument would break down. One point that might be worth clarifying in case it's causing problems: Can you give a counterexample, or would it be too much of a blatant hint if you did?

It doesn't seem that difficult to see, at least for the solution I came up with.

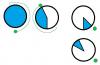
What happens when you make it around the circle if d is not divisible by 360? For example, if d is 200 degrees, then after the first cut&flip the cake from 0-200 degrees will be frosting down and the cake from 200-360 degrees will be frosting up. You'll then make a slice covering the last 160 degrees that wasn't covered already, plus another 40 degrees. Does every point on the cake within the area that gets flipped go from being frosting up to frosting down, as if it were inverted on its vertical axis or as if all slices including previously made cuts are rotated independently? Or does the entire 200 degree slice get rotated en-bloc around an axis going from the middle of its arc to the center of the circle (regardless of whether there are already previously made cuts within that slice)? In the figure, if the cake has blue frosting and the cutter is green, the first of those scenarios would produce the outcome on the top and the second scenario would produce the outcome on the bottom when he's about to make the third slice.

It omits the corners. The "while" statement is part of a "do ... while" loop surrounding the code that selects random numbers for x and y, so it keeps "do"-ing the loop "while" x2 + y2 > 1 and it stops generating new random numbers once it reaches a value that's not >1. Just a suggestion: since we do not really know if rand(..) is going to yield well-distributed points, it may make more sense to just just step x and y linearly over small increments. Ok, I could do that after I get home from work. Edit: OK, I did that and still got the same answer: 72.5% for a square and 72% for a circle.

I'm not sure why the post gets messed up when I try to quote Bonanova's argument, but I can't quote it without wrecking its formatting.

Sure enough, when I modified the Java code to also calculate the probability of a triangle drawn from a unit circle to be obtuse, it wasn't ~72.5% like a unit square. It was ~72%. Gyah.

That's a good point that arises when the available area becomes finite, and it seems very difficult to quantify that effect. And now Perl is agreeing with Java that the answer is about 72.5% if you pick points from a unit square. The code is so short that there doesn't seem to be much of a place for bugs to hide, and like the Java code it just depends on dot products which seem fairly straightforward. Edit: It might be that the shape from which the points were selected impacts the probability that they form an obtuse triangle. And if that's the case, it's probably impossible to say what to expect if the three points are chosen from an infinite plane without boundaries -- were they drawn from an an infinitely large square with probability 72.5% or an infinitely large circle with probability 75%?

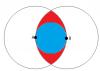
I'm not sure I follow. If you pick any three points randomly (keeping it in a finite area to make things comprehensible) and call them X, Y, and Z, then one of the three sides XY, YZ, or ZX must be the longest, and you can relabel the points so that the longest side has points A and B and make the leftover point be C. The points were all uniformly chosen in whatever area was available; the limitation of where point C could lie purely stems from having labeled A and B as the termini of the longest edge. Put another way: point C could fall outside the red and blue areas, but if it did then you would just relabel the points so it's no longer labeled C. I really do think the answer is probably 75% instead of 64%, but I'm not completely sure what the hole in the 64% argument is. I get the feeling that there's something subtle going on that makes the probability distribution of point C within the red and blue regions become non-uniform and denser in the blue region, but I can't tell exactly what it is. Edit: Plus, Java is telling me that it's about 72.5% It's seldom that I favor theory over experiment, but in this case I still think 75% is more likely correct.

The point I'm trying to make is that, unless there's a clear reason why one of the 100% or 75% or 64% answers should be "correct" while the others have some sort of flaw, then the types of arguments on which all of these answers are based should be viewed with suspicion. This seems to have a similar logical trap as the famous problem: "There are two envelopes filled with money and you are allowed to take one of them for yourself. They appear identical, but you know that one of them has twice as much money as the other. You take one of the envelopes and open it to find out how much is inside, and then you are given the opportunity to switch and take the other envelope instead. Should you switch?"

The first point in blue is fine -- you can simply say that there's a 1/2 chance that both breaks will fall on the same half of the stick if you prefer. There's a 50% chance that both breaks will NOT fall on the same half of the stick (so neither the leftmost nor rightmost fragments are greater than half the original length). Out of that 50% where the breaks are on different sides, 50% of those scenarios will have the middle piece be larger than half of the entire stick. So 25% of the time all three pieces will be less than half the size of the original stick.

To start things off, it's conjuring thoughts of Are we to use spoilers here?

Can you counter my arguments that the answer is 75% or 64%?

Suppose you were to ask someone to pick two points, defining A and B as the first and second points that they pick, and then pick a third point C. This is essentially what's being done in the arguments that the the probability of being obtuse is one. After they've picked points A and B but before they've picked point C, you can define the distance A-B based on the coordinates of those points. You can then a circle of radius A-B around point A. When you place point C somewhere in the infinite plane, there will be a finite amount of space within that circle and an infinite amount of space outside that circle where C could fall. So the probability that C will lie inside that circle (and therefore the distance A-C will be less than A-B) is zero while the probability that C will lie outside that circle (and therefore the distance A-C will be greater than A-B) is one. That appears to violate the OP's statement that the points are chosen randomly -- intuition says that if you pick three points randomly, then there should be a 50/50 chance that the second randomly chosen point is closer to the first point than the third randomly chosen point.

I think it would generally be allowable to say "pick three points", then have someone pick three points, and then say "calculate the distance between points 1&2, points 2&3, and points 1&3, and then define A and B as the two points that are farthest apart", and then proceed with the rest of the argument. But I'm not 100% sure.

Is there any reason why my argument above that the probability is 3/4 is incorrect? For that matter, is there any reason why the following argument that the probability is about 64% is incorrect? Are they ALL correct?!?

Both of these are considering the infinite plane case, not the finite area case.

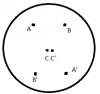
The problem is still solvable. Remember that you only need to tell which person of #1, #2, and #3 corresponds to A, B, and C -- it doesn't ask you to also solve whether the left hand or the right hand of each person signifies truth. The three yes/no questions would have to distinguish between six different states, which is (at least theoretically) possible. But you are correct: if you also need to figure out whether the left or the right hand signifies yes or no for even one of the three people, then you would have to distinguish between 6 x 2 = 12 possible states, which can't be done with three yes/no questions. That gets to the fundamental "trick" of solving the problem.

Like Bonanova, I'm also curious whether the answer you had in mind is essentially the same, or if it uses a different approach?

In that scenario (#1 = Truth, #2 = Random, #3 = Liar): Question 1: Robot #1 (Truth) gives you a White light because he can't tell how Robot #2 (Random) will answer. So you know that Robot #3 is not Random and you ask #3 the next question. Question 2: Robot #3 (Liar) gives you a Red light... it knows that Robot #1 (Truth) would answer with a "Yes" so it lies and answers "No" to produce a Red light. So you know that Robot #1 is either Truth or Liar but can't be Random, and you conclude that #2 (the Robot you haven't talked to yet) must be Random.

Well played, all, and especially Nana. It was fun being able to lie some -- it's actually sort of surprising how little lying actually takes place in Mafia so it's nice to be able to do things like claim that Araver didn't block me or that I'm Wonder Woman or that I'm Amazo. I was thinking that Nana would eventually have to out that she's not Wonder Woman and then have to deal with the fact that I had already claimed Amazo without her speaking up earlier, and then at the very least would be unlikely to be saved by the goodies. But she ended up going until the game was already decided without dropping the Wonder Woman claim and still got Phil to save her even when I thought I made a pretty good case that she can't be telling the truth about being Wonder Woman.