Birthday

The day before yesterday I was 25 and the next year I will be 28. This is true only one day in a year.
What day is my birthday?

The day before yesterday I was 25 and the next year I will be 28. This is true only one day in a year.
What day is my birthday?
A teacher thinks of two consecutive numbers between 1 and 10. The first student knows one number and the second student knows the second number. The following exchange takes place:
First: I do not know your number.
Second: Neither do I know your number.
First: Now I know.
What are the 4 solutions of this easy number puzzle?
This is definitely one of the harder number puzzles on this site.
A teacher says: I'm thinking of two natural numbers greater than 1. Try to guess what they are.
The first student knows their product and the other one knows their sum.
First: I do not know the sum.
Second: I knew that. The sum is less than 14.
First: I knew that. However, now I know the numbers.
Second: And so do I.
What were the numbers?

An easier number puzzle is as follows. Two friends are chatting:
- Peter, how old are your children?
- Well Thomas, there are three of them and the product of their ages is 36.
- That is not enough ...
- The sum of their ages is exactly the number of beers we have drunk today.
- That is still not enough.
- OK, the last thing is that my oldest child wears a green cap.
How old were each of Peter's children?
What mathematical symbol can be placed between 5 and 9, to get a number greater than 5 and smaller than 9?
Can you arrange 9 numerals - 1, 2, 3, 4, 5, 6, 7, 8 and 9 - (using each numeral just once) above and below a division line, to create a fraction equaling to 1/3 (one third)?
What 5-digit number has the following property? If we put numeral 1 in front of the number, we get a number three times smaller, than if we put the numeral 1 behind this number.
Find a 9-digit number, which you will gradually round off starting with units, then tenth, hundred etc., until you get to the last numeral, which you do not round off. The rounding alternates (up, down, up ...). After rounding off 8 times, the final number is 500000000. The original number is commensurable by 6 and 7, all the numbers from 1 to 9 are used, and after rounding four times the sum of the not rounded numerals equals 24.

Find the number if:
What is the cipher? There is more than 1 solution.
The grid below is to be filled with six numbers (3 vertical and 3 horizontal) from the given list. You can use each number more than once. After completing the number puzzle sum up all digits in the grid. This is defined as the score. What is the maximum possible score?
the grid available numbers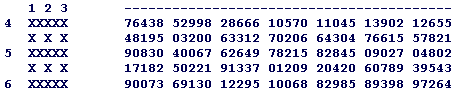
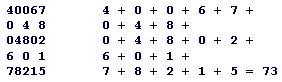
The score is 73 (of course other solutions with higher scores are possible).
Find the four-digit number designated by asterisks, given the following:
6152 +0
4182 00
5314 00
5789 +
-------------
****
Using the numerals 1, 9, 9 and 6, mathematical symbols +, -, x, :, root and brackets create the following numbers:
29, 32, 35, 38, 70, 73, 76, 77, 100 and 1000.
All the numerals must be used in the given order (each just once) and without turning upside down.
Using four sevens (7) and a one (1) create the number 100. Except the five numerals you can use the usual mathematical operations (+, -, x, :), root and brackets ().
Rectify the following equality 101 - 102 = 1 by moving just one digit.
There are infinite formulas that will fit any finite series. Try to guess the following number in each sequence (using the most simple mathematical operations, because as I mentioned, there is more than one solution for each number sequence).