Rebus Puzzles
The following word picture puzzles are pictograms that include a hidden word or a common phrase. Your task is to decipher the rebus puzzles.
For instance, on the following picture there is the first word highlighted and the hidden phrase is "first aid".

Try to find encrypted messages in the following rebus pictograms.
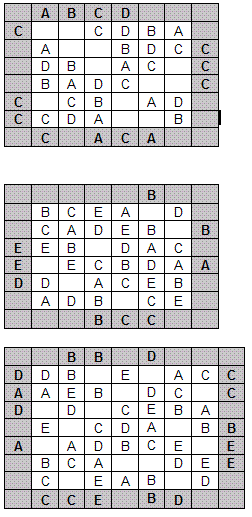
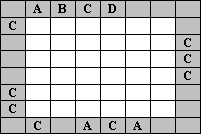
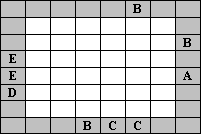
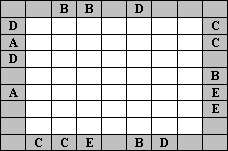
Letter Bourse Picture Puzzles
Enter the letters A, B, C, D, E once in each row and column (in the first picture just A, B, C, D). The clues outside the grid indicate which letter appears first from that direction. In the third puzzle, for example, D must be the leftmost letter in both the first and third rows, and C must be the bottommost letter in the first and second columns.
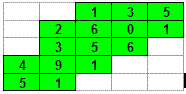
Domino Hunt
There are 28 dominos in the picture (0-0, 0-1, 0-2, ..., 6-6). Unfortunately, the edges can not be distinguished from the middle lines and it is up to you to find out where the 28 domino pieces are placed.
Where are the edges?

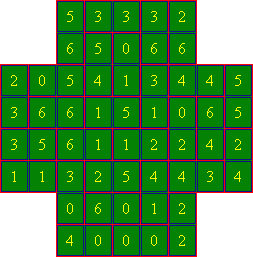
Crisscross
This is a number crossword puzzle. Enter one numeral character into each square. The clue consists of mathematical operations (e. g. "D.6 x 3" means, that the number you are looking for is three times bigger than number D.6).
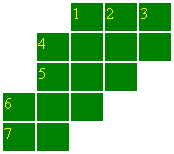
Across:
A.1 = D.6 x 3
A.4 = A.7 x A.7
A.5 = (D.3 x 7) - 1
A.6 = A.1 + A.5
A.7 = D.3
Down:
D.1 = ?
D.2 = A.7 x 6
D.3 = D.6 + 6
D.4 = A.4 - 210
D.6 = (D.2 + 9) x 1/7
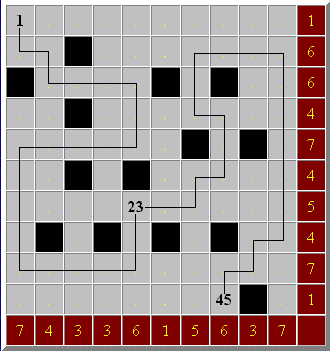
Nessie
A monster snake, 45 m long, hides under water. The picture below shows the area where the monster is hidden. Each square represents 1 meter. Parts of the snake's body are connected horizontally or vertically across the squares on the picture below. Above the surface, there is only his head (1), tail (45) and 23rd meter part of body (23). The yellow numbers on the margins show how many squares are occupied by the snake's body parts in the corresponding row or column. Black squares are stones, where the snake can't be.
So where is the snake?

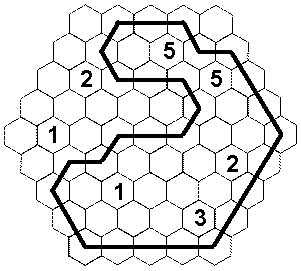
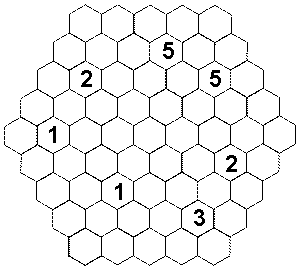
Hexagons
Find a looped path through the diagram subject to the following constraints. The path proceeds from one hexagon to an adjacent hexagon through the center of each hexagon, passes through no hexagon more than once, does not go through any numbered hexagon, and never makes a acute angle turn (i.e., a turn at a 60o angle). Each number indicates how many of the adjacent hexagons are part of the path.
Share this page with your friends