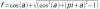Prime

There is no guaranty what weights are present/absent in your collection. The only guaranty is that each of the stones weighs a whole number of grams between 1 and 6. 12 stones each weighing 6 grams is one of the variations we must account for.

I read this one long time ago in Russian translation of one of Martin Gardner's books. One of the conditions there is that the Judge cannot possibly lie. It is an old, very interesting twist on liars' paradox. I believe the mostly accepted solution is: The proposition made by the judge is not decidable. Therefore, the condemned man may not derive any inferences from it. They could execute him on the very last day Saturday, and still it would be a surprize. Thus it turns out, the judge did not lie.

You have a dozen (12) stones weighing a whole number of grams between 1 and 6 each. You can obtain one reference weight of your choosing. What reference weight can you choose to be able to figure out the individual weights of the 12 stones using a balance device for any possibility that may exist therein? For an encore: what is the maximum weight range of stones (1 to N) that you could solve using 2 reference weights of your choice? Provided you can have as many stones as you need. I don't believe, I have solved this one myself. We could make it a community project after the first question is answered. HISTORICAL NOTE: This problem originated on Brain Den. I constructed it based on Bonanova's problem Weighty Thoughts: http://brainden.com/forum/index.php/topic/4932--/?p=84107 few years ago. Back then limited number of people participated. The solution found was for specific numbers in that problem (range 1 to 5) – not general. I'd like to give it another try.

I thought about that. But the OP states your child needs to "cut out 10 circles". Her assignment was not to "glue," "tape," "construct," or even "make" -- it was "cut out." Although, she should still get her credit and praise for creativity, if she does not blab out that a parent has done the project for her.

If I understood the statement of the problem right: 1). The hour hand changes its state from stopped to moving clockwise, or from moving to stopped every time the minute hand passes over it. 2). The minute hand continues moving in the same direction as before when it passes over the moving hour hand and reverses its direction when it passes over the stopped hour hand.

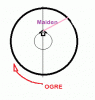
Then the problem is solved tor a straght line escape and it is the tangential line off the inner circle's perimeter. The new problem becomes how to feed the Ogre. Perhaps, if we convinced the maiden that there is such a thing as zig-zag mode, the Ogre could get his dinner after all. Although, the straight line escape, most likely is not the optimum. The optimum must be some curve dictated by Ogre's movement. To prove (or disprove) that we could let her row half way along the tangent line and then figure out new optimal path from that position.

For a straight line escape, it seems clear that the optimal angle is between the zero (straight line to the nearest point on the shore) and the tangential line escape. Past the tangential escape, maiden re-enters her inner circle going towards the Ogre causing him to change the direction. You have calculated the precise rate O:M rate (f) for the tangential escape. And it is better than the nearest point escape. However, for the other angles in between those two, calculation of maiden's trip is a bit more messy. I think this problem still has a suspense left and warrants further investigation.

It is a lot simpler than that for the zen master Ogre. The Ogre ignores where the maiden looks, where she goes, and where she intends to go. Ogre simply draws an imaginary straight line from the center of the lake, through the boat, to the shore; and heads for that spot using the shorter arch. Insofar as the optimum is concerned, it is the Ogre who determines the path -- not the maiden. The maiden reacts to Ogre's moves, not other way around. If the maiden wanders back into her inner circle r, that could make the Ogre change the direction when the boat crosses straight line drawn from the Ogre to the center of the lake. Then the young lady would be going towards Ogre rather than away from him. (Not an optimal strategy.) Presently, we are solving the sub-problem, where the maiden after leaving her inner circle goes in a straight line towards some point on the shore. We must find, that point. Bonanova suggested going off the inner circle on a tangent line. That gives a better ratio than going in a straight line to the nearest point on the shore. However, I don't believe it is the optimum. The numbers I have given in the post #23 inside the spoiler are off. But then, as everyone knows, I am siding with Ogre. Blame it on the cold, Prime. I am not convinced that tangential is optimal - it may not be enough! It's easy to overlook that r is one of the unknowns. I did overlook that r is one of the unknowns because of cold and my partiality to Ogre's cause. Still I don't see that the problem is solved even for a straight line escape. By the way, I did not see the answer by Phaze to which you referred. Is BD not displaying some of the posts to me?

It is a lot simpler than that for the zen master Ogre. The Ogre ignores where the maiden looks, where she goes, and where she intends to go. Ogre simply draws an imaginary straight line from the center of the lake, through the boat, to the shore; and heads for that spot using the shorter arch. Insofar as the optimum is concerned, it is the Ogre who determines the path -- not the maiden. The maiden reacts to Ogre's moves, not other way around. If the maiden wanders back into her inner circle r, that could make the Ogre change the direction when the boat crosses straight line drawn from the Ogre to the center of the lake. Then the young lady would be going towards Ogre rather than away from him. (Not an optimal strategy.) Presently, we are solving the sub-problem, where the maiden after leaving her inner circle goes in a straight line towards some point on the shore. We must find, that point. Bonanova suggested going off the inner circle on a tangent line. That gives a better ratio than going in a straight line to the nearest point on the shore. However, I don't believe it is the optimum. The numbers I have given in the post #23 inside the spoiler are off. But then, as everyone knows, I am siding with Ogre.

Tangential escape does not seem the optimal even for the straight line escapes. The straight line escape with a 45-degree angle seems to perform better.

I have a cold, my head is stuffed, I feel like an Ogre. I am not figuring out the differential equations to deny hungry Ogre his meal. However, here is some food for thought for those Brain Denizens who took the maiden's side. Indeed, she could go slower. Mayhap, someone will try carrying out the required calculations, make an error and give the maiden a wrong advice. To make the contest fair, the maiden should have only so much time for rowing. Having exhausted it, she falls asleep. Whereafter, the Ogre should start blowing at the boat pushing it towards the shore...

I was developing a winning strategy for the Ogre based on the inertia of the boat. But then Bonanova added an infinite acceleration.

Nice problem. Are you sure she has to row that fast? The question in the OP is: "How fast she must she be able to row..." (meaning top speed.)

The series is infinite, and the variable term thus equals zero. There are equal numbers of boys and girls on average. Bonanova is right. It's a happy ending. In each generation everyone gets his/her mate.

Nice problem.

Oops, seems I messed up again.

The number of people in the society is not specified either. I assume, there are n married couples.

To reiterate the point Bushindo has made already (post#4.) There is a difference in average distance from origin after n steps and how many steps are required on average to travel that far. The average distance includes variations where the drunkard has traveled further and then returned. On the other hand, to travel further than 1.5 steps, he must make at least 2 steps. The probability of leaving the area after one step is zero, so the first step does not add anything to the average steps; whereas it does add its full size to the average distance. One way to run a computer simulation is to make random steps until the drunkard wanders past the designated radius, tally up the steps it took for each experiment and calculate the average. That should show how many steps it takes on average to leave the area. Another way is to have n steps in each experiment, tally up the distances traveled, calculate the average. That would show the mean distance from origin after n steps.

Oops, forgot another square root. Here is the correction/addition to the previous post. Normally, I try to avoid using integrals and calculus in general. I don't like that branch of mathematics and don't believe in it. So it is entirely possible I messed up the above formulas. Besides, I have not actually figured out the Integral I used for this solution. But never mind all that. I checked few sources on the internet regarding two-dimensional random walk problem. I did not feel like submerging into the complex math presented there. Imo, those sources used insufficient justification and explanation for the formulas they use. What's interesting, in my brief examination, I did not see my concept of the average increase in distance from any given point with each step in the treatments of Random Walk in Two Dimensions. (As shown on the diagram in my previous post.) Are there any professional mathematicians here to shed light on this?

I believe this problem is about a drunk man, not an ant. He takes 1 meter step, falls, gets up makes another step in random direction, and so on. I don't see how this trip averages out to zero and returns to the same point. Clearly, it is not true for the first step. And the probatillity of getting back to the point of origin on the second step is slight. I am not sure wheter the title I used "Two Dimensional Random Walk" is the conventional name for this problem. Must check the literature, (which I never do.)