Prime

I'd like to enter the following solution and claim the minimum number of throws.

I want to be a party pooper. This one is unfair. Nice. However, as Bushindo has noticed this one may require replay for number of participants other than power of 2. So there is no ceiling on how many coin throws decide the winner. I'm trying to go for the minimum expected number of flips here. This is my best attempt so far Awesome. Same problem though – no ceiling. And it seems fair, but not in an obvious way. A proof of fairness would be nice.

If we know the average area of a randomly drawn triangle inside a unit circle, then the problem is solved. How do you find the average area of triangle? Where does 35/48Pi come from? http://mathworld.wolfram.com/DiskTrianglePicking.html But that's not solving the puzzle, that's finding an answer on the internet. I don't understand 5-tuple integrals and would have to study to verify that solution. It is educational. However, to discover something of our own, I'd look for a simpler more understandable solution.

The history of this problem as I recall it. I suggested first solving the average distance between two points inside the unit circle. Then solving the average distance from a point to a segment inside the unit circle. Thus finding the average area of triangle and ultimately solving the problem. I don't recall that anyone coming up with a solid analytical solution. Bonanova ran computer simulations providing the numeric answer and came up with analysis, which I did not quite follow at the time. There was some confusion about the 4th point inside the triangle formed by the first 3 points, versus concave quadrilateral. I belive I resolved that question this time around in the post #3 with corrections by Bushindo in post #4.

If we know the average area of a randomly drawn triangle inside a unit circle, then the problem is solved. How do you find the average area of triangle? Where does 35/48Pi come from?

Now, that question 1 is solved, I am inclined to yield the opportunity of solving question 2 to others. I think the proof is fine as it is, but I believe there are a few typos. See below Question for bonanova: about question 1- the probability that the 4th point falls within the triangle, Yes, I muddled my explanation. Of course, I meant not forming convex quad, or forming concave quad. But I did mean the point inside a triangle. Perhaps, I should have mentioned re-drawing the lines connecting the points. At any rate, my post solves the relation between question 1 and question 2. The straightforward approach with sixtuple integral seems too complex and more a numeric than analytical solution. As far as I remember, Bonanova had done numeric solution back when, by runnig computer simulations.

Since question 1 was not a part of that problem posted in 2008, let me provide a solution to that one real quick. Now, that question 1 is solved, I am inclined to yield the opportunity of solving question 2 to others.

I recall vaguely, trying to solve that problem. I seem to recall we did not come to a consensus back then. It seems like a serious math problem. And we were trying to solve only the question 2 there.

I think I misinterpreted your position. I don't think bononova and I share the same interpretation of 'uncertain', though. Let me see if we have the following positions correct The way I see it, Bonanova has made his problem statement/position 100% clear: Uncertainty is when Cole's winning chance by shooting in the air = his winning chance by shooting at Alex. The question Bonanova wants us to solve is: For what values of b (accuracy of Bobby) such situation is possible? And solved it we have: Bushindo's view of uncertainty is the same as Bonanova's: Wshoot_air(b,c) = Wshoot_at_Alex(b,c). However, there seems to be some uncertainty as to what exactly Bonanova wants us to find. Prime picks on the usage of the word uncertain. Does not believe there is any uncertainty here at all. (When chances are equal, Cole must shoot Alex, because he hates him more than he hates Bobby.) Also, Prime promotes (unsuccessfully) an alternative strategy whereby Cole shoots himself in the foot with his very first shot.

Hopefully, this solves all tiebreak situations and removes the uncertainty. Reading from the OP: Given that it [Cole's strategy] is uncertain, what can we determine regarding Bobby's shooting accuracy? From your reasoning regarding Cole's strategy, what is the answer? I agree about semantics. I think the underlying crux of the discussion is the interpretation of 'uncertain' Now Bushindo is with Bonanova insisting that Win(shooting air)=Win(shooting Alex) means uncertainty. What's wrong with my tiebreaks? A true 3-way duel indeed. But all got the same answer to the problem. I can see where my guidlines to Cole in post#4 could be misinterpreted. My intention was to help Cole avoiding computations, where possible. For if he sits down with a calculator in the middle of the duel, the other two guys may get angry and just shoot him out of turn.

That's not what paragraph 2 says in the OP. You're right. OP is corrected. I was presumptuous to teach you how to solve ... Apologies. Thanks. That brings it closer. I get a positive weight rope now, alas, not enough for the monkey and the rope together to balance the weight.

Hopefully, this solves all tiebreak situations and removes the uncertainty. Reading from the OP: Given that it [Cole's strategy] is uncertain, what can we determine regarding Bobby's shooting accuracy? From your reasoning regarding Cole's strategy, what is the answer? We are arguing semantics. To me uncertain means cannot be determined, like division by zero. I just do not see the choice between two equally good (bad) values as an uncertainty. And I have given several good ways to decide the tiebreak. I don't think it's all that important in our three way duel. I figure, Bushindo's objection was to omitting inclusion of all of the variations into the equation. I think we are in the right to do that. And after algebraic simplifications the full equations would come to the same thing. And we all use different nomenclature. (Mine is the easiest to type, although not as formal.) I found it interesting that in Bonanova's analysis, using probability of missing (q), simplifies the solution. In particular the solution of the cubic equation. I say, this duel is solved. Alternatively, shooting himself in the foot may be the best option for Cole.

Let me try and bring consensus here by wearing everyone down with a lengthy, unnecessarily tedious, and tiresome detailed solution. Outside of solving inequality, which I think is more revealing than equality, I don't see any significant difference in the results. I did use a little shortcut without giving an adequate explanation/justification for it. Therefore, I feel compelled to clarify the point where the reasoning ends and algebra begins. Hopefully, this solves all tiebreak situations and removes the uncertainty.

That's not what paragraph 2 says in the OP.

The stipulation that all 31 rectangles are “of the same size” is still a bit ambiguous. The size could be interpreted as area. If rectangles were equal that would imply they are equal in area (2 squares each) and dimensions. However, do we need a stipulation that rectangles must be alined on square boundaries? If rectangle's dimensions were specified as 1x2, then the problem would be solved by googon97 in post #5. But those rectangles could be 1/3 x 6, or 1/2 x 4. Still, it is impossible to cover up the board with 31 of those rectangles. Furthermore, can we prove that we could or could not cover the board with 31 equal area (2 squares each) rectangles of any dimensions?

It seems hard for White not to win. If Black had their own tangible threats, that could reduce the number of solutoins to the problem.

White seems to win in whichever way, provided it has the first move from that position.

Your proposal (tethering 4 ships to the 5th) is akin to increasing the mass of the 5th ship by five times while also increasing the fuel tank five times. Your solution assumes that fuel usage for the navigating ship is the same whether it is alone or whether it has 5 times the mass. In physics, as in life, there is no such thing as a free lunch. You can't carry 5 times the mass to Mars without expending extra energy. Perhaps you are thinking that the navigating ship only has to set a course for the entire fleet, so the energy usage is independent of the mass. Recall that in space, if you need to change the course, you will need to change the momentum vector of the entire fleet. That means if you want to move 1 degree to the left, for example, the navigating ship will need to provide enough thrust (energy) to move its entire mass to the left that much. Even if we allow the conservation-of-energy violation, the 5 ships still can not make it to Mars and back. From your OP, "each spaceship has a fuel capacity to allow it to fly exactly 1/4 way to Mars" and "Each spaceship must have enough fuel to return safe to the base space station". Since each tank will take you 1/4 of the way to Mars, 5 tanks are enough for 1.25 of the distance to Mars. How are your 5 ships supposed to get to Mars and get home on 5 tanks? The fuel feeds a small generator on board producing enough electricity to send a signal to Mars' Sub-Ether Tractor Beam station. The signal relays precise position, velocity, and mass of the ships. The Tractor Beam on Mars supplies all required energy and does all the work in pulling and guiding the ships towards their destination. Once arrived, the ships must bomb the Tractor Beam station, because such is their mission. You might ask, why Marsians are playing along. Because they know the ship has enough fuel only for a fraction of the distance to send the signal. It's simple.

I am uncertain, what uncertain means in this context. Cole's first shot strategy is clear. He must shoot himself in the foot thus exiting the duel with a non-fatal injury. (Hopefully, he does not miss.)

Actually, we should split the difference and go with 27.

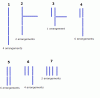
Correction: It is 10 arrangements for the variation 4. Then the answer is the same as K-man has found.

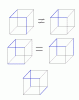
Good spacial vision exercise. Without looking at an actual model of a cube, I am not sure I got it right. Next, let's try it in 4-D.

Somehow, I see paragraph 2 differently.

I understand, it's more of a language exercise, than math.