Prime

This concept, does not apply to the question in the OP. The problem called for finding the minimum number of rolls (or dice) to get a winning bet. A winning bet is one, where your probability of winning is better than 0.5. It is not the same concept as average number of rolls (dice) required to get to the objective. A simple example: If you roll repeatedly a fair dice, then any given number, say "1", will occur on average once in six rolls. However, if I bet on "1" coming up just after 4 rolls or sooner, I am going to come out ahead. (Same as rolling 4 dice and betting that at least one of them will roll "1".) P = 1 - (5/6)4 = 0.5177 The answer to the problem as stated is like Sp and myself have found. I have another equation, which is not recursive, but encompasses all variations. It yields the same result. I'll make a separate post for it. But of course you still get a winning bet with 14.7 rolls. Your winning chance is better than 60%, but it is not the minimum number of rolls.

I like the original wording. It is fair and accurate. It does not actively mislead, rather allows solvers to mislead themselves. It could use no leading zeroes stipulation to prohibit all zero solution, but then it would simplify solving process quite a bit. The fact that some people suspected an error in the problem statement, while Bonanova remained silent on the subject served as a hint to me. The title could be “6 equations, 12 unknowns,” or even more catchy “6 against 12,” to attract more attention. Great puzzle!

Now that I took few minutes (enough to prohibit editing previous post) to study the statement of the problem closely, I find my solution (above) answers OP's requirements in full.

I found couple solutions, but not with as many digits, I'm afraid.

Can we assume, there are no leading zeroes in any of those 2-digit numbers?

Ah, I see.. Thanks, CaptainEd for clearing that up.

I can get an answer, but no simple explanation. But that should do for everyday gambling needs.

I don't see how you can achive this set of 2-side totals with 2 standard dice. If we can add any 2 sides there should be 6C2 = 15 totals. Whereas, OP lists just 12. If we only add each 2 adjacent sides, then we get a set of 12 2-side totals. However, I don't see how that set of 2-side totals is possible with standard dice. What am missing here?

If we drop (1), it's not really a puzzle. There are more than 14 men on the death row. Which means they are either prisoners of war, or this whole thing takes place in Texas. Either way most of them are innocent in all likelyhood. With such obvious signaling as turning around, they are all doomed. I would choose some more inconspicuous signal, like someone in the formation turning the toe of his left foot inside ever so slightly.

Turning around when new man enters is clearly a communication. And the OP said:

I assume, duplicate occurences of the sme word don't count. This would be a good programming exercise. I got 12 different words.

Found the ultimate mate in 9 moves.

Thanks, TSLF. I don't see how Black can get stalemate in that sequence. I could not find the 9-move variation.

Shouldn't the OP be F=1, H=2,... etc.? In the alphabet of (f, h, n, y) k=1! Why should F=1?? Please see my above explanation How is "f=3" in that counting system? The letter "f" has no straight lines. Perhaps, you meant "F=3".

Another ultimate mate position in 11 moves.

This problem should be easier for a good chess player. I only found this:

Shouldn't the OP be F=1, H=2,... etc.? In the alphabet of (f, h, n, y) k=1!

The closed form expression 1+6*2n-1 seems close, As for programming: Of course, the execution time could be reduced by storing calculated results in an array and taking them from there when available. Recursive code seems most economical and simple, but it is dangerous. For this problem, I would use non-recursive code. Modifying Bushindo's code to store results in array and do itterations instead of recursion we bring execution down to just 137 itterations: Define Array P[143]; P[-5]=P[-4]=P[-3]=P[-2]=P[-1]=0; P[0]=1; FOR N=1 TO 137 P[N]=(P[N-1]+P[N-2]+P[N-3]+P[N-4]+P[N-5]+P[N-6])/6 PRINT P[N]; (Dont' ask me what language it is in.) Execution time notwithstanding, recursive code gives rise to interesting math questions and Fibonacci like series.

I got a similar order; my table of numbers differs though.

If the crooks who have already formed 4 neat rows start turning around in their places upon the entry of the next criminal -- that should be deemed as a form of communication by the warden. If they stay put until the newcomer takes his place, he has 3/4 chance of spoiling that neat formation. If you arrange randomly, say, 16 men in 4x4 formation, no consecutive change of which way they face can guaranty thus newly formed rows' order and same colors in each row.

That is a trick question. Another math question for computer programmers is lurking in this thread. It has to do with Bushindo’s recursive code: This computer program calculates the exact probability, until it uses up the allotted precision. And it is most economical in terms of code. However, it may not be so as far as execution time is concerned. Most of the running totals are re-calculated multiple times. Function P(n) calls itself 6 times for all n > 0. The math question is: How many times the recursive function P(n) will be called for P(137)?

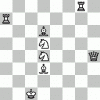
And, if I understood correctly, Black King is not allowed to capture White pieces.

That's a good puzzle. I suggest, start a new topic for it. This topic has been marked as "solved" on the first page. Some people won't even go to this page and will not see your puzzle. The wording could be: "From this position White makes regular chess moves. Black King can jump to any unattacked square. Check mate the Black King."

Yes...thats right....he should wait until the previous prisoner is standing in his raw and took his position. Nice approach. I agree tho that the warden might object. Also, wouldn't the nineteenth prisoner also need to execute this [seemingly one-time-only] ploy? I didn't mean that as one-time-only ploy I say, let them get executed.

Yes...thats right....he should wait until the previous prisoner is standing in his raw and took his position.