Prime

I was going to add the caveat that I cannot verify the usefulness of google translate. But yes, I thought all monkeys played football. Nice. Whereas one of the two Google founders was born in Moscow. You must know Russian to appreciate and fully enjoy the beauty of the translation. The first sentence of the translation actually is: The rope [to] pulley had ran up to ... (As if the rope or pulley had legs and actually ran. Hard to say which.) Working off the OP in English with some aid of Russian translation I get a very large negative weight for the rope.

The grammar in the OP contradicts that solution. Then again, what do I know. English is not my native language.

Possibly, you have found the smallest number fitting the conditions in the OP. However, a simple proof/solution does not present itself. When designing new puzzles that comes with the territory. I appreciate invention of new puzzles. It's a different process from uncovering an answer that has been found before. While playing with this problem I came up with some interesting divisibility rules, which could be used to construct riddles, or break public/private key encryption. Perhaps, this particular puzzle could be simplified by requiring two digits in the product, rather than three.

Going with the following assumptions as answers to my questions: 1. Leading zeros are allowed. 2. We work with the sum of numbers, not digits. 3. The school No. 7 is in Moscow in the vicinity of MSU (МГУ) and Vernadski Prospect. I have a different proof of the same, which gives even more insight into divisibility rules, but it would take longer to explain. We have another Divisibility puzzle going here: http://brainden.com/forum/index.php/topic/15583-more-divisibility/?p=328196]More divisibility

Do tickets include numbers with leading zeros? Do you add together all actual 6-digit numbers, or just the digits from those numbers? In which town math school No. 7 is located?

Indeed, this number is a bit smaller than the one I found. But where is the proof that it is the smallest number that meets the conditions?

The goat in the picture is about 50 yards long and 40 yards tall. I would not like to meet it in a dark alley.

Конечно ... Веревка подбежал шкив, на одном конце была обезьяна, на другом конце вес.Два оставшихся в равновесии.Вес каната было 4 унции / футбол, а в возрасте от обезьяны и мать обезьяны составил четыре года.Вес обезьяна была много фунтов, как мать обезьяны было лет, и весом весом и весом каната вместе были в полтора раза больше, поскольку вес обезьян. Вес вес превышал вес веревки, как многие фунтов, как обезьяна лет, когда мать обезьяны был вдвое старше брата обезьяны было, когда мать обезьяны был вдвое старше брата обезьяна будет, когда брат обезьяны в три раза стара, как мать обезьяны Когда мама была обезьяна была в три раза стара, как обезьяна в пункте 1. Мать обезьяны был вдвое старше обезьяна Когда мать обезьяны был наполовину стара, как обезьяна будет Когда обезьяна в три раза стара, как мать обезьяны было, когда мать обезьяны в три раза стара, как обезьяна в пункте 1. Возраст матери обезьяны превысил возраст брата обезьяны на такую ​​же сумму, как возраст брата обезьяны превысил возраст обезьяны. Какова была длина веревки? So the rope has legs and plays footbal?! And monkey's mother is a male?! And age is money?! Was it Google translation? I guess, it'll be awhile before computers can understand and translate natural language. Although it's worth noting that about the only bit translated correctly, is that very thing, which I misunderstood. The translation states, the weight of the rope together with the weight is 1.5 times the weight of the monkey, as the problem statement intended. Whereas I understood it as half weight of the monkey.

I assume, like in real life, after an introduction two people immediately become fast friends. Same thing as k-man actually. Note, it is impossible for all n people to have different number of friends, since the maximum number of people a person may know is n - 1, and with that, mininimum is 1. So at least two people must have equal number of introductions.

So the Ogre and the Maiden problem is actually a solution/approximation method for tan(x) = x + π.

Looks like the maiden gets an unfair edge here. The calculated rate does not give the Ogre his chance, unless the lake is really small and Ogre's hands are really long.

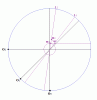
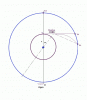
I am not disturbed. Your question points to an essential unsolved part of the problem. How should rower recalculate her path if Ogre deviates from optimal. I used the diagram to explain the idea. The picture is not to scale and very scetchy. I used large steps to make it more illustrative. The size of the lake does not matter, only the ratio of speeds does. The same concept applies if it takes the Ogre thousands of steps to run around the lake. Anyone can still work on this problem to find more efficient and creative ways for recalculation of rowers path. As well as finding how long it takes to escape, and or how far away the Ogre would end up at the landing.

I see the makings of a computer game Ogre vs. Maiden. Since both Ogre and Rower can turn on a dime and have infinite acceleration, any history of their moves means nothing. The Ogre's strategy is to spot the nearest landing point for the boat and run there along the shorter arch. However, the maiden must be given some small advantage in the speed ratio. Ogre knows that, and he is also aware that the young lady has read our blog and knows all about the optimal path. So the Ogre deviates from his optimal strategy, giving his opponent an additional advantage. But if she is so dumb as to continue on the path she started, she'll run straight into the Ogre's paws.

I see, I mixed up the adavance of the hour hand with the elapsed time for each cycle. And I calculated period incorrectly for the second part in my previous post. Still, after the corrections, I get a different answer. My hour and minute hands will meet a lot sooner. Why rejecting the occurences where the clock hands meet at 12 in a mid-cycle? I see nothing in the OP prohibiting that. In fact, the clock hands will meet again at 12 on a mid-cycle before they do so after a whole number of cycles.

This puzzle bears some logical inferences, which allow to dispense with extra complex math. Just what we all like in puzzles.

You need at least one side length among your three pieces of information for a triangle. Three angles won't do.

It seems, you have proven that the tangential straight line escape is the optimal path. I'll try to put put a simpler perspective on this whole Ogre-Maiden business using BMAD's “Dog Freedom” recent problem in this forum. It appears, there is no spiral escape. But don't tell the maiden.

I suspect, your suspicion is correct. That's the same reference weight that I found. There is a certain criteria for it. Rather than enumerating all different cases, I invite all participants to try and find cases, which would be indistinguishable with this reference weight. K-man came close to the solution and was the first to "think outside the box",

I suspect, your suspicion is correct. That's the same reference weight that I found. There is a certain criteria for it. Rather than enumerating all different cases, I invite all participants to try and find cases, which would be indistinguishable with this reference weight. K-man came close to the solution and was the first to "think outside the box",

For the part 2, you can have 2 reference weights of your choice, as many stones as you want in the weight range from 1 to N. (Must find the largest N and the 2 reference weights.) Let's solve the first part first. No tricks, no cheating, no different interpretations of the OP. If there is an ambiguity, I'll clarify it.