BMAD

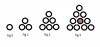
Look at the following four figures. They change in a similar pattern. Assuming the pattern continues, will the inside of the circles ever be at least double the outside count? If so, when does this occur?

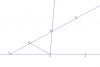
Also assume that AX is a line and AY is a line

Here is a classic puzzle: Triangle ABC and BCD are isosceles. AB = BC = DC and AY=AX. What else can you infer from this?

So optimal means minimize the sum: floors+doors+ keys. yes.

This is a nice puzzle. What is the relation of the ten floors to optimality? Is optimal fewest operations or shortest time? optimal in the sense that i want to go to the fewest floors and fewest doors and testing the fewest keys possible. Does it take time to travel between floors? Are there n elevators ? travel time is not a consideration, we could use the exercise Are you initially inside your basement office? If so can you open its door without first identifying its key and using it to get out? you start out in the basement which is unlocked. but you do need to know what unlocks this door.

Alas, the basics i miss. yes. there are 6 rooms on a floor with the exception of the basement where there is only 1. And yes, you need to find a key for the basement as well.

You were recently hired to be the head of maintenance in a mathematics building. The building has 61 doors but 60 our locked. In your office you have ten keys. Each key unlocks at least 1 door and no two keys unlock the same amount of doors nor the same door. There are ten rooms on a floor, with your office being in the basement (for technically an eleventh floor). 1. Develop an optimal strategy that will quickly tell you how many doors each key unlocks. 2. Develop an optimal strategy that will quickly tell you which door each key unlocks (if different from #1).

I posted a question similar to this one sometime ago but I thought it fun to revisit and make it a little more challenging, so here we go: You are wearing a blindfold and thick gloves. An infinite number of quarters are laid out before you on a table of infinite area. Someone tells you that 20 of these quarters are tails and the rest are heads. He says that if you can split the quarters into 2 piles where the number of tails quarters is the same in both piles, then you win all of the quarters. You are allowed to move the quarters and to flip them over, but you can never tell what state a quarter is currently in (the blindfold prevents you from seeing, and the gloves prevent you from feeling which side is heads or tails). How do you partition the quarters so that you can win them all?

good start.

64 teams are going to play in a tournament. You desire to bet your $192 savings on these teams but you know absolutely nothing about these teams so you will use a fair coin to select the team that you think will win the contest. Every correct bet doubles your money so a $1 bet awards you back your dollar plus an additional dollar and you cannot bet on two teams if they are playing each other in the same round. The tournament is a single elimination contest, hence there will be 6 rounds. Your goal from betting is to attempt to make the most money at the end of the tournament. You have two friends who proposed betting strategies: Jon says that you should bet $32 for each round evenly. So in the first round, you put $1 on each team you think will win, then in the second round $2, culminating the final round with $32 on the winning team. Eric, on the other hand, says you should bet $3 on each team in the first round, $3 on each team in the second round, and so on. If you bet on the same teams regardless on the strategy chosen, which strategy will produce the most money?

Mr. Smith works on the 13th floor of a 15 floor building. The only elevator moves continuously through floors 1, 2, . . . , 15, 14, . . . , 2, 1, 2, . . . , except that it stops on a floor on which the button has been pressed. Assume that time spent loading and unloading passengers is very small compared to the travelling time. Mr. Smith complains that at 5 pm, when he wants to go home, the elevator almost always goes up when it stops on his floor. What is the explanation? Now assume that the building has n elevators, which move independently. Compute the proportion of time the first elevator on Mr. Smith’s floor moves up.

(sqrt(9)*sqrt(9))/9

your logic is sound and the last of your explanation is on the correct track

A galaxy consists of three planets, each of them moving along a straight line with its own constant speed. If the centers of all three planets happen to lie on a straight line (some kind of eclipse) the inhabitants of each planet go nuts (they cannot see their two neighbor planets all at once), start talking about the end of the world, and the stock market crashes. Show that there will be no more than two such market crashes on each of these planets.

A sequence of natural numbers is determined by the following formula, A[n+1] = a[n] + f(n) Where f(n) is the product of digits in a[n]. Is there an a[1] such that the above sequence is unbounded?

Four black cows and three brown cows give as much milk in five days as three black cows and five brown cows give in four days. Which kind of cow provides more milk, black or brown?

Carter fenced in a rectangular plot of land and then divided it into two halves by putting another fence along the main diagonal. This diagonal fence measured 41 metres exactly. Martindale also fenced in a rectangular plot of land in a similar way (including the diagonal fence) but his rectangle was one-third greater in area than Carter's plot and used less fencing. In both plots all the the dimensions (lengths, widths and diagonals) were a whole number of metres. How much more fencing did Carter use than Martindale?

Assume there is a one-lane highway with traffic uniformly moving at 65 mph. An accident occurs, causing cars to stop on the highway. After the accident is cleared off the road, the traffic jam persists. Does the traffic jam persist at the same spot where the accident occurred? Why or why not?

Here are a few http://en.m.wikipedia.org/wiki/Criticism_of_Christianity

A high quality rubber band is fastened and hung from a horizontal pole with a cannonball at its end. Two facing ladybugs are crawling along this rubber band toward each other. From their respective starting positions (8 cm apart), each small beetle crawls toward the other at a speed of 1 cm per second. However, in the length of time each beetle crawls 1 cm, the cannonball, thanks to the force of gravity, stretches the rubber band an additional 8 cm. Will the poor ladybugs ever meet? And, if yes, when? If not, why?!

Find the value of h.

All the circles and semi-circle are tangent to each other and are inscribed in a square. The 3 small circles are the same size, with radius r. R is the radius of the red circle. Prove that r = 3R/8

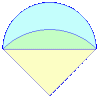
The blue crescent is made up of a semicircle and a quarter circle (of a larger circle). If the width of the figure (diameter of the semicircle) is 1, what is the area of the crescent?

Little Picard Theorem: If a function f : C → C is entire and non-constant, then the set of values that f(z) assumes is either the whole complex plane or the plane minus a single point. from wikipedia: http://en.wikipedia.org/wiki/Picard_theorem