BMAD

i think the rate would be the same in terms of average growth

Sheesh people. 17 then

this is what i have as well.

hmmm... okay assume there are 20 skittles.

I agree that you found the 'missed assumption' by the farmer but i calculated a different answer. Someone please verify.

nope. that assumption was safely given.

help me understand this sentence: "Each person receives an anonymous list of 99 numbers representing everyone else's numbers but not her own." it reads to me, that a person would have a list of numbers that excludes the number they have. Let's look at a smaller problem with 10 people and integers between 1 and 10 inclusive. Suppose the 10 numbers given out were 1, 2, 2, 2, 3, 6, 7, 8, 8, and 10. Further suppose that Mary has been assigned the number 2 (not known to her, of course). Then Mary would be given the list 1, 2, 2, 3, 6, 7, 8, 8, and 10. One of the 2s would be missing -- one that represents what she has been assigned. This is the intent of that sentence. ah ha brilliant. i get it now.

help me understand this sentence: "Each person receives an anonymous list of 99 numbers representing everyone else's numbers but not her own." it reads to me, that a person would have a list of numbers that excludes the number they have.

The image was just to show what I meant by how to line them up. Calculate for any N.

My pack of skittles comes in five flavors, grape, lemon, green apple, orange, and strawberry (odd that they don't have the cherry blue flavor found in the UK but alas). Assume that my pack had the following proportion of flavors 2.5 lemon, 2 orange, 1.5 grape, 1.5 green, 1 strawberry. If i were to pour my skittles on the table and line them up in an offset two row pattern (so that at most, a single skittle touches four skittles [see image]. What are the chances that two skittles of the same color won't touch?

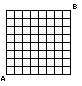
Consider an N x N grid. Denote one corner as point A, and the opposite corner as point B. George is walking from A to B, and Lennie is walking from B to A. All paths are equally likely, as long as they follow the grid and never move away from the destination. (Hence George's path can never move down or left, and Lennie's path can never move up or right.) What is the probability that George and Lennie collide? If George runs and thus moves three times faster than Lennie, what is the probability of collision?

Freddie the farmer has a paddock that he uses to graze his stock of cows. Each cow eats the same amount of grass each day, regardless of how many other cows are in the paddock and irrespective of the amount of grass left in the paddock. In an experiment, Freddie puts 6 cows into the paddock and he finds out it takes 3 days for them to eat all the grass. These 6 cows are then taken out of the paddock to allow the grass to grow back. After the grass has been allowed to grow back to the original amount, Freddie then puts 3 cows into the paddock. This time he finds that it takes 7 days for the 3 cows to eat all the grass in the paddock. Freddie is puzzled that the cows took this long and consults a mathematician. Freddie said "Geez mate, I dunno why me cows took that long to eat me paddock." Marvin the mathematician replies "Well Freddie, tell me what assumptions you made." Freddie replies "Well mate, maybe me cows got sick or somethin', cos I reckon that me 3 cows should have taken 6 days to eat me paddock, not 7 days! " Marvin Replies, "I doubt that very much Freddie!" After a while Marvin does some calculations and reveals that Freddie had overlooked an important assumption. What was the assumption Freddie had overlooked? Using Marvin's assumption, how long would a single cow take to eat the same paddock?

I have 19 coins in my pocket which total $1.00. You have 15 coins in yours that also total $1.00. Who has a greater probability of randomly pulling a dime out of their pocket?

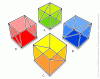
In the illustration four flat cube-like shapes are shown. Their patterns are drawn with bold black lines. Which of them can you draw without taking your pencil off the paper or going along the same line twice? Which of them can't be drawn in this way? *found this interesting gem online.

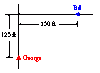
George is driving 100 ft/sec toward an intersection. He looks to his right, and sees Bill, driving 30 ft/sec toward the same intersection. George foolishly slams on his brakes. If he had kept going 100 ft/sec, he would have been through the intersection long before Bill got there. At the instant that he slams on his brakes, the center of George's car is 125 ft from the intersection, and the center of Bill's car is 150 ft from the intersection. George's brakes give his car an acceleration of -30 ft/sec/sec. Bill never changes his speed. Each car is 13 ft long and 7 ft wide. Will there be a collision?

Would the solution change if we consider that the initial mark is from a curved end and not square? like the picture below:

Suppose you have a single sheet of an 81/2" x 11" paper. Your task is to draw the longest continuous line possible using an EXPO marker that has infinite ink. The line can curve but it cannot be picked up off the paper or overlap and of your previously drawn line. Since you are drawing a line with a marker, your line has a defined width. For the sake of argument, presume your line width is 1 inch. What is the longest possible line that can be drawn?

Should we be digging the inside of the shape?

In drawing lowercase English letters a through z uniformly at random, the expected time till you see willywilly is 26^10 + 26^5. In drawing numerals over 0-9 uniformly at random, the expected time till you see 1231231 is 10^7 + 10^4 + 10. In flipping a fair coin, the expected time till you see HTHTTHT is 2^7 + 2^2. See a pattern? Find it ... then prove it.

While willywutang was trying to be clever by using only two condoms to satisfy three women, increased friction between overlapped latex layers produces a tear and a dangerous accident! He then becomes very worried about having contracted an STD, especially since one of the women was 'looked like she could have an STD. Although a random person has only probability 0.001 of having an STD, poor willywutang just can't sleep over those odds. Frantically he hustles to the nearest drugstore, to purchase the ACME All-Purpose STD Checker. The packaging boasts a 0.93 correctness probability. That is, if the user has an STD, the ACME STD Checker will return positive 93% of the time; if the user does not have an STD, it will return negative 93% of the time. Willywutang returns home and uses the checker in his bathroom. To his dismay, the results are positive. Assuming that willywutang's promiscuity on average is identical to that of a randomly chosen person, what is the probability that willywutang has STDs?

Starting with 0 dollars, you repeatedly flip a fair coin, earning $1 each time heads appears, and losing $1 each time tails appears. When your net cash reaches either A or -B, you stop gambling. As a function of A and B, compute the expected number of flips until the game stops. Now consider the unstopped version of this process, in which you gamble indefinitely regardless of your current profit or debt. Prove that the expected time till your net cash is +$1 is infinite. Likewise, the expected time till your net cash is -$1 is also infinite. note that one of these two events must occur upon the first coin flip!

So are we saying only one case is true?

Here is a classic exercise: Which of the following are true and why? 0.99999..... < 1 0.99999..... = 1 0.99999..... > 1