BMAD

Will that work in three dimensions? Good point. Is that the least amount?

An athlete wants to compete in a race. The race requires the athlete to swim to set buoy and back and then trek up a hillside. Practicing the athlete noticed that it takes her 3 hours to make it to the buoy and back. Going back for her was much faster (2 miles per hour less). Going up hill, she was able to run in some parts and walk in others. She ran 3 miles in 20 minutes and walked an average of .08 miles per minute. If she swam for 8 miles and walked for 10 minutes, what was her average speed throughout the exercise?

Will that work in three dimensions?

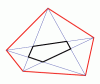
Joining every vertex of a convex pentagon to every other vertex forms three nested figures: the original outer pentagon an inner pentagon a five-pointed star between them Suppose the perimeters of these three figures are all primes; show that the three primes’ sum is at least 20.

A Bright Star is a sphere, not just a point, that emits light in all directions from every point on its surface. A Dark Star is an opaque sphere whose dull black surface reflects no light. Dark Stars come in all sizes. Your assignment is to get and position a few of them around a given Bright Star in such a way as will absorb all its light, thus rendering it invisible from afar in every direction. What is the minimum number of Dark Stars required to carry out this task, and why?

**Risking the chastisement of repeating another forum question** Samwise Gamgee has a square plot of land, each side being 1 unit. One day, Sam finds out that the dark Lord Sauron has a telephone line that he uses to speak with a traitor amongst the hobbits. Gandalf informs him that the telephone line runs in a straight line parallel to the ground and passes beneath the square plot of land, but he does not know its location. Sam decides to dig up around the perimeter of his land to discover the telephone line, but Gandalf says it is not necessary to dig around the entire length of 4 units. Sam brightens up, and says "I know what you mean. I can just dig 3 sides and still discover it. For even if the phone line runs along the fourth side, I will still detect it at the end points ! " Gandalf shakes his head. "No, Sam. You are on the right track, but you can do better than that." What solution does Gandalf have in mind for the optimum length of the "digging curve" ?

yes. you can ask any question about another person.

Call a set of cubes incongruent if they all have different side lengths. Prove that it is impossible to exactly fill a rectangular box with incongruent cubes. Note: The phrase "exactly fill" means that there is no space in the box which is not occupied by a cube, and that the cubes themselves should be packed together to form the shape of the rectangular box that envelops them.

The southeast puzzle is played on a semi-infinite chessboard, starting at its northwest (top left) corner. There are three rules: In the starting position, one piece is placed in the northwest-most square, as shown in (a). It is not permitted for more than one piece to be on any given square. At each step, you remove one piece from the board, and replace it with two pieces, one in the square immediately to the East, and one in the the square immediately to the South, as illustrated in (b). Every such step increases the number of pieces on the board by one. After move (b) has been made, either piece may be selected for the next move. © shows the outcome of moving the lower piece. At the next move, either the lowest piece or the middle piece of the three may be selected; the uppermost piece may not be selected, since that would violate rule 2. At move (d) we have selected the middle piece. Now any of the pieces may be moved, except for the leftmost piece. Puzzle: Is it possible to obtain a position in which all of the ten squares closest to the northwest corner, marked in the rightmost figure (z), are empty?

Here is the story of three unhappy people: Angelica, Bernardo, and Cameron. Angelica and Cameron have been friends since childhood. Cameron is hopelessly in love with Angelica, but Angelica has always thought of Cameron as "just a friend". During high school, a new boy, Bernardo, moves into the area. Bernardo immediately catches the attention of Angelica, who falls head-over-heels for him. However, Bernardo is not interested in women--he is strongly attracted to Cameron. Cameron, of course, is jealous of Bernardo, because he has stolen Angelica's love away. Angelica is angry at Cameron, because she feels that Bernardo's lack of attention to her is Cameron's fault. Bernardo is jealous of Angelica, who recieves all of Cameron's attention. What are these three to do? (this is a rhetorical question--there is no need to answer it) One day, you meet them, all together in a chat room. They are all using nicknames: Uberkewl, Vaxxipaxx, and Willywutang (in no particular order). Because they are so jealous and screwed-up, each of them will only answer a question truthfully only if: one of your last two questions was to their sweetheart, and your last question wasn't to the person with whom they are upset. Otherwise, they will answer spitefully--giving you the answer that will confuse you the most. Your task is to figure out who is who. Is it possible? If so, how many questions might you have to ask? And of course you cannot ask them for their name, gender, or where they are from.

Thank you for clarifying

There is a flaw in this strategy. Since the prisoners are chosen at random, the first person can visit the room all 99 times and toggle the switch off and not have 100 of the other prisoners still make it. Resulting in the death of the group. But your answer is closer to mine. Just need a little revision.

"Here's the deal. You give me $10. Then I will deal four cards (from a regular 52 card deck), chosen randomly, face down. You get to look at #1 first and decide whether to keep it. If not, look at #2 and decide whether to keep that one. If not look at #3, and decide. If you don't take that, then #4 is your choice. If your chosen value is n, I will pay you $n. Then we can reshuffle the entire deck, you give me another $10, and we can play again, and again, and again." "Hmmm....I need a good strategy to beat you at this game, but I think I can do it." Help the second player out with a strategy that will win. Note that the cards all have face value with the following exceptions: Ace=1, Jack = 11, Queen = 12, and King = 13.

alice sends different partial messages to a bunch of different receivers. by partial, we mean that one message by itself doesn't convey any meaningful information. let us denote the set of receivers as R. the messages are designed such that if any n receivers get together, they can somehow pool their partial messages together to get a meaningful message -- alice's intended message. however, if any n-1 or less receivers get together, they can't reconstruct anything meaningful whatsoever. n < |R|. what kind of messages are being sent by alice, and what mathematical function do the receivers apply on their pooled partial data to determine the intended message?

You have an infinite cache of cigarettes. What is the maximum number of cigarettes you can place on a table so that every cigarette touches every other cigarette? (You can't bend the cigarettes.)

Four ghostly galleons – call them E, F, G and H, – sail on a ghostly sea so foggy that visibility is nearly zero. Each pursues its course steadily, changing neither its speed nor heading. G collides with H amidships; but since they are ghostly galleons they pass through each other with no damage nor change in course. As they part, H’s captain hears G’s say “Damnation! That’s our third collision this night!” A little while later, F runs into H amidships with the same effect (none) and H’s captain hears the same outburst from F’s. What can H’s captain do to avoid a third collision and yet reach his original destination, whatever it may be, and why will doing that succeed?

You have an empty room, and a group of people waiting outside the room. At each step, you may either get one person into the room, or get one out. Can you make subsequent steps, so that every possible combination of people is achieved exactly once?

100 prisoners are imprisoned in solitary cells. Each cell is windowless and soundproof. There's a central living room with one light bulb; the bulb is initially off. No prisoner can see the light bulb from his or her own cell. Each day, the warden picks a prisoner equally at random, and that prisoner visits the central living room; at the end of the day the prisoner is returned to his cell. While in the living room, the prisoner can toggle the bulb if he or she wishes. Also, the prisoner has the option of asserting the claim that all 100 prisoners have been to the living room. If this assertion is false (that is, some prisoners still haven't been to the living room), all 100 prisoners will be shot for their stupidity. However, if it is indeed true, all prisoners are set free and inducted into MENSA, since the world can always use more smart people. Thus, the assertion should only be made if the prisoner is 100% certain of its validity. Before this whole procedure begins, the prisoners are allowed to get together in the courtyard to discuss a plan. What is the optimal plan they can agree on, so that eventually, someone will make a correct assertion?

In the city of Funkytown, the following facts are true: No two inhabitants have exactly the same number of hairs. No inhabitant has exactly 483,207 hairs. There are more inhabitants than there are hairs on the head of any one inhabitant. What is the largest possible number of inhabitants of Funkytown?

I found this one online. Enjoy! What was the last move made?

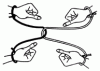
In a cliche effort to illustrate the importance of teamwork-oriented problem solving, the Boss has chained Dilbert to Carol The Secretary via wire wrapped around their wrists, as shown in the following snapshot: The goal is for Dilbert and Carol to unlink themselves from each other; considering what a horrible woman Carol is, Dilbert wouldn't have it any other way. The wire is unbreakable, and as much as Dilbert would like to saw off Carol's limbs, that's against company policy. How can Dilbert and Carol get away from each other?

The absolute value of a real number is defined as its numerical value without regard for sign. So, for example, abs(2) = abs(−2) = 2. The maximum of two real numbers is defined as the numerically bigger of the two. For example, max(2, −3) = max(2, 2) = 2. Express: abs in terms of max max in terms of abs