-
Posts
6975 -
Joined
-
Last visited
-
Days Won
66
Content Type
Profiles
Forums
Events
Gallery
Blogs
Everything posted by bonanova
-
Adam, Bill and Charlie stood in a line with Adam in front and Charlie at the rear. Charlie could thus see both Adam and Bill, Bill could see Adam, but Adam could not see either Bill or Charlie.Their teacher brought out a box containing three red hats and two blue hats. She placed on each boy's head a hat from the box and asked them to name the color of the hat they were wearing. Although all three responded to the question, only Adam knew the color of his hat. And now so do you.
-
Assuming "first" means lowest-numbered,
-

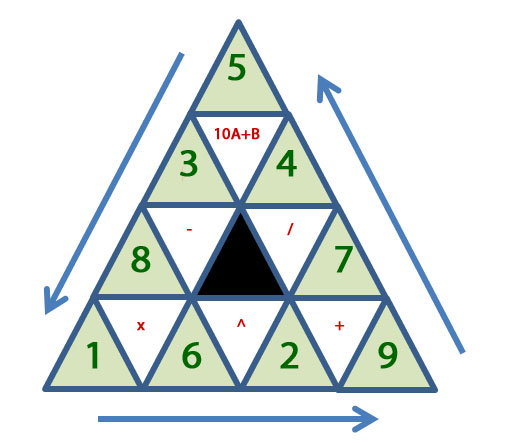
Arrange numbers and operators to the magic triangle
bonanova replied to jasen's question in New Logic/Math Puzzles
-
Nope. He is a "real" Bill, though. Just a little older than Clinton. Keep in mind that Picket's post is on the right track.
-
You can use the Search feature here to see whether a puzzle might have been already posted. Mouse over Activity tab and click on Search. A version of Monty Hall has in fact been posted here, although with enough different terminology it's hard to find. Either way, a member might know of a previous post and simply direct discussion to it. Regarding usefulness, puzzles are usually posted without the solution. This permits members to post their responses to your puzzle. When you feel it has been solved you can click the check mark (upper left corner of their post) to so indicate. If it's not solved after some time has passed you might want to post a clue (putting the clue into a spoiler.) You can put anything you like into a spoiler so it's not visible unless a member chooses to see it. Simply highlight the part of your post to be hidden and click on the eye icon and then submit your post.
-
Hi. That's a standard puzzle and you gave what I think is the best short answer
-
Inspired by FUZZY's recent puzzle Suppose abcd is the normal decimal representation of a number: abcd = (1000a)+(100b)+(10c)+c. The digital sum of a number is defined as a+b+c+d. Are there numbers for which the product of its digital sum and its reversal is the original number? For example, the digital sum of 12345 is 15. Its reversal is 51. 15x51 is 765, 12345 is not equal ti 765, So 12345 is not a solution. Hint: 81 is a solution, as is 1. Are there others?
-

Arrange numbers and operators to the magic triangle
bonanova replied to jasen's question in New Logic/Math Puzzles
Clarification? Each variable {A B C D E F G H I} can be used only once. I now assume, but it's not clear, that each operator {+ - x / ^ 10A+B]} can be used only once, making (9!)(6!) cases. I started allowing any operator to be used in each white triangle. -
Post away (spoilered) then ... Good job.
-
I spent way too much time trying to figure out the calculus ban. Like there a catch and it should be obvious at some point. If there was a catch I didn't see it.
-
Not bad. Wrong Bill, though. Who Bill is comes from somehow decoding the message.
-
Since there are active solvers, you may want to hold off with the solution. It's your call, of course. Another approach would be to drop a clue now and then (in a spoiler.) It's really a great puzzle, and it would be a notable accomplishment to be the first solver.
-
Here's an equation that's easy to analyze with a little insight. It's not original with me, I ran across it yesterday. (I'll provide attribution after it's solved.) x3 - y3 = 217 Does this equation have integer solutions (pairs of {x, y} integers)? If not, prove there are none; if so, find as many as you can.
-
-
@FUZZY Thalia is correct. My description of the sum is ambiguous.
-

Interesting 3x3 table, to form a numbers of unique prime numbers
bonanova replied to jasen's question in New Logic/Math Puzzles
First thoughts -

How fast can you solve these logical puzzles
bonanova replied to ammar97's question in New Logic/Math Puzzles
Hi ammar97 and welcome to the Den. The first puzzle is a standard liar-truth teller puzzle. This is the most basic of them and has been posted here in the past. There are ways to make the answer more complicated and it's a great way to think logically to solve puzzles of this type. (Suppose one of the persons randomly tells the truth, and so on.) You can actually search the site, using keywords, to see if a puzzle has been posted already. (Click the Activity tab and choose Search.) The second puzzle is less well known, and the solution comes with nice "aha!" moment. The third puzzle belongs to a broad genre of bridge-crossing puzzles. I found yours very interesting. Easy to analyze but counter intuitive to solve. There are only a few possibilities, but the answer lies well hidden among them. Thanks again for posting these puzzles, and feel free to post others, that you either write yourself or find on the Web. But here's a hint: If a published puzzle comes with a solution, then instead of linking to it, you could give it here in your own words (without the solution.) That way we won't have access to the solution until someone here solves it. Thanks again. -
Yikes! Really? It's 24 times more likely for a 3 to be drawn 5th than to be drawn 1st?
-
I like phaze's solution. I would add just a tweak, as described in the second spoiler. Recap: Tweak.
-
You are on the right track.
-
So you're a writer, Bill. Care to share some of your work? Sure. Here are a few bits of it: FF?
-
It would be more fun if there were five of us in a room working on it together. I've been distracted by other things lately but still interested.
-
First thoughts (that are consistent with a better result than in the 3-person example):
-
With a nod to jasen's recent and interesting puzzle, A traveler happened upon a village of huts, laid out as the circles in the picture below. The village's mayor explained to the traveler that the family living in each of the huts had an eldest son whose age was unique within the village. (No two eldest sons had the same age.) How interesting, replied the traveler. Tell me this: of all the male children here, what is the age of the very oldest? The mayor thought for a moment and replied, well I guess I could tell you that none of them are yet of voting age (21), and I guess you might be interested to hear that there are no gaps in their collective ages. But all of that wouldn't be enough information. I think it would be better for you to just knock on all the doors and ask. I don't have time for that, replied the traveler, and I'm really not that interested. Well, here's an interesting thing about our village, replied the mayor. You may have noticed, our huts are laid out so that many rows of 3, 4, or 5 huts cut across the entire village. Just ask at the huts along any of those rows. Add the ages that you hear, and divide the sum by two. That way you will learn the age of the oldest son in the village. And now, without knocking on any doors, you can learn it too.
-
I've brought this up with site management to have replies ordered chronologically. I think that's the order now. It's confusing otherwise.