bonanova

I think only at the North Pole this could happen. Or on a non-spinning globe. See Coriolis Force. In real life, a ball hit up in the air by a bat has great spin, and follows a curved path. In an idealized sense, with no wind resistance, and in an inertial frame of reference, a ball could go straight up and straight down. But the thing that makes this an interesting question (earth's rotation) also prevents that in general from happening. Rotation is acceleration, and it introduces forces (centrifugal and Coriolis) in addition to gravity. Over short distances and small times, their effect is small.

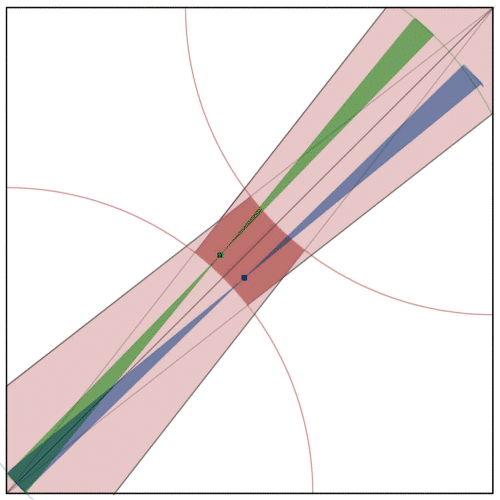
Simulation shows the probability to be 0.75. This corresponds to 100% intersection if the needles align with opposite diagonals and 50% if the align with the same diagonal. Here is a figure that suggests how this comes about: We chose here a needle length of about 1.26. A simple construction shows (light red) the area where a needle of that length could land and (dark red) the region that its center point can occupy. The center point of a green needle landed on the green dot. The green bow-tie is the region the needle can occupy with its center fixed at the dot. The blue dot is a reflection in the diagonal, and the blue bow tie is the region the mirror image of the green needle can occupy. Note the coincidence of the lower left boundaries of the bow-ties. As the green needle moves through its allowable positions in a CW motion, the blue needle does the same in a CCW motion. During exactly 1/2 of that motion the two needles intersect. During the other 1/2 they do not. This is only a suggestive proof. The bow-ties can take different locations for different landing points. In some cases the blue and green needles never intersect, in others they always intersect and in still others they intersect for fractions of their motion that differ from 1/2. All the cases average out to 1/2.

Greetings, Prof. T. Great to hear from you. The lion does start from the center, sadly for the tamer. The prevailing thought is for the lion to maintain the tamer's azimuth (his radius is shorter) and inch his way outward. By maintaining his azimuth, never leading nor lagging, the lion does not permit the tamer to gain advantage by reversing his direction. Although, since he can do so instantaneously, neither would the tamer lose advantage.

First thoughts:

It turns out to rational. When the two sticks lie close to the opposite diagonals they always intersect, when they're near the same diagonal they intersect with a very simple probability that I think can be proved geometrically

Good thinking. Let's add the condition that the lion and tamer are point objects. Can they coincide? Also, could the lion reduce the radius of his circle to that of the lion and maintain any angular separation he might at some point have obtained? (Your solution prohibits this, but suppose the lion made one misstep and just for a moment he lagged the angle of the tamer.) This question has an amusing answer.

Hi and welcome Chandra. Let's add the condition that the tamer (and the lion) can change/reverse directions instantaneously. Tamer can switch from CW to CCW at his pleasure.

If a lion and his tamer can run at precisely the same speed without tiring, would the tamer be safe inside the lion's circular cage? Assume the lion sits on a stool at the center of the cage as the tamer enters though a door on the perimeter of the cage. You can also neglect the size of their bodies. i.e. consider the lion and tamer as points.

Eeeeww!

The puzzle is interesting, especially for those who are into number theory. Last week I looked at this puzzle and decided I would not be able to find the connection among the numbers. So I searched OEIS out of curiosity. For some reason I didn't find it. (Strange.) Next I Googled the numbers themselves, and that turned up the football reference. <moderator hat on> I agree with Mike's sentiments. The Forum is for solving puzzles; it's not an Internet scavenger hunt. If you can't solve it, say so and maybe start a (spoilered) group effort. Or ask the OP for a clue. The spoiler function permits multiple users to have a go at solving a puzzle. So solutions belong there. (Even funny ones about football.) <moderator hat off>

I'll bet this is not the answer you're looking for, but it does qualify as a remarkable matchup:

Good one. But I can't identify all of the movies, either.

Assuming that they bought

In this puzzle, limits can lead us astray.

In the case of 80 mph the fly, Ferrari and truck all meet on the fly's first and only collision. The OP asks the fly to move to the truck, back to the Ferrari, back to the truck and finally back to the Ferrari. Then, "upon returning from the second trip," the three collide. The 80 mph case has them colliding upon reaching the truck for the first and only time.

Yes. Sorry I didn't make that clear. In reply to your answer,

I think those equations describe the conditions described in the OP. But I don't think there is a solution that satisfies the OP. Maybe that is just what you are saying. But I don't think it's the fault of the equations; it's the claim in the OP that the three all collide at the conclusion of the second round trip of the fly. That just can't happen if all three have constant speeds. Consider the situation at time1 + time2 + time3, when the fly has hit the truck for the second time. The fly completes his trip by returning to the Ferrari. But it doing so it must perform an impossible task. (1) It must fly back to the Ferrari at a speed that is greater than the speed of the truck (it's at least the speed of the Ferrari), but (2) it must arrive at the same time that the truck arrives. That is not possible. The fly will arrive at the Ferrari before the truck does.

Here's a simulation without actually writing the program:

I thought so at first. But simulation shows it doesn't get that high. So long as L is strictly less than sqrt(2) the probability is not close to unity.

The problem is a paradox of sorts. At all times the fly is flying *away* from one of the vehicles. So the vehicles *can't* collide with each other during any part of the fly's journey! Yet of course the vehicles *do* collide in finite time. And they *do* collide, at the same time, with the fly. That's why the fly must make an infinite number of trips. After any finite number of fly-trips, the vehicles are a calculable distance apart.

Inspired by BMAD's Pickup Sticks puzzle, I ask the following related question. Into a unit square you drop two needles (having negligible width) of length L. (0 < L < sqrt(2)). Consider the probability p( L ) that they will intersect. A moment's thought reveals that the probability approaches zero as L approaches zero. p( L ) is a strictly increasing function and approaches a limit as L approaches sqrt (2). What is the maximum value of p( L )? Clue

After re-reading the problem, I'd agree with Baskaran. In fact,

Getting this one started,

I don't have an answer yet, but here is how I would attack the problem