-
Posts
1398 -
Joined
-
Last visited
-
Days Won
14
Content Type
Profiles
Forums
Events
Gallery
Blogs
Everything posted by CaptainEd
-
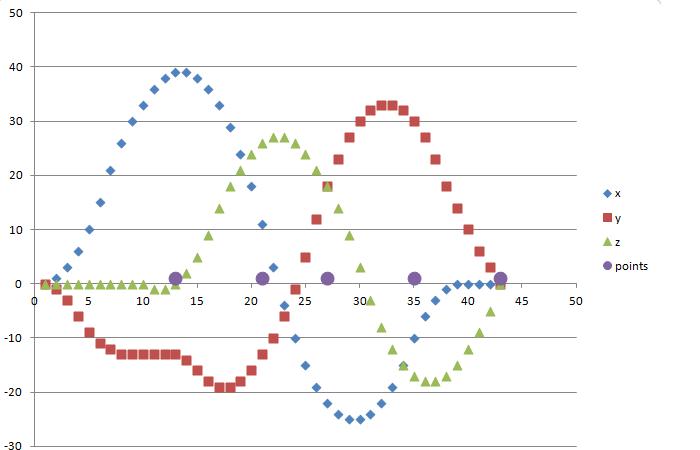
For what it's worth, here is a chart of the x, y, and z values in my recent 42 move solution. Plotting them this way made it a little easier to look for regions that wanted to be optimized. I think...
-
I agree, guessing the best order is hard. I've published answers with two different orders (turns out, I didn't even identify when points were near-misses to marks, sorry...), and I have no idea yet what the optimal is. I have a theoretical thought that sometimes, you'd turn around before or after hitting a mark, so as to get high enough velocity to get to the next one, which is why I imagine that it might be good for a line segment to pass through the mark. However, as I said, it takes some programming that I have not had time to do, so I can't show an optimized path that benefits from that. Molly Mae, have you got below 42 yet?
-
Morningstar, Molly Mae's answer to this seemed to me to say that each line segment has to pass through the cube no further than 1 in any dimension from the target point. I didnt quite get the statement about having to hit both min and max on a dimension. My answers so far have actually ended a line segment within the cube, because the Excel spreadsheet formulas I'm using to help me keep honest look dauntingly more complicated if I try to code a line-segment-intersects-a-cube function. I have the feeling that would save some more steps, though. Molly Mae, this is interesting. doing a manual search of this space is tricky. The addition of the third dimension is good, and your diabolically pathological choices of locations is very well done! It feels like every pair of points is far apart, and every triad of points requires severe acceleration/deceleration. Great job! Not done yet...
-
Lovely! "Passing through" a sphere means which?: (a) a move ends on a sphere center or one of its 6 neighbors (b) at least one of those 7 points lies on the line segment of a move © something more complicated about the line and the volume surrounding the sphere center... (d) other Also, it appears that the origin itself is the 5th mark, and presumably is to be passed through in the same way? What fun!
-
I think I'm clear on the rules, but let me play back a couple of details: Merchant rolls, chooses a direction (high or low). If you bet in that direction, and roll a number further in that direction, you get +50%; if you roll same total, it's a draw, you roll total in opposite direction, you get -50%. If you bet in opposite direction, and roll a number in your direction, you get +100%, if you roll same total, it's a draw, you roll total in same direction, you get 0%. Is this true?
-
The spectre of 20 aces in sequence is definitely a worst case scenario. I think your answer is similar to phillip1882's, namely to divide the cards among all the players. I'll bet you folks are right. Phillip goes a bit further, by actually dealing (ie. separating) the cards to the piles, and I think that addresses your worst case scenario. I like the answers I've got. I'm going to advise dealing piles for all players. Not so clear how many rounds are necessary. If someone has some empirical or theoretical evidence telling how many rounds, I'd love to know it. But I already have benefited a lot from your help. Thank you all!
-
I fear that my sloppy use of language has done some damage. By a "round" of shuffling, I meant that all players shuffle a while, then they all pass a fraction of their deck to the next player, simultaneously. So, I would think of 3.37 rounds as being 3.37 times when they all pass.
-
Let me make sure I understand your method. Here's my paraphrase: divide the deck into n slabs, one per player. each player deals his/her slab into 4 piles (by "deals", I assume you mean deals a card to each pile in turn, until all the cards are gone) [i realize you suggested dealing somewhat randomly, but I doubt that is necessary--dealing individual cards to different piles sounds powerful in separating the same-denomination runs] each player distributes the piles to the 4 players (including self) Then each player shuffles the cards in the 4 piles they now have. And that's it. Or do we do this more than once? If doing this merely once does a good job, you're going to have a lot of friends at our house!
-
EventHorizon, certainly more than a little flaw in the OP--what do I mean by randomized? In this game, color and suit don't matter, only denomination. So randomization should result in a uniform distribution of each denomination in the deck. I realize this is still rather vague, sorry, but it's a clue. Phillip1882, since my question focused on the concern about mixing the cards from one person with those of the next, I like your suggestion very much--your proposal separates contiguous cards across all the players immediately, in one (or each) passing round. As an aside, for those who aren't familiar with Hand and Foot, the need to separate the cards is manifest in several of the pre-play activities. For one thing, after all players shuffled and passed, etc., ALL players deal, and they each deal two hands (of 13 cards). Then they pass them to their left and right neighbors (in two-hand, they pass one hand and keep the other).. Then the remaining undealt cards are put into two draw piles, and each person's turn starts by drawing one card from each draw pile. I'm liking your discussions, folks, keep those cards and letters coming...
-
The card game Hand and Foot requires one more deck than the number of players. Assume four people are playing, thus there are five decks of 54 cards each (2 jokers and 4 each of A,2,3,4,5,6,7,8,9,10,J,Q,K). The result of a round of play is a discard pile that is EXTREMELY non-random, with many contiguous strings of identically denominated cards. So, after a round of play, all players shuffle the cards. In fact, shuffling takes place in rounds. In one round, everybody shuffles a bunch of cards (in the example above, about 65 cards per player) several times, and then finally passes half the cards to the person at the right. Let's not worry about how many times they have to shuffle in order to "randomize" their bunch of cards. My question is: How many ROUNDS of shuffling does it take to randomize the cards, if we assume that they are able to randomize the cards in their bunch? Subsidiary question: what fraction of cards should be passed? That is, is it optimal to pass half the cards, or is there a better fraction. I don't have an answer to this question. I do know that we get tired of shuffling...
-
Curr3nt, I think itachi-san hit the right interpretation: "same score" does not mean "same total score", but "same pair of team scores". Then there is no conflict between a 7-4 and a 6-5 game.
-
Ah! Those look more plausible. I think the editing threshold is based on amount of time since first creation, rather than attempt-based, but I'm not sure. I make a lot of mistakes in my proofs, etc., and I so I have run into the editing threshold several times.
-
Bendigi, why do items 5-9 all have the same square? Also, my Excel shows a different square for 83647, 6996820609 rather than 2147483647
-
What fun! I love the argument that the ants' positions move independent of the actual ant identities. BUT... Let's refer to a specific point O as an admittedly arbitrary Origin. The locations have increasing labels, going clockwise. let's refer to times with distance labels. That is, if an ant is at location x, facing O, we could say that, after time x, the ant has reached O. And let "e" be "epsilon", a tiny amount. Now, arrange the ants as follows: R is at O - e facing CW. In other words, after e time units, R will be at O. the Bs are located at O+e, O+3e, ..., O+25e, all facing CCW. We can think of them as 13 blind mice. GO! At time e, R and B1 meet at O, and reverse direction. Now R is the "image" of B1. After about 13e, R will be leading the other 12 blind mice CCW, with B13 acting as the image of R, moving CW at location 13e. Since the ring is 10 meters in circumference, halfway is 5. At time e + 5, R and B13 will meet at location O+5. R will bounce, and start moving CW again, but will hit B2 at e + 5 + e, and bounce again. R will arrive back at location O+5 at time 5 + 3e, moving CCW. To get back home (O - e), R has to travel more than 5, but he has less than 5 units of time remaining. So, here is a layout that appears to fail--R does not get back home, someone else gets to R's home. If this is right, then I think exagorazo's insight comes into play: the pattern of CW and CCW ants may affect whether R acts as his own image or not.
-
I'm with exagorazo--if there were three ants, the R going CW and the two B going CCW, I think the R does not get home. I realize the OP has an even number of ants, but the Superprismatic argument does not seem to depend on the parity of the number of ants. So we wonder (exagorazo and I) whether the argument is really as strong as he suggests.
-
Yes, that solution is shockingly direct, curr3nt! Good job! What a relief!
-
I see, EventHorizon, you've shown me that the entry and exit rays are NOT counted twice, so we get to include them completely, rather than divided by two. So an entry and exit ray passes through an extra cell, adding one to the total, and they also don't get double counted, adding 8 to the total. So my estimated upper bound should have been 18 * 4 + 9 * 2 = 90. I'm not disputing that 87.5 is a more accurate bound. After all, my approximation imposed no further constraints about non-touching mirrors. As to the discussion about interior blocks, my intuition (as you said, NOT a proof) is that, aside from the possibility of connecting edges that couldn't have been connected, an interior block REMOVES up to 2 units from a path. So, I would say that a solution involving 17 edge cells and 3 interior cells could have a pathlength no greater than 84.
-
I sure don't FEEL close! By the way, there's a LOT more symmetry--the sequence appears to be a Hamiltonian circuit around a 2x2x2x2 hypercube. But I'm still missing a couple of fundamentals. 1) Perhaps we are to add one or two dimensions (egad, maybe 4 more dimensions!) 2) But his sequence always moves to a new dimension before finishing the old ones. However, this sequence has now completely filled the 2x2x2x2 without starting into new ones. 3) and I have no idea how 1-4 relate to a-d. If we see them as hexadecimal numbers, the gap between 4 and A is not a convenient one, I could be more comfortable (still clueless, but more comfortable) if a-d had been c-f. This is very interesting wolfgang, thanks for the workout...still working...