bonanova

Nana, I think this one was previously posted, although quite a while ago and perhaps before the time of most current Denizens. And since it's one of the better puzzles of its type and well worth the solve, people may want to give it another shot. For those who do, two things need to be assumed: [1] that one of the house owners does in fact have fish as a pet. [2] that "first" in the sense of Clue 9 means "leftmost" in the sense of Clue 4. With those assumptions the clues give an unambiguous solution.

The idea that three is the fewest convex vertices is nice. So far, y-san's approach gives the tightest upper bound.

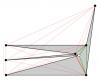
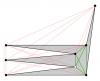
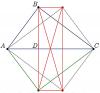
NaNa claimed enough real estate to include everything. DeGe's kite was slightly under-sized. k-man had it, but was still typing when witzar hit the Post button witzar by a nose! Good job everyone.

No. It should be included, but only once. The two triangles (the original and its mirror image) partially overlap, making a four-sided figure with vertices at (6,5) (8,-3) (10,5) and a point that is the intersection of lines segments from (6,5) to (9,1) and from (10,5) to (7,1). We want the area of that four-sided figure.

Confirm.

That is the area of a rectangle that contains all the vertices: x in [6, 10] and y in [-3, 5]. The area we need is less than that.

A triangle with vertices (6,5), (8,-3) and (9,1) is reflected about the line x = 8 to create a second, overlapping triangle with vertices at (10,5), (8,-3) and (7,1). What is their combined area?

The sequence S1, S2, S3, ... , S10 has the property that every term after the second is the sum of the previous two. That is, Sn = Sn-2 + Sn-1 for n > 2. Suppose that S9 = 110 and S7 = 42. What is S4?

Your answer will surely work, but it is not the smallest number that will always suffice. If you like, try drawing some 2p-gons, where p is 2 or 3 or 4, that are not convex. Also, consider the fact that a triangle is always convex.

You are given a plane n-gon having no intersecting sides. That is, each segment of the perimeter has interior points on one side and exterior points on the other. We wish to illuminate the interior of the n-gon in its entirety by placing lamps at various points in its interior. Clearly, if the n-gon is convex, one lamp will suffice. Concave points, however, may cast shadows in some interior regions. Since life here in the Den is never simple, we ask about the general case: To illuminate the interior of a simple n-gon, what is the smallest number of lamps that will always suffice? Does the answer change if we require the lamps to be placed at vertices?

[spoiler='Looks like']Five.

Annual Percentage Rate could be interest.

What is nen? What are Necrophiliac's nen abilities? What is APR -- or is that obvious? If Gon loses RPS, his target learns Gon's identity?

Holding my nose and jumping into the pool... Chairman: Y-san Roster: 1) Phil1882 2) Framm18 3) Flamebirde 4) bonanova (that's with a lower case b) 5) 6) 7) Back-ups: A) B) C) What is nen? What are Necrophiliac's nen abilities? What is APR -- or is that obvious? If Gon loses RPS, his target learns Gon's identity?

I'm in, either way.

Here is the solution I had in mind, and k-man found it.

I'm not sure how either. But it may lead to a divide and conquer kind of simplification, which seems to be needed. I'd be interested to know what you come up with.

DeGe, sorry for the delay in answering. I think your right triangle A1B1C2 will have sides of 4, 6 and sqrt(52). That is, A1C2 will be irrational. But did I get your construction right?

Problems like this one are amenable to brute force computation. Assume the answer is n. Take all the sets of clues that have only n-2 cells filled in. Show that all of them permit at least two solutions. That approach fails here because of size. (1016 sets of clues). So a better discussion point would be: How would you go about a getting reduction in size that would make it tractable? Which permits me to comment that I think the best puzzles are much more about methods than about answers. Basically, the difference between Aha! and Google.

plasmid should get the solve. I only arranged his examples in symmetric pairs.

How about an iPhone with Internet access to BrainDen? Seriously, I don't have a good suggestion for what you describe, other than perhaps to listen and take good notes in class, and actually converse with friends when you have that opportunity. Or converse with other Denizens here. Good luck.

Hi Adam, and welcome to the Den. I've looked at your problem and will give it a shot when I get a chance. Thanks for not posting commercial links here. Have a look at some of the unsolved user puzzles and see what you can do with them. Hope you enjoy your time here.

Ah, ok. I had Fram as Zero b/c of his "here's what I know" post. I thought that unless he made up / guessed a scenario that detailed, it would have had to be revealed to him. Agree about the complexity, and with Kika's "not always as things appear" last words.

Sudoku is a commonly played game where the digits 1-9 are placed in a 9x9 array. The rules prohibit duplicate entries in rows, columns and the nine 3x3 sub-arrays. Of course there is an astronomical number of solutions to that problem. Now, any self-respecting Sudoku puzzle has a unique solution. And to bring about a unique solution, some of the 81 cells come initially filled in. One can imagine that the simplest Sudoku puzzle would have 80 cells -- all but one -- already filled in. It would only take a glance at the 8 digits already in its row, column or 3x3 array to solve the problem. And in general, the fewer cells that are filled in, the more difficult it is to find the unique solution. So the question we ask is this: If we want to make a Sudoku puzzle difficult simply by reducing the number of initially specified cells, how many cells would have to be initially specified to still insure a unique solution?

Hi BMAD, Hint, to keep ( c ) from turning into © you can insert spaces, or use [c] as a substitute. Are there others? (a) (b) © (d) (e) (f) (g) (h) (i) (j) (k) (l) (m) (n) (o) (p) (q) ® (s) (t) (u) (v) (w) (x) (y) (z) ( c ) ( r )