bonanova

You are correct. But where shall the cut be positioned? Probably four. One for each side

Good question. Not similar. Not congruent. Just equal area (viewed from top) any shape.

Meanderings.

A man walking home takes a shortcut through a train tunnel. A quarter of the way in, he hears a train whistle behind him. The tunnel is not wide enough for the man to escape being hit by the train, so he must either turn back, or go forward, at his top speed of 20 mph. Either way he will escape, but by the slimmest of margins. How fast is the train moving? All correct solutions will be accepted. The coveted bonanova Gold Star will be awarded for a solution that can be explained in words only, without equations or algebra. (e.g. without saying, "Let T be the speed of the train and D be the distance of the train from the tunnel, then t = D/T is the time that the man has in order to ..." etc. )

You are to cut rectangular cake into two pieces of equal size, but a rectangular piece of the cake has already been removed. Your cut must be a single straight cut. (Because the cake is frosted, a horizontal cut won't work. One piece won't have any frosting.) How would you do it? Assume the cake has constant thickness, so the problem is the same as cutting a rectangular piece of paper with a rectangular portion already removed.

I'm confused about the ratios.

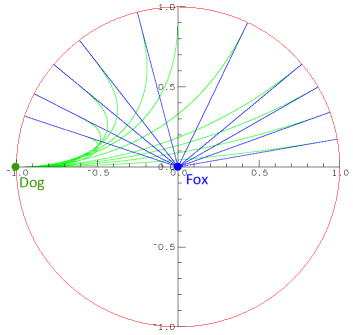
@plasmid, That's an interesting conjecture - that the lion would catch the tamer iff x=0 (in your notation.) A while back, on another computer whose drive crashed, I simulated the 45-degree case (of a dog chasing a fox, I think, but that doesn't matter) and I don't think the fox was caught. I don't recall finding an angle where there was a capture. I think I'll re-write the program. It's not hard to simulate the chase, and you can get arbitrarily close to the exact solution by decreasing the time increment. ----- OK, I searched images the site has stored from previous postings. I found this one, showing a (blue) fox starting from the origin and following various radial paths. A (green) dog starts from (-1, 0) and traces the (green) pursuit paths. The figure does not seem to indicate whether there was a capture. Note this is not the original lion vs tamer situation -- the red circle is not a cage. In fact, it may have been a modified ogre-maiden situation where the red circle denotes a successful escape for the fox.

Of course you're right. I needlessly put the chords on the same side of center.

Hi Anthony, Do you envision having solvers come up with a single answer? That is, there is one particular virus, one particular set of <x> possible compounds, one particular value <y> for the number of slots, and therefore one particular ordered set of <y> compounds that will kill the virus? If so, then just give us values for <x> and <y> and we can work on it here. Or, will there be many instances of virii, with differing numbers for <x> and <y>, to be solved? If so, then what you need is an algorithm for generating clues. Or an algorithm for determining when a sufficient amount of random historical testing has been done to determine the 100% cure.

The conclusion that they must be parallel?

No embarrassment needed. It's not simple math. you can Google "pursuit curves" to get an idea. Simulations are the best answer in a lot of cases. Here's something to think about. If the tamer runs straight away along their joining line, he (obviously) keeps his full distance from the lion. Now we know that if he runs at right angles to his vector from the lion, the separation shrinks to 1/2. This suggests that if he runs at some acute angle to his lion vector (partially towards the lion) the distance would shrink to exactly zero. I don't know, and now I wonder, what angle that would be. Possibly 45 degrees?

Right, CaptainEd, middle does not imply equidistant, and your answer is correct..

In a previous puzzle we asked whether a lion can catch his tamer if both are contained by a circular cage and ran at the same top speed. Considering the radius of the cage to be r, the lion begins at the center and the tamer at some point on the edge of the cage. We now remove the cage. Assume the tamer begins running in a direction perpendicular to the direction of the lion and continues a straight-line course. Further, assume the lion follows a "curve of pursuit." That is, the lion's bearing is always in the direction of the tamer. After a long time, their two paths will become collinear, and the lion will trail the tamer by a certain distance. What is that distance. Again, consider the lion and tamer as points.

Three asteroids are traveling in a gravity-less region of space. At time t = t1 they occupy collinear positions. At a later time t = t2 their positions are also collinear. The asteroid in the middle at t1 is also in the middle at t2. Will the asteroids always be collinear? Assume the asteroids are light enough, and distant enough, that their mutual gravitational attraction is negligible.

I don't know how to do without calc or trig ... interesting puzzle

If mating is random, a male (female) could mate with their mother (father). How is that % calculated? Or (a) it doesn't matter because it's >10%, or (b) must citizens mate only with those of their own generation, thus prohibiting aunts, uncles, cousins of differing generations, etc. Actually the more I think of it, probably ANY relation closer than 2nd cousins (common great grandparents) will not bear offspring. Can we just make that simplifying assumption?

This is an intriguing problem that i find myself mulling over in my mind, I have the same questions that DejMar raises, plus some others. Does every male mate mate exactly once every day with a random female? Do the original ten citizens live for exactly 4 days? How is percentage relationship reckoned? For example: siblings=100%; cousins=50%; 2nd cousins=25%; father-daughter=50%? Just guessing here. Does "sustain" require only that after 7 days at least one citizen is living?

Seems like

First thoughts

Good catch. It couldn't have been that easy. The additional paths number because

Hi wiseabel, and welcome to the Den. So clearly there are several ways in which these numbers are similar and, equally clearly, we're to look for something beyond the fact they are integers. Three are odd, and a different group of three are prime. Three of the four contiguous pairs are descending. Only one of the digits (1) repeats among the numbers. At first glance, I don't see a common similarity, but I'll give it some more thought perhaps in a later post. Thanks for submitting a puzzle!

Looks like because