bonanova

All good ideas. What happened is a little more out of the box, tho. I suggest reading the OP carefully and don't constrain your answer unnecessarily. But by that I don't mean the wording is tricky. @CaptainEd, You're correct one one point: @Raphael lane, @Thalia, that's an interesting slant. To clarify,

In one Summer Olympic Games a single participant won both the silver and bronze medals for a single event. How could that be possible?

From your last comment this can't be right but it's all I can think of

Which is close (enough) to

From your post, 963 is the median and 968 is the mode. The expected value is the mean. My simulations also give a median of 963, but the noise didn't permit an accurate value of mode. My mean value is in the vicinity of 961.x Simulations for different size decks gave a result that I did not expect. The bigger the deck was, the higher the fraction of the top card in the left pile was: 10 cards -> ~6.5 52 cards -> ~43.6 = Queen of clubs 100 cards -> ~88.03 1000 cards -> ~961.3 After some though I think this makes sense. For a deck of N cards, the mean value of the cards in the left pile is N/3 and the mean of the right pile is 2N/3. Those values are independent of N. But we should expect the spread of the values in each pile to increase with N. I suspect the limit of the largest card in the left pile is N itself as N -> infinity. It's hard to imagine, that is, that the limit would be bounded away from N.

Since we're baring our code, here is the APL code for the 3bd-case:

Words can be added to the picture to create a proof. The notion, suggested by one of the writers quoted above, that an optical illusion turns the proof itself into an illusion is specious. The proof would go as follows.

Nice. Closed form would probably be ugly.

This is one of my fav puzzles. If you want one final clue: Otherwise, read on: It's from Peter Winkler's book "Mathematical Puzzles, A Connoisseur's Collection." Its answer constitutes a "proof without words."

Oh my. Such a pretty puzzle and still no proof? Final clue:

You answered the question correctly; I'm not sure which part of it you're questioning. It's probably the fact that

What I got, too. I think doing the actual calculation is very much harder than for two people.

plainglazed noted that the investigator measures the entire time interval between buses; k-man was first to hit on the crux of the correct analysis (getting the mark); and plasmid beautifully and comprehensively reminded me again that I used to know how to evaluate integrals. Uh, rephrase. Has reminded me that I no longer recall how to evaluate integrals ... without looking them up. Kudos to all. The idea is that Here's the quick analysis provided by the Quora article I mentioned at the top: The idea is similar to BMAD's puzzles about random arcs on a circle enclosing a particular point. The arcs correspond to interval times and the point corresponds to the sampling process.E[T]=∑ttp(t)=10260+35260+10260+5260≈25

Just read this on Quora and it seemed interesting enough to ask: How many unique ways are there to make change for a US dollar? 293

I guess the puzzle asks how the randomly sampled wait times could be significantly greater than the actual average wait time of 15 minutes.

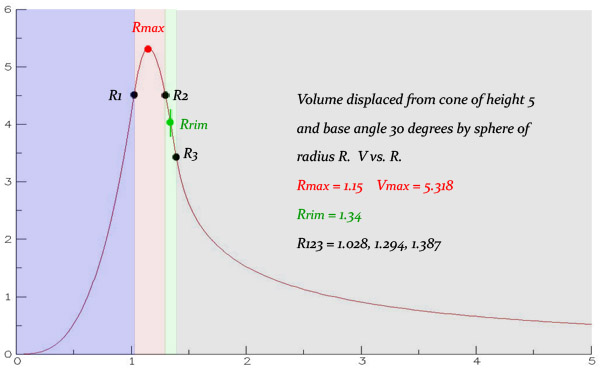
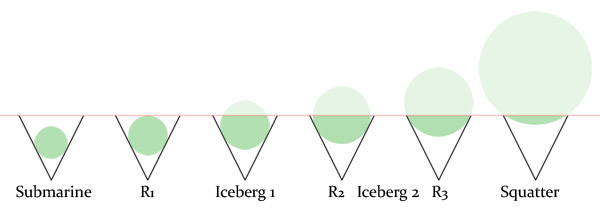
If a sphere is dropped into a conical goblet filled with water, there is a sphere radius for which a maximal fraction of water is displaced (spilled) from the goblet. The maximum fraction varies with the base angle of the goblet. What is the greatest value of the maximum fraction? For what base angle does it occur?

Most puzzle addicts know by now that in a room containing just 23 random people there is a 50% chance that at least two of them share a birthday. But how many would there have to be to have an even chance that at least three share a birthday?

If I hold an illuminated sphere in front of a screen, it casts a circular shadow whose area is exactly 1/4 of the area of the sphere. Now let the object have protrusions, but remain convex -- as for example a tetrahedron. Will its "bumpiness" create a shadow area that is greater than 1/4 of its surface area, on average?

It's a very simple result. Buddyboy3000 was close ...

Good point. You're right that my statement refers to the case at hand. How general it is now is clearly questionable. I had in mind to calculate R2 and Rmax vs θ for a unit height cone, but left it undone for some personal matters at home. I imagine one or the other of the iceberg regions always contains Rmax, and for one particular value of θ, Rmax would just equal to R2.

The puzzle seems to have been solved, although BMAD might be asking for a specific solution, tailored to the given coin bias. If so, the bias should be determined as a prerequisite to the finding that solution. In that vein, when we compare two numbers, "more," (as in five more) generally implies adding, while "times," (as in 5 times) generally implies multiplying. Thus 75 is 50 more than 25. So we would say the probability of heads is 50% more than that of tails when the probability of heads is 75%. It's clearer, when % is not used for probabilities, to say 0.75 is 0.50 more than 0.25. It's muddier otherwise, since "%", once the question "% of what?" has been answered, generally implies multiplication. My reservation with CaptainEd's suggestion is that it is biased toward tails. The first result is likely heads; the result that changes it is likely tails.

Clue:

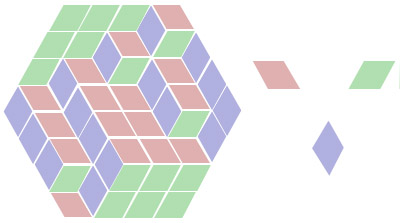
Is a tiling possible that does not have equal representation of colors? Edit: OP asks: Prove that every tiling of the hexagon contains equal numbers of red, green and blue diamonds.

Logophobic found R1 and R2 and found the radius of greatest displacement with numerical methods. plasmid rederived the formula for a sperical cap and got a closed form solution for the 60-degree goblet. Logophobic then found the closed form solution for the 30-degree goblet. Apologies to plasmid for not clarifying the issue of goblet angle. Since Logophobic was the first solver, I'll give his post the mark. I came across this puzzle some years ago and decided it would be fun to solve it again. I didn't remember what angle was given for the goblet so I used a fairly narrow one. As plasmid points out, 60 degrees might have made it an easier task. Here's my solution of the puzzle

A regular hexagon is sliced into congruent equilateral triangles and then tiled with diamond shapes made of two triangles in three different orientations. Prove that every tiling of the hexagon contains equal numbers of red, green and blue diamonds.