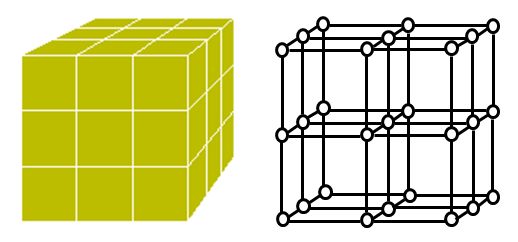
Suppose 27 identical cubical chunks of cheese are piled together to form a cubical stack, as illustrated below. What is the maximum number of these cheese chunks through which a mouse of negligible size could munch before exiting the stack, assuming that the mouse always travels along the grid of 27 straight lines that pass through the centers of the chunks parallel or perpendicular to their sides, always makes a 90 degree turn at the center of each chunk it enters, and never enters any chunk more than once?
Question
rocdocmac
Hopefully this one has not appeared before...
Suppose 27 identical cubical chunks of cheese are piled together to form a cubical stack, as illustrated below. What is the maximum number of these cheese chunks through which a mouse of negligible size could munch before exiting the stack, assuming that the mouse always travels along the grid of 27 straight lines that pass through the centers of the chunks parallel or perpendicular to their sides, always makes a 90 degree turn at the center of each chunk it enters, and never enters any chunk more than once?
Edited by rocdocmacFigures didn't show!
Link to comment
Share on other sites
14 answers to this question
Recommended Posts
Join the conversation
You can post now and register later. If you have an account, sign in now to post with your account.