-
Posts
852 -
Joined
-
Last visited
-
Days Won
25
Content Type
Profiles
Forums
Events
Gallery
Blogs
Everything posted by TimeSpaceLightForce
-

Teeter -Totter
TimeSpaceLightForce replied to TimeSpaceLightForce's question in New Logic/Math Puzzles
-
1) How can the you balance the see-saw by exchanging any 2 kids position 4 times? 2) Which twin weighs different from others?
-
Great solving job!
-
[]------A--------------------------------------------------------------------------------- / \ _|_ [H] [H] [G] [ I ] [W] [ I ] [E] [E] [ T ] [ T ] [ W ] [G] ========================================v========================================= How will the crates above can be balanced on both sides of the ship using the crane to swap any 2 of them 5 times?
-
-

Sticks Kinematics
TimeSpaceLightForce replied to TimeSpaceLightForce's question in New Logic/Math Puzzles
Relative to the long stick, i.e. when an a fly is on the long stick it would see both the short stick and the yard stick rotating at the same speed. -
A yard stick was cut on 1 foot mark so that the other 2 footer stick cut can be placed on top of another yardstick to make it roll or pivot on its ends and middle around (above and below) the yardstick clockwise. While the 1 footer stick was placed on top of 2 footer stick to make it roll around it counterclockwise without touching the fixed yardstick. Starting at position shown and same 1 RPM motion, how long will it take for the sticks to knock the ball down?
-

June 2013 POM - * not solved * - Enter Exit Code
TimeSpaceLightForce replied to TimeSpaceLightForce's question in New Logic/Math Puzzles
the display says ... [P] [O] [M] [W] [O] [W] [T] [N] [X] -

An Antiquated Math Challenge
TimeSpaceLightForce replied to Yoruichi-san's question in New Logic/Math Puzzles
-

June 2013 POM - * not solved * - Enter Exit Code
TimeSpaceLightForce replied to TimeSpaceLightForce's question in New Logic/Math Puzzles
-

June 2013 POM - * not solved * - Enter Exit Code
TimeSpaceLightForce replied to TimeSpaceLightForce's question in New Logic/Math Puzzles
...Nothing happens, Progress:50% -

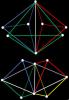
Isosceles triangle inscribed in red-blue-green circle
TimeSpaceLightForce replied to witzar's question in New Logic/Math Puzzles
Nice puzzle. I figured the number of points should be odd, to make other points become candidate pairs once a vertex was chosen. I was able to confirm 9 points were not enough. I fell asleep exploring 11. Nice solve as well! -
Not in highlight, it is right! APPLE Not in sight, it just might!
-

Isosceles triangle inscribed in red-blue-green circle
TimeSpaceLightForce replied to witzar's question in New Logic/Math Puzzles
-

Da Vinci's Secret Letter
TimeSpaceLightForce replied to TimeSpaceLightForce's question in New Logic/Math Puzzles
-

Isosceles triangle inscribed in red-blue-green circle
TimeSpaceLightForce replied to witzar's question in New Logic/Math Puzzles
-

Isosceles triangle inscribed in red-blue circle
TimeSpaceLightForce replied to witzar's question in New Logic/Math Puzzles
-
How many questions that can be answered by True or False (w/o mentioning any of the letters) will it take to determine the secret letter inside Da Vinci's letter box? Q W E R T Y U I O P A S D F G H J K L Z X C V B N M
-
-
-
This is not true. Pick a random real number from interval [0,100]. What is the probability that picked number is not 7? Clearly 100%. Does it follow, that picking 7 is impossible or that number 7 does not exists? Clearly not. Divide unit circle into 6 equal arcs. Paint those arc blue and green alternately (so that six end points of the arcs are painted alternately too). You have an "impossible" blue-green circle. In fact you can take just one arc (1/6 of circle) and paint it any way you want. Then for each point P of the arc take a regular hexagon H inscribed in the unit circle such that P is a vertex of H, and paint the other 5 vertices of H alternately (regarding color of P). Again you have an impossible blue-green circle. "Divide unit circle into 6 equal arcs. Paint those arc blue and green alternately (so that six end points of the arcs are painted alternately too)." Then "all red centered circles" are painted that way. Making 0 deg-green, 60 deg-blue. But the points are alternated so 30 deg is green (even). Therefore all ends of 60 deg arcs is two colored while all ends of 30 deg arcs is one colored. If two red centered circles , where one has twice the radius of the other intersects at P2 and P1 ... P2 r1 60deg 30 deg r2 P1 are P1 and P2 same colored or not ? or 1 is colored cyan?
-
This is not true.
-
-
An interstellar military base is protectes inside by 4 heavily Armed Frigates in a tetrahedral formation also serving as sentries and can produce a triangular force shield. An allied battleship , also protected by 4 Frigates arrived to join them in prepartion for the massive enemy offensive. Initial Two units (convention: Nos. represents depth of single frigate) 2 2 1 2 2 1 2 2 A) The Supply fleet arrived to join them. As a the commander, how will you reposition the 8 Frigates to cover the 3 units in symmetrical formation with same spatial territory (volume)? Answer for :Three units defense 2 2 2 x x 2 1,3 2 x 2 2 2 B) The Resource Gatherer unit arrived to join them. How will you reposition the 8 Frigates to cover the 4 units ? C) The Builder Brigade unit arrived to join them. How will you reposition the 8 Frigates to cover the 5 units ? D) The Fighter Dock arrived to join them. How will you reposition the 8 Frigates to cover the 6 units ? E) The Training Center arrived to join them. How will you reposition the 8 Frigates to cover the 7 units ? F) The Main Powerhouse arrived to join them. How will you reposition the 8 Frigates to cover the 8 units ? G) If more units will arrive to join in the strategic structure. How many can the 8 Frigates cover in maximum?