araver
-
Posts
1976 -
Joined
-
Last visited
-
Days Won
5
Content Type
Profiles
Forums
Events
Gallery
Blogs
Everything posted by araver
-
Confirming LOUISIANA WKTJBPCM Guess I needed to eat something since it was early morning for me
-
KENTUCKY UUEKAMFO KANSAS UASMCPUA ILLINOIS NKNOKTJN 30 down, 21 to go
-
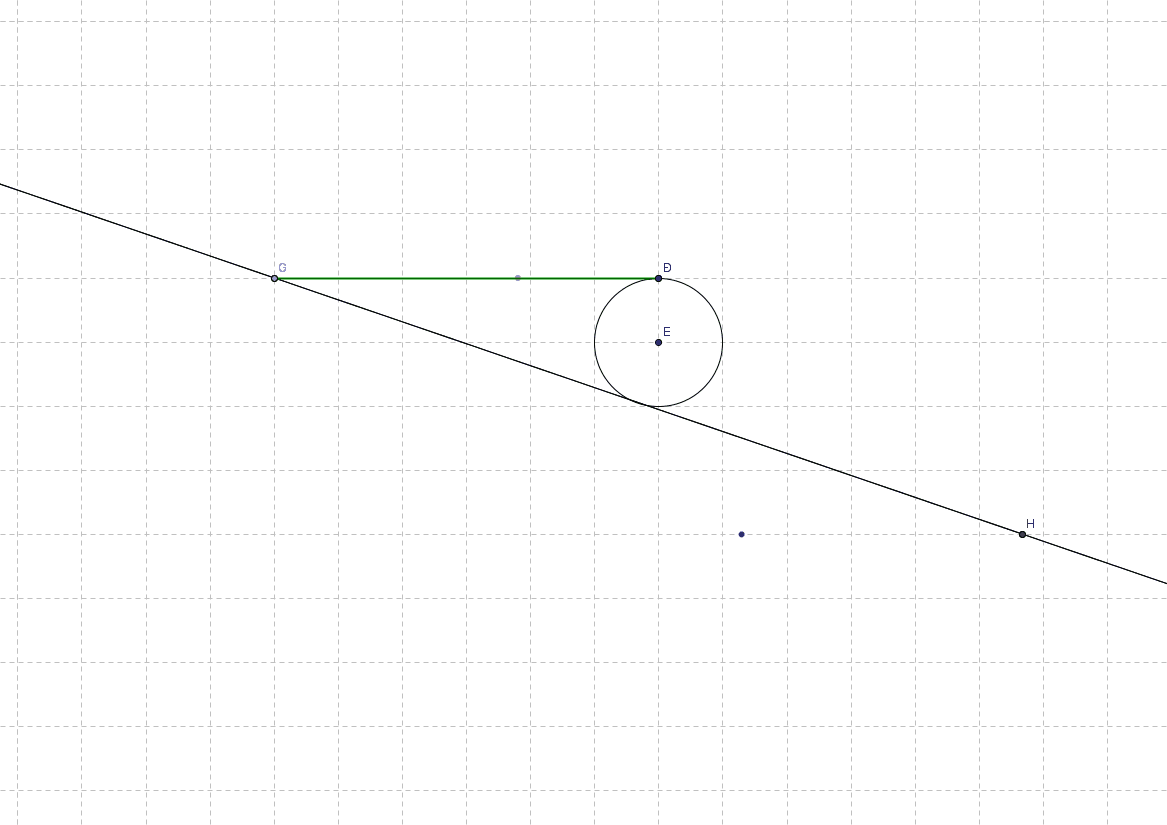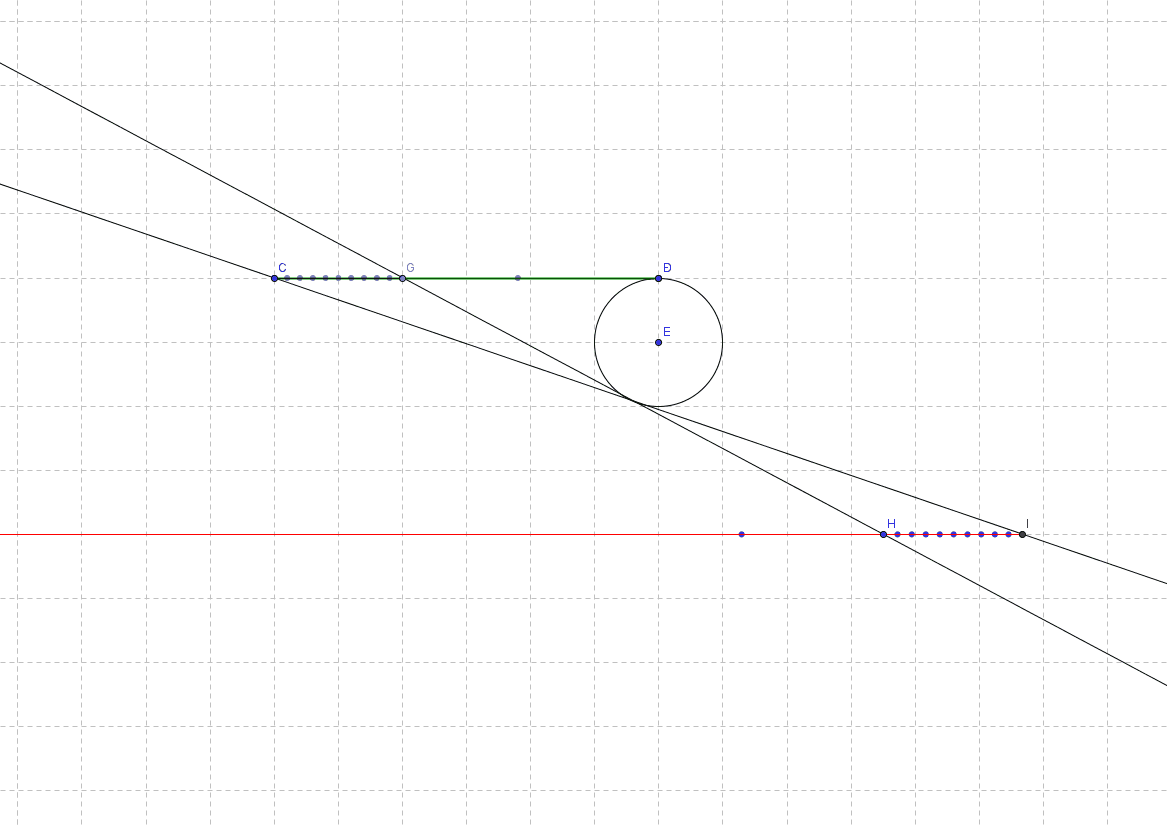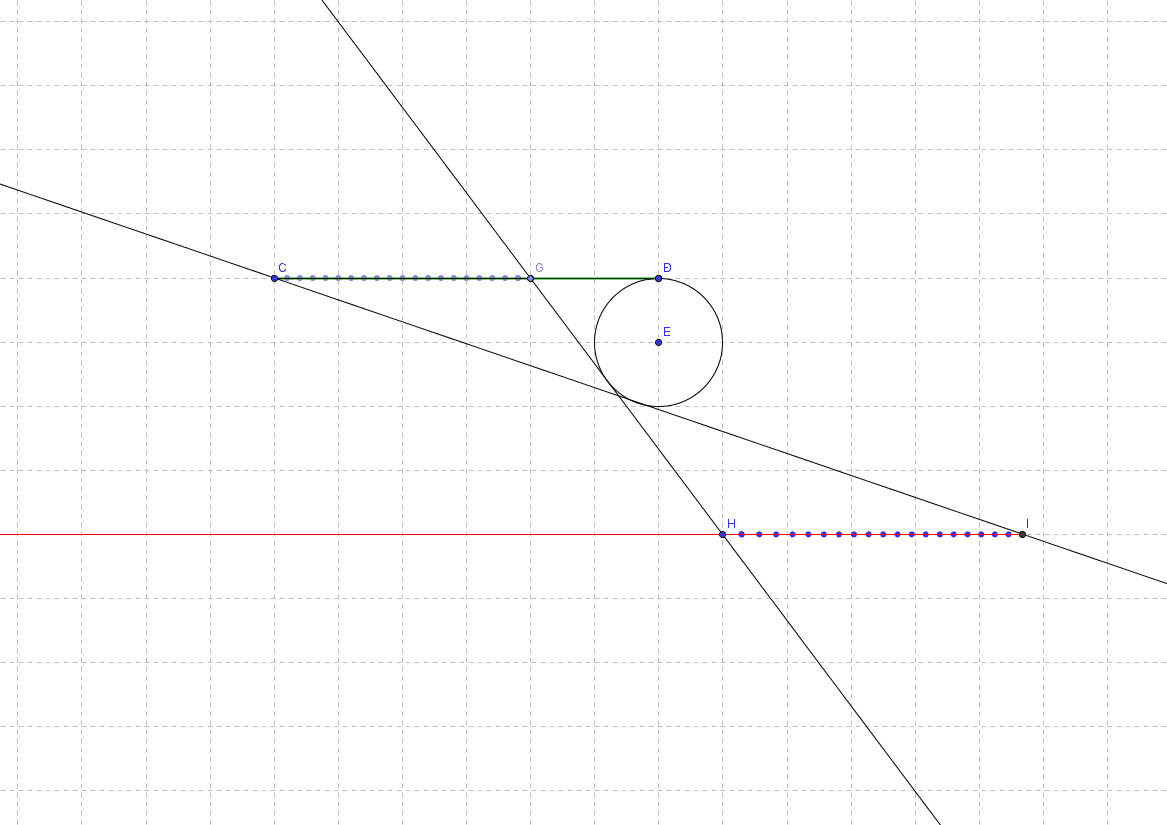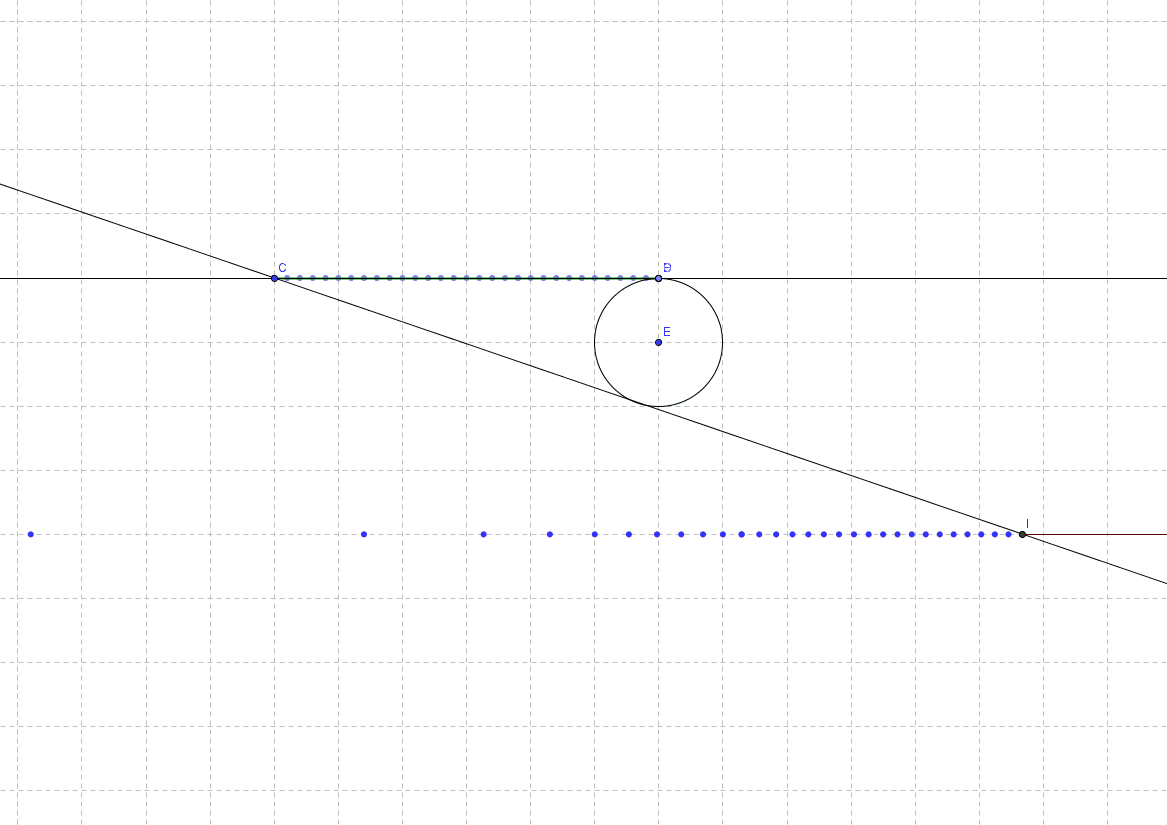
Well, geometrically, one can show very nicely continuous 1-to-1 correspondences (continuous in almost every point). E.g. a visual representation of why a segment has the same number of points as a ray (half a line if you prefer). 1. Take a segment [C,D) (That is with C but without D) 2. Consider a circle tangent to CD that contains D. 3. Construct a parallel line to CD over the other side of the circle 4. Let G be a moving point on the green segment CD. 5. Construct another tangent to the circle from G (as one tangent always follows line CD). 6. Denote H the point of intersection between this tangent and the parallel line. As G moves inside the green segment [C,D), H describes a red "ray" (-inf, I]. This 1-to-1 correspondence is seen in the following animation: Cannot find a simple geometrical way to get from 1-D space to 2D space (that would replace the interleaving proof in my previous post). A 1-to-1 correspondence between 2-dimensional space and 1-dimensional space has to "distort" that space a lot ... spreading two near points in a plan in very distant places on the line. So it's very hard to show it in a geometrical way. I know of infinite curves that can fill an unit square, but there not so easy to explain in an animation using GeoGebra. bonanova, is this (curves filling nD objects) what you were thinking about? I'm slowly running out of uploading space, so I'll probably need to delete some previously added images/posts.
-
Sneakin' a few more before anyone can stop me: NEWYORK XAPTKOFX WYOMING NJNIYAPN MICHIGAN HIHAPOJE 27 down, 24 to go Taking a break for a while since we've passed the midpoint.
-
And since I started ranting, let me continue with
-
Actually, after thinking a little more ... I almost had a proof but it had a hidden fallacy in it. Just putting it here maybe it inspires an actual proof. OFF-TOPIC I admit I still enjoy this puzzle as I'm a twisted-version of a researcher I enjoy mostly proving that something is either not possible or undecidable
-
Allowing for non-answers (head exploding) Seriously now Still not sure we need to delete this as we do not have a formal proof that it's impossible. I propose we leave it as an open question for now or as "Bushindo's 3-Randoms-Hiding-Successfully Conjecture"
-
Maine coming up ... MAINE NFOAJNFO LOUSIANA WKTJBPCM MARYLAND ASZMBPFM 24 down, 27 to go
-
Yes, your formula is indeed correct. Just compiled them both in a spreadsheet. They give the same results for all commands including ABORT. Surprisingly, the methods may yield different results for 2 and 3 letter words, but are equal for longer-than-5 letter-words and 4 letter-words, except those with 4 distinct vowels. It seems that my WeirdMod function + alpha + constant difference in definition of x (mine's is 0..1, yours is 1..2) just gives in a more complicated way the same array you do naturally with "position of the letter in command". E.g. for IOWA 41234123 is obtained by 2 variables and one function in my case. Not sure how exactly your digit adding function (if >10) is simulated with my variables, but it seems to work. That's why it always seemed unnatural to me. I went on on a wrong path and constructed artificial variables just to fit the data and bring me back to it. Guess this is kind of a physicist nightmare Thank you again for the challenge ... twice I really enjoyed first discovering my alternate-oh-so-complicated-but-still-fits-the-data-so-it-must-be-true-right theory and then your simple-oh-so-simple-how-did-i-miss-that-wait-they-both-cannot-get-the-same-results-can-they-oh-my-god-they-can-how-the-hell-is-that-possible theory.
-
VERMONT NPNUXGRN VIRGINIA JTHJNIBV NEWJERSEY LGRTGAPF 21 down, 30 to go.
-
-
Cord sever listed galaxy praise Adding with pressure
-
Queen indeed Q U E E N PLEAT - 1 STARE - 0 PLANE - 0 START - 0 SLEET - 2 GREEN - 3 QUEEN - 5 maquis +30 araver +6 Glycereine - 674 plainglazed - 580 Cherry Lane - 532 Izzy - 386 Vineetrika - 384 maurice - 312 Unreality - 284 dawh - 194 t8t8t8 - 190 NickFleming- 180 Framm - 177 golfjunkie - 170 woon - 141 araver - 129 Maquis - 126 Fabpig - 111 JarZe - 96 Blablah99 - 89 Harvey45 - 77 MollyMae - 46 Hirkala - 36 yuiop - 21 Abhisk - 20 PVRoot - 20 Filly - 19 Prince Marth - 15 DudleyDude - 15 phaze - 15 Kac_cotu - 5 You're up
-
I call and raise you INDIANA OHIO QQHIQQHI IDAHO JOKEAJOK INDIANA FJBPCJNF 18 down, 33 to go.
-
Not really. There are as may points in a unit square as in a segment. Similarly a plane has as many points as a plane. I know it sounds counter-intuitive but it's really not that absurd. I can convince you with the interleaving digits argument which basically is an extension of the odd/even argument. I am assuming that you believe that there is a correspondence between even numbers and odd numbers (f(x)=x+1 for every even integer x). Now if you shuffle back the evens and the odds putting one even then one odd, and so forth, you get all integers again. Long story short: For every real number x between 0 and 1 (your 1cm line) you can write an infinite sequence of decimal digits: x=0.x1x2x3 ... This can be written as an infinite sum: x = sumi>0 (xi /10i). The same applies for every real number, adding it's integer part to the left of the decimal point. The problem is that this digit decomposition is not unique as seen for 1 for example: 1=0.99999999999999999999999999... =1.00000000000000000000000000.... (there are several proofs for this result, not directly relevant to this discussion) However, this non-uniqueness only occurs when you get an infinite sequence of 0's. This is the case only for rational numbers, more precisely for rational x = p/q where q is of the form 2n5m, where n and m are positive integers (m,n>=0). So, you may get an unique decimal representation by simply banning an infinite sequence of 9's and choosing the other possible representation, ok? Back to the square. For every a and b real numbers you have two such unique-sequences as seen above (not ending in infinite 9's): a=0.a1a2a3 ... b=0.b1b2b3 ... By interleaving the two sequences you create an infinite decimal representation and therefore a real number x: x=0. a1b1a2b2a3b3 ... The beauty lies in the fact that for every point in that unit square, you get exactly one point on the unit segment (your 1cm line) and conversely each point on that unit segment can be split into (a,b) giving a point in the unit square. Convinced? Yes, I'll think of a nice (=geometric) 1-to-1 correspondence and post it. Simplest way I know has multiple steps square-rectangle-ray and so forth. P.S. I don't really like the interleaving digits or Cantor-Bernstein-Schroeder proofs either, but accept them
