sorry it is not y - A^n y

In binary modular arithmetic, y XOR Aⁿ y is indeed equivalent to (y - Aⁿ y), as the following table will show

Notice that for a and b in the discrete set (0, 1), (a XOR b) is indeed equal to (a + b) mod 2.

Every school boy or girl knows that with best play tic tac toe is a drawn game.

That is, getting three markers X or O in a row playing alternately on a 3x3 grid is impossible if your opponent plays correctly.

But suppose we extend the board to the plane - there is an unlimited number of squares on which to play.

Certainly then the first player can always achieve a row of 3 markers no matter how her opponent plays.

What is the largest number of markers in a row that first player can achieve in this case?

Here's an upper bound on the largest row length for which the first player can win

Here's a strategy which allows the second player to always draw if 9-consecutive markers are required to win,

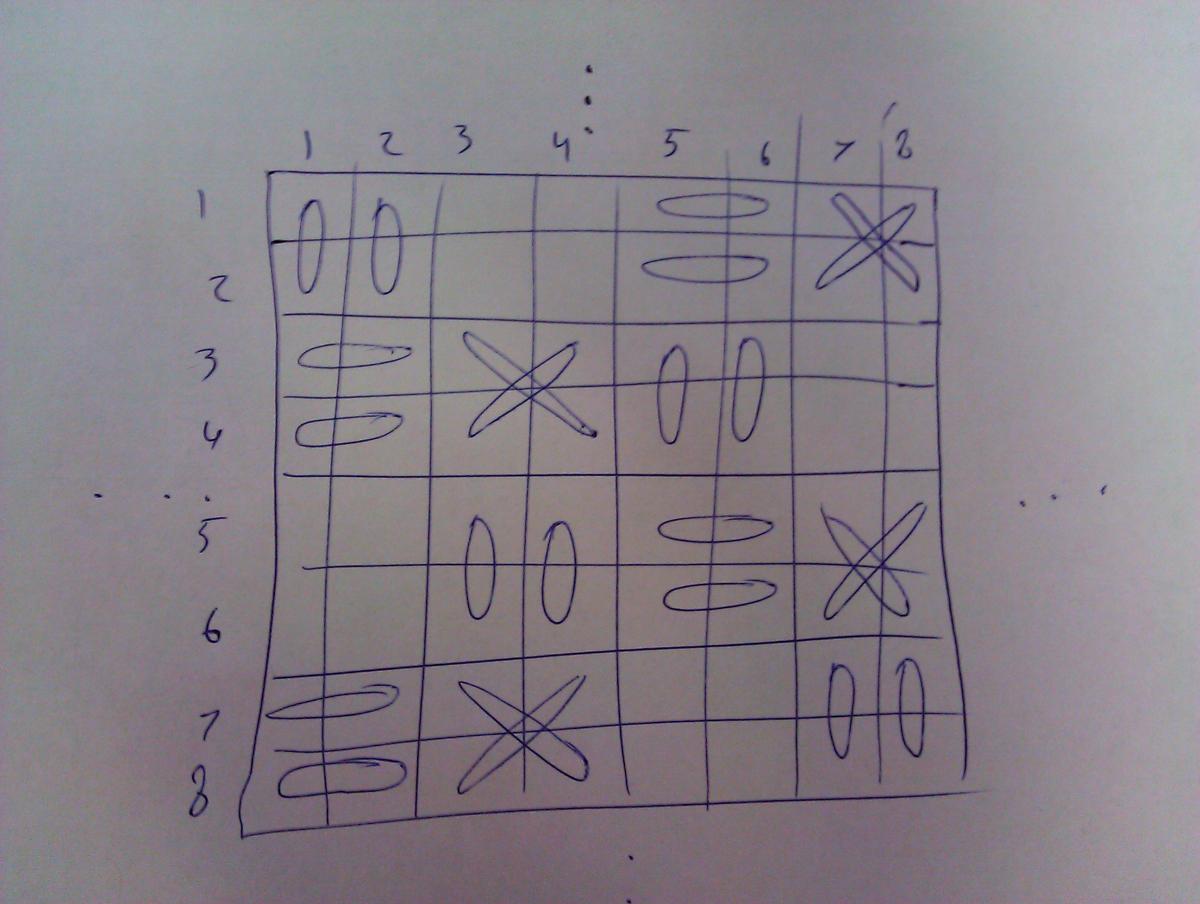
Divide the infinite plane into identical 8x8 sections. Within each section, pair certain squares up with certain other squares. When player 1 plays a marker within a matched square, play the corresponding square. The map of the pairs (shown by the badly drawn ovals) are as follows

For instance, if player 1 plays a marker at row 1, column 1, which we denote as (1,1), then player 2 should play a marker at square (2,1). Likewise, if player 1 plays a square at (3,3), player 2 should play at (4,4).

There are four 2x2 squares that are left empty with no pairings within them. Those 2x2 squares are not important to the strategy. If player 1 plays any square within any of the 2x2 squares, simply choose another box within the same 2x2 square and play that. For instance, if player 1 plays in square (1,3), we can choose to play (1,4), (2,3), or (2,4).

The true limit on the largest row length is probably smaller than 9, however.

great puppze.

very good puzzle.

if the initial is y, after shift it is A^n y, and after light up

it become y XOR A^n y

it is no y - A^n y.

I'm afraid I don't follow this post. With the last sentence, did you mean to say,

it is now y - A^n y,

or

it is not y - A^n y ?

Adding more hints for completing the proof. See post above for background.

The product of the operator (I - Aⁿ) is communicative. That is, (I - Aⁿ) (I - A^m) = (I - A^m) (I - Aⁿ).

Because A rotates the vector y by 1 space, then after 64 rotations, we are back to the original y. So,

I = A⁶⁴,

I - A⁶⁴ = 0,

5 sequences:

{10⁶/5^m-(5^m-1)/2,...,10⁶/5^m+(5^m-1)/2} for m=0,1,2,3,4.

So the 0th is just {1000000}, the 1st is {19998,...,20002},... and lastly the 4th is {1288,...,1912}. Namely, the 0th has just 1 "consecutive" term, the 1st has 5 consecutive terms,... and the 4th has 5^4=625 consecutive terms.

Had the question not said positive terms, there would be two more sequences when m=5 and when m=6.

There's another

that starts at 7749 and goes on for 128 terms.

Find a simple closed form expression for

the alternating series of squares,

n²-(n-1)²+(n-2)²-(n-3)²+...+4²-3²+2²-1².

It should be equal to

n²/2 + n/2

Adding additional hints for proving that the optimal strategy described by araver and superprimastic will guarantee a win

Let y be a binary 64-dimensional vector where 1's correspond to a lamp being on, and 0's correspond to a lamp being off. Let I be a 64x64 identity matrix, and let A be a rotation matrix that rotates the entire vector by 1 space. We can construct A by starting with an identity matrix and then 'lifting' the diagonal up 1 row. For instance, a small example of A that is 8x8 would be the following matrix

	[,1]	[,2]	[,3]	[,4]	[,5]	[,6]    [,7]    [,8]

[1,]	0	1	0	0	0	0	0	0

[2,]	0	0	1	0	0	0	0	0

[3,]	0	0	0	1	0	0	0	0

[4,]	0	0	0	0	1	0	0	0

[5,]	0	0	0	0	0	1	0	0

[6,]	0	0	0	0	0	0	1	0

[7,]	0	0	0	0	0	0	0	1

[8,]	1	0	0	0	0	0	0	0

So, if we are given a vector (a, b, c, d, e, f, g, h), then

A * (a, b, c, d, e, f, g, h)' = (b, c, d, e, f, g, h, a)'

A² * (a, b, c, d, e, f, g, h)' = (c, d, e, f, g, h, a, b)'

So, let's go back to the case where y is a 64-dimensional vector. We define A as a 64x64 rotation matrix. It is easy to see that a turn of the game where we apply the strategy described by araver and superprimastic correspond to the matrix

(I - Aⁿ)

where n is the number of spaces that the butler choose to turn the table clockwise before applying the switches. So, for instance, if we play 3 turns using the winning strategy, and the butler turned the table 5, 19, and 3 spaces, respectively, then the current state, y_c, corresponds to the followings

y_c = (I - A³) (I - A¹⁹) (I - A⁵) y

where all the calculations are done modulo 2.

but definately still a guess without proof. take the xor of the current position of lamps on (1s) and lamps off (0s) and 1010101...0 and that is the direction you give the butler. repeat until you get all lamps around the table on or off. if all end up off, make one last selection of switching all the lights.

Using the proof technique that I posted in post #8, I was able to verify that this strategy would also guarantee that we would win in the end. Good work!

Araver and superprimastic got the correct strategy ( nice analysis and intuition, araver). I'm interested in seeing more of superprimastic's input after the hurricane (be safe). As for me, I was able to prove that the strategy is guaranteed to win using

we let the list of lamps states be a 64-dimensional binary vector. There exist a matrix operator that corresponds to the strategy described by araver and superprimastic. Turns out that this operator has certain special properties, and applying it after a certain number of time will take the original vector to 0.

For clarification, the Butler may turn the table in any direction and as may spaces as he wants, right?

That is correct. The Butler may turn the table in any direction and for as many spaces as he wants.

Let's say that you are setting the dining table for a party of 64 guests. The 64 guests will be seated at a giant circular table. Each seat has a lamp, and currently some of the 64 lamps are on and some are off. The butler offers to play a game with you. Let's say that the chairs are labelled with the guests names, which for convenience we label starting from the top and going clockwise as G1, G2, ..., G64, and the chairs are stationary. The giant circular dining table along with the lamps, however, can rotate. Each lamp has a switch, and flipping the switch when the lamp is on turns it off, and vice versa. The game is as follows

1) The game consist of turns. At each turn, you tell the butler a list of chairs at which you want to switch the lamps' state.

2) The butler will then has the option of arbitrarily rotating the entire table before he apply the switches at the list of chairs in point 1). Please note that the butler must rotate the table in such a way that each chair is directly across from a lamp (rotating so that a lamp ends up midway between two chairs isn't allowed).

3) You may take as many turns as you'd like. If you succeed in turning all the lights on, you win.

Example: Let's say that currently all lamps are off except for the ones at G1, G3, and G5. You tell the butler to switch the lamps at G1, G3, and G5. The butler then rotates the table counter-clockwise 2 spaces. Now, the lamps at seats G63, G1, and G3 are on. The butler then proceed to switch the lamps at G1, G3, and G5. The end result is that now the lamps at G63 and G5 are on.

Show that there's a strategy that is guaranteed to turn all the lamps on.

... and reconsidering my n=3 case above, but with a different function than the one I posted before ( as f(x,x)=x f(x,y)=z is hard to generalize .. guess it was a remnant from one of my Mistery Ops), I believe there was a very quick general function all along.

Assume white=0, black =1, red = 2 (or something of the sorts, what's important is that all agree beforehand on the same conversion table):

f_n(x₁,x₂, ... x_n-1) = [2 - (x₁+x₂ + ... x_n-1) ] mod 3

or in other words (the above was just more of a quick feel of the new editor):

Add all the other hat numbers and guess the complement modulo 3.

Using the above function one guesses correctly his own hat color only if and only if the sum of all hats equals 2 modulo 3.

But when that happens, all of them guess correctly simultaneously (which I guess is easier to see with this function than it would for any other separation code I can think of).

Given the 3^n possible cases (uniform distribution), it is fairly easy to see that there are 1/3 chances of the sum of all hats to equal 2 modulo 3, leading to the (maximum?) 2/3 chances of all being incorrect at the same time ("synchronized out of phase" ).

Was this what you had in mind?

Yup, perfect solution. It's nice to see you around this New Puzzles forum once more. Reminds me of the grand old time when we solved 'Team of 15' together. Good old times =)

...nothing. If Prisoner A could, in some way, communicate the parity of a single hat colour a, we could get a guaranteed 27 incorrect guesses and a 2/3 chance at Prisoner A also getting his incorrect--everyone would know that his hat is either of colour a or not of colour a.

Hmm, very very interesting one.

My first thought is that the underlying idea may be to use a guessing function that acts like a "hard" separator (as in some other puzzles of the "same" type) : when at least X are correct, then all are correct, leaving a lot of cases or all (or most of all) are incorrect. By grouping together the correct guesses in the same scenario, intuitively, one maximizes the likelihood of all guessing incorrectly.

A couple of runs on smaller versions would probably make the above point clearer:

1) For 2 players, one can guarantee 2/3 chance of all guessing incorrectly with f₂(X)=X or informally each guesses the other's color. Out of 9 cases, in 6 of them none is correct and in 3 of them (RR, BB, WW) both are correct.

2) For 3 players, one can guarantee 2/3 chance of all guessing incorrectly with a similar function f₃(X,X)=X, f₃(X,Y)=Z.

This would get 3 correct guesses in all 3-0-0 situations and 2-1-0 situations and 0 correct guesses in the rest of the cases. 2/3 chance of getting "all wrong".

Now this "one fails, then all fail" intuitive grouping looks more likely to be optimal in problems where a win is defined as all guess incorrectly. If one could push it above n=3. That means finding a (rare) code over F₃ⁿ and instructing each of the players to compute their hat color as the "nearest" codeword given the other n-1 hats they can see.

But this particular problems asks for a finer point. Not getting "all wrong", but getting "all but 4 wrong".

Denoting N= no. of players and M = no. of maximum correct guesses, the (general) problem has a natural size attached to it - (M, N). So, the above approach may look fine for (2, 0) and (3, 0), but there seems to be a qualitative leap to reaching (28,4).

Setting optimal aside, a luckier than random shot could be constructed using smaller instances (though composition of smaller instances intuitively destroys optimality in this case). But all of the composition/decomposition-based variants I've toyed with so far led me to nothing in particular. So far. Which is why this post only contains this very rough idea. I actually hoped for a (7,1) solution. Assuming the chance of winning for (7,1) would be alpha, then by composing 4 such instances for the (28,4) problem, one would get a (suboptimal) alpha⁴ There may still be a cleverer way of composing the smaller instances, but I kinda doubt it at this point.

So, I'm back to leaping towards the (28,4) ternary function/code without a clue on how to actually construct it.

Not sure if the above is helpful in any way, :shrug:. Will check back when I get a working (28,4) "code"/function.

//

I'm going to come out and admit that the phrase '4 or less correct' is a red herring =). I have a winning rate of 2/3, and I believe avaver and molly are on a cusp of getting that solution.

Have everyone guess that there Hat color is BLUE.

Zero answers should be correct which is less than 4.

*Sign*, the brainden never ceases to amaze me with the out-of-the-box solution. Congratulations, you win the out-of-the-box solution. There's still the intended in-the-box solution where each person can only write down Red, Black, or White. No one has that solved yet.

^ You've got the upper bound right, but I think you could optimize it a bit more, here's the solution I thought of when I first started thinking of this riddle:

Let's say you have K pots with 2*K liters of water in them, you can sort them from fullest to least full and then take the first (fullest) pot and pour all but 2 liters into the second, take the second and pour all but 2 into the third and so on and so on, this would distribute the water in exactly K-1 steps, let's call this the trivial algorithm.

To improve on the trivial algorithm we can divide the pots into groups if there were 6 pots with 12 liters of water and we managed to divide them into 2 groups of 3 pots with 6 liters in each, then if we solve each group separately using the trivial algorithm we can do it in 4 steps instead of 5, ..

The general idea is that the more groups you divide the pots into the more steps you save, you save exactly one step each time you divide a single group into 2 groups.

So the algorithm is as follows, for each number K, starting from 1, search for goups of K pots that have 2*K liters in them and solve them separately using the trivial algorithm, so first you search for single pots that have 2 liters and solve them in 0 steps, then pairs of pots that have 4 liters and solve them in 1 step, then groups of 3 and solve in 2 steps and so on and so on..

you do not need to search for groups larger than N/2, because for example if there were 20 pots, if you haven't found any groups of size 1-10 you surely won't find a group of size 11 because if that group had 22 liters of water then the other 9 pots have 18 liters of water and so they are a group of 9...

The upper bond for this algorithm is still N-1 steps, there is always a distribution that cannot be solved in less than that (you can put all the water into a single pot, or you can distribute the water so that each pot holds an amount that has a fraction value of 1/N, for example if there were 20 pots make sure each pot has .05 liters)

Since you are interested in the 'fastest' algorithm, an computational complexity analysis is in order

The efficiency of an algorithm is often measured by the number of operations it needs to make. I'll just handwave here some and say that operations are steps that the computer must take in order to carry out an algorithm. For instance, we can think of an if comparison as an operation. We can also think of an addition procedure as an operation as well. The idea is the less operations we need, the faster the algorithm is.

In the trivial algorithm you mentioned, we first need to sort an list of size n. Optimal sorting is known to have on average (n log n ) operations. That is not bad, but there are ways to construct a trivial algorithm with linear complexity of (n).

The optimization you mentioned where you search for all subgroups of size k = (1, 2, ..., n/2) such that their total water is 2*k is probably more trouble than it is worth. There are a total of (_nC₁ + _nC₂ + ... + _nC_n/2 = 2^n-1) comparisons that you need to check. So let's say that n = 21. If we do a search for all possible subgroups, we will waste about 1,000,000 comparisons just to find what the subgroups are. On the other hand, if we apply the trivial algorithm without the subgroup search, we would be done in less than 30 operations.

You have n pots, each having a random amount of water in it, the total amount of water in all the pots is 2*n, you need to distribute the water among the pots equally so that each pot will have exactly 2 liters in it...

Find an algorithm to come up with the best solution with the minimum amount of steps, in each step you can only pour water from 1 pot to another...

Doesn't matter the complexity of the algorithm itself, only that the solution is shortest, but ofcourse faster algorithms are better...

How about this strategy

1) Sort the n pots into two sets A and B, where A consist of all pots with more than 2 liters, and B consist of all pots with less than 2 liters.

2) At every turn, pick a pot from A and a pot from B. There is a way to pour the water so that you'd get 1 pot with exactly 2 liters, and the other pot will belong to either A and B. (For instance, if pot a has 2.5 liters, and pot b has 1.7 liters, then pour .3 liters from a to b, and we end up with pots of 2 liters and 2.2 liters, respectively). Put the pot with exactly 2 liters aside, and put the other pot back into either A or B depending on its content. If we are lucky, then we might get two pots that are exactly 2 liters each, but that situation is trivial to deal with.

3) Repeat 2) for (n-1) times. Each time we remove 1 pot from A or B. After a maximum of (n-1) turns, we should be done.

This is confusing me now :L does it mean that if 1 or 2 or 3 or 4 people only, get their hat colour correct then they can leave? Meaning that if more than 4 people get their hat colour correct then they'd go back on the death row?

It is indeed as you say. If 0, 1, 2, 3, or 4 people got their color correctly, then everybody wins. Any more than that and they all go back to the death row.

They should all guess the same color agreed upon the night before. I (likely)

may have done the math wrong but I think it is a 99.99% chance that you have at

least 4 of 27 with that color.

Actually, you are right about the winning chance. I made a mistake in phrasing this puzzle. The condition should have been 'If 4 or less people got their hat color correct, then everybody wins.' In the incorrectly quoted version, the ideal solution is pretty much as you say. I fixed the wording the the original post.

<p>

</p>

<p>

They should all guess the same color agreed upon the night before. I (likely)</p>

<p>may have done the math wrong but I think it is a 99.99% chance that you have at</p>

<p>least 4 of 27 with that color.

</p>

<p>

</p>

<p> </p>

<p>Actually, you are right about the winning chance. I made a mistake in phrasing this puzzle. The condition should have been 'If 4 or less people got their hat color correct, then everybody wins.' In the incorrectly quoted version, the ideal solution is pretty much as you say. I fixed the wording the the original post.</p>

This is a classic puzzle. I first saw it about 1960. Do not consider physical restraints, your friend has a container of an infinite number of balls, each numbered sequentially. At 11:00 AM, he places balls 1-10 into your box and you throw out ball number 1. At 11:30 AM process is repeated for balls 11-20 and you throw out ball number 2. This continues by halving the time until noon each time and placing the next sequence of balls in your box and you throwing out the next in the sequence. Question: at noon, how many balls are in the box?

Here is an interesting twist to this puzzle

Suppose that we have an infinite number of balls, and we label them with odd numbers 1, 3, 5, 7, 9, 11, and so on.

1) On turn i, for i = 1, 2, 3, ..., we put 10 balls with the smallest indexes into the box. So, for turn 1, we put in balls (1,3, 5, ..., 19); for turn 2, we put in balls (21, 23, ..., 39 ), and so on.

2) On turn i, after we are done with step 1), we 'remove' the ball with the index i from the box by relabeling it as ball 2*i. So, for turn 1, we put in balls (1,3, 5, ..., 19), and then we relabel ball 1 as ball 2. For turn 2, we relabel ball 2 as ball 4, and so on. Notice that we are not physically taking any ball from the box at all; we are simply relabeling balls i as ball 2*i during every turn.

Now, since we can argue that for any ball index i, we can calculate the time after which there is no such indexed ball in the box, then the box must be empty when the process is finished. For instance, after turn 179, there is no ball in the box that is numbered 179.

However, another argument is that since we never physically remove any ball from the box, the box must be infinitely full.

Let's say that you and 27 other prisoners are on a death row. The warden gives you and your fellow prisoners a chance to win your freedom through a game. The game is as follows,

1) When the game starts, the warden will blindfold all 28 prisoners and arrange them in a circle.

2) The warden will put on each prisoner's head either a RED, BLACK, or WHITE hat. The warden will choose the color for each prisoner uniformly by tossing a fair die.

3) The warden will then remove the blindfolds. Every prisoner will be able to see the hats on the other 27. Each person will not know the color of his own hat.

4) The warden then gives everybody 1 minute so that each person can think about what his hat color is. At the end of that 1 minute, the warden will provide each prisoner with some paper, and all 28 prisoners must write their hat color at the same time. If 4 or less people got their hat colors correct, then everybody win their freedom. Otherwise, they all go back on the death row.

5) Each person is absolutely not allowed to communicate with his fellow prisoners during the game by speaking, facial expressions, body language, etc. The warden reserves the right to cancel the game and put everybody back on the death row if he see these types of behavior.

You and your 27 friends have 1 night to discuss a strategy. Find a strategy that makes your chances of freedom as high as possible.

EDIT: fixed a wording mistake that was pointed out by smoth333

Congratulations to CaptainEd and witzar for the nice solve. I'm glad you enjoyed the puzzle. I'm working on another one and will post it soon.

Select one prisoner to begin. Have the prisoner 10 from him clockwise stare at the clock if his hat is red, and at the table if his hat is black. The prisoner that begins then raises his hand and states his hat color. Each prisoner in clockwise area repeats the process, until all prisoners are done.

I think this would violate provision 5) in the OP, which states that each person is not allowed to communicate to his fellow prisoners during the game by varying his tone of voice, volume, facial expressions, body language, etc. Also, please consider using spoiler for your answers since other people may want to work on the solution on their own.

Use the Team of 15 approach as before. Player A announces his/her hat color at 1 minute if parity over the team of 20 is even and 1:30 if odd. Then everybody can compute their own color and announce any time they want.

This is a huge improvement over the previous bar set by Molly. It is still sub-optimal, although you're approaching the ceiling

The use of the solution for 'Team of 15' is very creative. I did not think of that possibility at all. The chance of announcer A successfully guessing his hat color and thereby winning the game is 15/16, or about 93.75%.

It is possible to get a winning rate that is over 99%, however.

Someone proposes something like this in every hat puzzle and every time it is against the rules. And then someone comes on and says "Imagine instead that they are isolated in a room..."

I think the biggest hole here is that when you raise your hand you must shout the colour of your hat.

The best I can come up with is actually the parity answer where one person takes a 50/50 and the circle continues.

I came up with this as I was thinking about it.

Or appoint two people--a primary and a secondary. The primary is going to make a guess when precisely 5 minutes has elapsed, unless the secondary is wearing a red hat. After the 5 minutes has elapsed and the primary hasn't guessed, he will raise his hand and shout red at the end of another 5 minutes (the number of minutes is arbitrary) unless shouting red throws off the parity (say the parity is defaulted to 0--he sees an even number of red hats). If, at the end of 10 minutes, the secondary has not shouted, the primary will shout red if he sees an odd number of red hats (he now knows the parity).

*note: this is very poorly worded, but it works. After those two have established the parity, everyone will know the colour of his own hat..

Your strategy is not optimal yet. It is a good beginning step, though

So, your strategy requires the primary person to raise his hand and guess at 5 minutes into the game if the secondary person has a BLACK hat (1 in 2 chance). So, suppose that the secondary person does have a BLACK hat, then the primary person have a 1/2 chance of guessing correctly. That means your strategy would result in 1- (1/2)*(1/2) = 3/4 winning rate.

This is a good start. However, the optimal winning rate is much higher than 3/4.

agree to raise your left arm if the prisoner across from you is red, and the right arm if black.

You found a loophole that I didn't think about when I tried to box the out-of-the-box solutions. Having a choice of which arm to raise is not intended in the OP, however, I don't see how it can help improve the winning rate beyond strategies like Molly Mae's. Can you flesh out your strategy so that we can compute a winning rate?

If the Clocks have a reflective surface (Like when you look at yourself in a car window etc.) could all the prisoners look at the clocks, see his reflection and then be able to say the colour of his hat correctly???

It's just a thought...

Let's say that the clocks have non-reflective surfaces. Nice out of the box thinking, though.

The prisoners are stood in a circle and there is an even amount (20 prisoners)

They are allowed to raise their hands right? so if they plan to wor with the man directly opposite him (as in being able to co-operate and work with all the men so that once in the circle they could work with the man directly opposite him), they could come up with a plan like this....

If the man opposite him has a red hat they will raise their hand after exactly 5 minutes and if he has a black hat on, he will not raise hi hand. they will then know what colour hat they are wearing and can say it to gain freedom.....

The raising of the hands would have to be done at the exact same time as the men will be blindfolded and therefore wouldn't be able to guarantee which man he would be helping

Also.... only after all those with red hats have spoken their colour would those with black hats be able to speak

Hope this Helps and I think this would work? (Well I hope it would anyway)

This is also interesting out of the box thinking. However, let's assume that each prisoner is required to shout his hat color at the same instant that he raises his hand.