-
Posts
719 -
Joined
-
Last visited
-
Days Won
5
Content Type
Profiles
Forums
Events
Gallery
Blogs
Posts posted by bushindo
-
-
Two correct answers! witzar and max0r4axor came to the right conclusion.
I think this paradox is a lot deeper than it seems. The mathematical community, at least, doesn't seem to agree on a single answer to this problem.
This is known as the ross-littlewood paradox. The categories of answers run the gamut from 'the box is infinitely full', to 'box is empty', to 'Problem is underspecified', to 'Problem is ill-formed'. For instance, here's an article by mathematician John Byl published in 2000 that states that the box is full (http://www.csc.twu.ca/byl/little.fin.doc )
-
1 more time
Cards to discard
1: 7♥ 8♣ 2: K♠ 3: 9♣ 4♠ J♣ 4: 6♥ 4♦ 5: Q♠ 8♣ 6♦ 7♠ 6: 5♦ 7♦ 7: 7♥ 2♠ 5♠ J♣ 8: J♦ 8♣ 9♠ 9: 3♦ 6♠ 4♠ 10: 7♠ Q♥ 11: 7♣ 12: NONE 13: 3♠ 14: 2♠ 15: J♠ 2♥ 8♦ Q♠ 16: NONE 17: 5♠ 18: 2♦ 8♥ 5♥ 9♣ 6♦ 19: 8♠ Q♦ K♠ 6♠ 20: 3♣ 4♦ J♥ 2♣ 10♥
-
This seems fun.
Cards to discard
1: 7♥ 8♣ 2: 8♣ 9♣ 10♠ J♠ 3: 9♣ 4♠ 4: 6♥ 4♦ 5: Q♠ 8♣ 6♦ 7♠ 6: 5♦ 7♦ 7: 7♥ 2♠ 5♠ J♣ 8: 8♣ 9♠ 9: 3♦ 6♠ 4♠ 10: 7♠ Q♥ 11: 4♠ 5♠ 6♠ 12: NONE 13: 2♣ 4♣ 5♣ 14: 3♣ 4♣ 5♣ 15: J♠ 2♥ 8♦ Q♠ 16: NONE 17: 3♦ 4♦ 6♦ 5♠ 18: 2♦ 8♥ 5♥ 9♣ 6♦ 19: 8♠ Q♦ K♠ 6♠ 20: 3♣ 4♦ J♥ 2♣ 10♥
-
Listed below are 20 poker hands.
For each of the hands below, assume
it was dealt to you from a full shuffled
poker deck of 52 cards. You may stay
with the hand you are given or discard
any number of its cards. Any discarded
cards will be replaced by a random draw
from the remaining 47 cards. Your goal
is to improve the value of your hand as
much as possible. List which cards, if
any, you should discard from each of the
starting hands below:
1: 10♦ A♠ 10♥ 7♥ 8♣ 2: K♠ 8♣ 9♣ 10♠ J♠ 3: 9♣ 8♦ 8♥ 4♠ J♣ 4: 6♥ K♦ A♦ K♥ 4♦ 5: Q♠ 8♣ A♥ 6♦ 7♠ 6: 3♣ K♠ 5♦ 7♦ 3♥ 7: K♠ 7♥ 2♠ 5♠ J♣ 8: J♦ 10♣ 10♥ 8♣ 9♠ 9: 3♦ 6♠ 5♠ 4♠ 5♦ 10: 5♠ 7♠ 5♦ A♠ Q♥ 11: 4♠ 5♠ 6♠ 7♠ 7♣ 12: 2♠ 3♣ 4♣ 5♣ 6♣ 13: 3♠ 2♣ 3♣ 4♣ 5♣ 14: 2♠ 2♣ 3♣ 4♣ 5♣ 15: J♠ K♠ 2♥ 8♦ Q♠ 16: 2♠ 3♠ 4♠ 5♠ 6♣ 17: 3♦ 4♦ 6♦ K♦ 5♠ 18: 2♦ 8♥ 5♥ 9♣ 6♦ 19: 8♠ Q♦ A♠ K♠ 6♠ 20: 3♣ 4♦ J♥ 2♣ 10♥
Usual poker hand rankings apply.
So, for example, "round the corner"
straights are not allowed, although
an ace may be either high or low card
in a straight.
Some clarification please. In the bolded passage, what do you mean by "improve the value of the hand as much as possible"?
Does it mean discard the hand so as to maximize the chance of drawing a better hand, and that all better hands count equally? E.g. if we have a pair, then an improvement to 2 pairs counts the same as an improvement to a royal flush?
Does it mean discard some cards so that we maximize the expected 'value' of the new hand for some payoff scale? If so, what is that payoff scale?
-
This thread took a few days to get going but eventually didn't disappoint. Nicely done plainglazed. About a week ago, I thought of this triple balance scale concept and how quickly you can glean a massive amount of info after a few weighings. 16 seemed like such a simple and efficient answer, but i'm not surprised that this forum blew that away. Glad I didn't spend a long time writing out my solution for 16 now. LOL
These kinds of problems are always tougher to write out than to think about.
How about 21?
Here's a case for 21.
Let's say that we label the marbles 1-21. In the first weighting (W1), assign each marble to a pan using the following scheme.
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13] [,14] [,15] [,16] [,17] [,18] [,19] [,20] [,21] W1 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 0 0 0 0 0 0where the row indices represent the marble number, and the number below each row index indicates the pan number (1,2, or 3) that it should go to. A 0 indicates that the corresponding marble will be unweighted. There are three categories of outcomes. The first is that all three pans will have the same height. The second outcome is that exactly two pans will have the same height, and the last outcome is that the three pans have 3 different heights. We only solve the most difficult case where the three pans have the same height (this is because this case has the most potential marble configurations). The other two cases can be solved straightforwardly. So, let's say that in the first weighing, the three pans have the same height. Assign the second weighing (W2) as follows[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13] [,14] [,15] [,16] [,17] [,18] [,19] [,20] [,21] W1 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 0 0 0 0 0 0 W2 1 2 3 0 1 2 3 0 1 2 3 0 1 2 3 0 1 2 3 0 0To understand what is going on, it may help to think that we have *four* pans, real pans number 1, 2, 3, and a virtual pan called 0 (this simply consists of all marbles that are unweighted). In the second weighing, we essentially take 3 marbles from each pan and distribute them to the other 3.
Again, we only examine the most difficult case, which is where the all three pans again have the same height. In this situation, we can see that there are 12 possibilities
(16+, 20-)
(16+, 21-)
(20+, 21-)
(16-, 20+)
(16-, 21+)
(20-, 21+)
(1+ , 5-)
(6+ , 10-)
(11+, 15-)
(1- , 5+)
(6- , 10+)
(11-, 15+)
where (11-, 15+), for instance, denotes that marble 11 is light, and marble 15 is heavy. Note that only 1 of these 12 possibilities is actually true, and the rest are all normal marbles. We can narrow these 12 possibilities down to 1 with the last weighing. So, for W3, put marble 16 and marble 1 on pan 1, put marble 20 and marble 6 on pan 2, and put marble 21 and marble 11 on pan 3.
If weighing 3 results in three different pan heights, then we know that the light/heavy pair must occur within the top 6 possibilities in the list above. If the weighing results in exactly 2 same heights, then we know that the light/heavy pair must occur within the bottom 6 possibilities. Depending on the exact pan-configurations, it is fairly easy single out exactly which pair it is.
In this outline we only looked at the most difficult class of outcomes, and showed that those are solvable. The remaining outcomes are not as hard, and we'll omit them here.
-
a case for 19? First compare 6 marbles on each pan. Let's call them a1,a2,a3,a4,a5,a6 vs b1,b2,b3,b4,b5,b6 vs c1,c2,c3,c4,c5,c6 One of three general outcomes can occur: I. If one pan is high or low and the other two equal: -lets say pan "a" was low meaning one of a1,a2,a3,a4,a5,a6 is heavy and the 19th marble must be light. compare a1 vs a2 vs a3 to see which one might be heavy then, if those are equal, compare a4 vs a5 vs a6 to find the heavy marble II. If one pan is low indicating a heavy marble and one pan is high indicating a light marble. -lets say pan "a" is low so one of a1,a2,a3,a4,a5,a6 is heavy and pan "b" is high so one of b1,b2,b3,b4,b5,b6 is light compare a1,a2,X vs a3,a4,X vs b1,b2,b3 where X is a previously established "normal" marble if all are equal, then a5 or a6 is heavy and either b4 or b5 or b6 is light so one of the following must be true: a5H,b4L a5H,b5L a5H,b6L a6H,b4L a6H,b5L a6H,b6L compare a5 vs b4 vs b5 if they are are equal then a6 is heavy and b6 is light if only a5 is heavy then b6 is light if only b4 is light then a6 is heavy if only b5 is light then a6 is heavy or a5 is heavy and b4 is light or a5 is heavy and b5 is light if a1,a2,X (or a3,a4,X) is heavy and b1,b2,b3 is light then one of the following heavy,light combinations must be true: a1H,b1L a1H,b2L a1H,b3L a2H,b1L a2H,b2L a2H,b3L compare a1 vs b1 vs b2 if they are are equal then a2 is heavy and b3 is light if only a1 is heavy then b3 is light if only b1 is light then a2 is heavy if only b2 is light then a2 is heavy or a1 is heavy and b1 is light or a1 is heavy and b2 is light if a1,a2,X (or a3,a4,X) is heavy and b1,b2,b3 is "normal" then either b4 or b5 or b6 is light so either: a1H,b4L a1H,b5L a1H,b6L a2H,b4L a2H,b5L a2H,b6L compare a1 vs b4 vs b5 similarly to above III. If all three pans are equal then BOTH the heavy and light marble are in one of a1,a2,a3,a4,a5,a6 or b1,b2,b3,b4,b5,b6 or c1,c2,c3,c4,c5,c6. compare a1,b1,c1,a4 vs a2,b2,c2,b4 vs a3,b3,c3,c4 if all are equal then the heavy and light marble are either a1,a4 b2,b4 c3,c4 a5,a6 b5,b6 c5,c6 compare a1,b2,c3 vs b4,a6,b6 vs c4,b5,c5 if only a1,b2,c3 is light then a1L,a4H if only a1,b2,c3 is heavy then a1H,a4L if only b4,a6,b6 is light then a6L,a5H if only b4,a6,b6 is heavy then a6H,a5L if only c4,b5,c5 is light then c5L,c6H if only c4,b5,c5 is heavy then c5H,c6L if a1,b2,c3 is heavy and b4,a6,b6 is light then b2H,b4L if a1,b2,c3 is light and b4,a6,b6 is heavy then b2L,b4H if b4,a6,b6 is heavy and c4,b5,c5 is light then b6H,b5L if b4,a6,b6 is light and c4,b5,c5 is heavy then b6L,b5H if c4,b5,c5 is heavy and a1,b2,c3 is light then c3L,c4H if c4,b5,c5 is light and a1,b2,c3 is heavy then c3H,c4L if say a1,b1,c1,a4 is heavy and a2,b2,c2,b4 is light then one of the following heavy,light combinations must be true: a1H,a2L a4H,a2L b1H,b2L b1H,b4L c1H,c2L compare a2,b1 vs a4,b4 vs c1,c2 if all are equal then c1H,c2L if only a2,b1 is light then a1H,a2L if only a2,b1 is heavy then b1H,b2L if a2,b1 is heavy and a4,b4 is light then b1H,b4L if a2,b1 is light and a4,b4 is heavy then a4H,a2L if only one pan is heavy or light, say a1,b1,c1,a4 is heavy then one of a5, a6, b5, b6, c5, c6 is light so the following combinations are possible: a1H,a5L a1H,a6L a4H,a5L a4H,a6L b1H,b5L b1H,b6L c1H,c5L c1H,c6L compare a1,c5 vs b1,a6 vs c1,b5 if all are equal then a4H,a5L if only a1,c5 is heavy then a1H,a5L if only b1,a6 is light then a4H,a6L if only b1,ah is heavy then b1H,b6L if only c1,b5 is heavy then c1H,c6L if a1,c5 is heavy and b1,a6 is light then a1H,a6L if b1,a6 is heavy and c1,b5 is light then b1H,b5L if c1,b5 is heavy and a1,c5 is light then c1H,c6L am skeptical that I have not screwed something up but have been looking at it too long to find out where.
The logic seems good to me. The first part of step III is particularly nice as it extracts maximum information out of the 3rd weighing. Great work, plainglazed!
-
I agree with this number. I'll let bishindo post his solution first. I'll post mine later if we don't hear form him today.
I now can do 1 better than that
I can do 17. Some preliminary details first. Let's label the marbles 1 to 17. For the first weighting, put marbles 1-4 onto pan number 1. Put marbles 5-8 onto pan number 2, and then put marbles 9-12 onto pan number 3. We can represent this weighing with the following notation
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13] [,14] [,15] [,16] [,17] W1 1 1 1 1 2 2 2 2 3 3 3 3 0 0 0 0 0where the row indeces represent the marble indeces, and the number beneath each row index represents which pan it goes in. We use 0 to indicate that a marble is not included in the weighing. The first weighing will result in 3 categories of outcome. The first is that all three pans will have the same height. The second outcome is that exactly two pans will weight the same, and the last outcome is that the three pans have 3 different heights. The first situation (the three pans all weight the same) is the most difficult, because it has the most potential marble configurations. We solve the first situation, and the remaining two will be trivial. So, suppose that the first weighting shows that all three pans have the same height. That means that the heavy and light marbles MUST occur together within marbles 1-4, or within marbles 5-8, or within marbles 9-12, or within marbles 13-17. We take advantage of that fact, and rearrange the marbles in the second weighing so that the heavy and light marbles are forced to be in different pans (unless the heavy and light marbles occur exactly at marbles 13 and 17). So, for the second weighing, assign the following marbles to the pans[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13] [,14] [,15] [,16] [,17] W1 1 1 1 1 2 2 2 2 3 3 3 3 0 0 0 0 0 W2 1 2 3 0 2 3 0 1 3 0 1 2 0 1 2 3 0Depending on the result of weighing 2, we can determine 4 or 5 possible heavy/light pairs, and then we can narrow it down with the last weighing.
For instance, let's say that the 3 pans all weight in same in weighing 2, that means that marble 13 and marble 17 is the heavy/light pair, and we can determine which is which with the last weighing.
For another example, suppose that the the second weighing gives for following heights for pans 1,2, and 3 - (a, a, b), where b < a. This means that for the second weighing, the light marble must occur in pan 3, and the heavy marble must be in the unweighted group. Looking the the table above, we can work out that the heavy/light marbles must be one of the following pairs.
(13+, 16-)
(17+, 16-)
(4+ , 3-)
(7+ , 6-)
(10+, 9-),
where (10+, 9-), for example, means that marble 10 is the heavy marble, and marble 9 is the light one. Remember only one of those 5 pairs are true, and the rest all weight 10 units. We can use that fact to narrow those 5 down with the 3rd weighing. So for the last weighing, put marble 13 and marble 3 on pan 1, put marbles 17 and marble 6 on pan 2, and then put marble 9 and marble 1 (which is now known to be a *good* marble) on pan 3. Depending on the light/heaviness of the pans, we can now tell which configuration it is.
-
Minor improvement
I can do 12. I think that is near the limit. I am working on possible improvement.
I think I can do 16. I'm about to board an airplane now, so I'll elaborate later.
-
Minor improvement
I can do 12. I think that is near the limit. I am working on possible improvement.
-
I don't think it's impossible.
I have a 4x4 Rubik's cube like the one in the OP, and awhile ago I looked up instructions on how to solve it. The cheats are not mine, but they do address the question. And there IS a set of moves to flip flop those two pieces.
All you have to do is turn the cube on its side, so the blue face is facing you, and the red face is facing up. In the attached image, straight arrows represent turning the designated horizontal layer (from the front perspective), and curved arrows represent turning the designated layer in depth.
If you want to test it out on a real cube, do the set of moves in the attachment, just omit the first 2 and do them at the end instead. This will get the cube to look like the OP. Then simply do the whole move, and the 2 wrongly-colored squares will change positions.
Mea culpa. The puzzle is flawed and wasn't completely thought through. I apologize. Congratulations to hettieann for the counter example.
I developed this puzzle along the lines of araver's previous post, namely that the rotations of the 4x4x4 cube will preserve the odd/even signature of the permutation, while a transposition will actually change the parity. Jumped the gun, I suppose =)
-
Everyone knows that the Rubk's Cube is unsolvable through pivoting or rotation of the cube planes. The only way to solve it is to remove and reapply the stickers, or modify an image in paint as you have done above.
The bolding in the quote is mine. I assume by Rubik's cube you mean the specially-modified cube in my OP. The question in the OP is not whether such a cube is solvable, but rather why is it not solvable. In other words, I'm asking for a proof that no sequence of rotations or pivots will return the cube to the traditional solved state.
-
Let's consider the following 4x4x4 Rubik's Cube,
The above cube is in the solved state (each of the 6 faces has identical color). I now take some paint and paint over two squares so that the resulting cube now looks the image below,
Notice that essentially we swapped the position of a red with that of a blue square. The top face and the three faces hidden from view are unchanged. Show that, using the normal pivoting and rotating operations of Rubik's cube, it is not possible to return the cube to the solved state like that of the first image.
-
Consider 25 colored envelopes. There are 10 envelopes of one color,
7 envelopes of a different color, 5 envelopes of yet another color,
and 3 envelopes of still another color. Each of the envelopes of the
rarest color (i.e., the color for which there are precisely 3 envelopes)
contain $100. The other envelopes contain nothing. You don't know
which number of envelopes is assigned to which of the four colors.
Now, these envelopes are randomly shuffled and shown to you one at
a time. As you are presented with an envelope you have two choices.
You may stop the game at that point, in which case you get to keep
the contents (if any) of that envelope. If you decide not to stop
the game at that point, the envelope is thrown away without being
opened and you are presented with the next envelope. You can only
see one envelope at a time, but you may record the colors of the
envelopes presented to you.
Find a strategy which will give you the best chance of getting $100
from playing this game.
I have done a simulation using the following strategy which gets
the $100 with probability about .49:
Keep a count of how many of each color you have seen so far,
including the one you are currently looking at. If the count of
the color you are currently seeing is less than or equal to the
counts for each of the other colors, take the envelope you are
looking at. Otherwise, continue the game.
I have found another strategy which wins with probability a bit bigger
than .75, according to my simulator. Can you find a better strategy?
Of course you'd get a bonus if you could compute the probability
of winning without resorting to computer simulation.
Here's the computation of the winning percentage. It isn't as elegant as I would like, so if there's a better way, I'd love to hear about it.
The strategy is to wait and only consider picking an envelope of any color on the third time that it shows up. In the entire game, that option will only present itself 4 times, 1 for each color. A little thought shows that it makes sense to pick the color that is the last to appear in 3 envelopes. Now, the computation of the winning chance.
Let's suppose that we label the colors A, B, C, and D, which have the frequency of 10, 7, 5, and 3, respectively. Let the state of the game at any point be (a, b, c, d), where a is the number of color A we have seen so far, b is the number of color B, etc. Given such a state vector, the chance that our strategy wins, P( a, b, c, 3), is
where a, b, c >= 3, and N = (a + b + c + 3). In order for our strategy to win, d must be equal to 3, and the N-th envelope to show up must be of color D. Now the task is to enumerate over 120 states where 3 <= a <= 10, 3 <= b <= 7, 3 <= c <= 5, and d = 3, and apply the previous equation to find the probability of winning. We then simply sum up all the probability. The total probability of winning is 0.7867886. I attach below the list of all 120 states and their respective winning probability.
Color A Color B Color C Color D N Probability 1 3 3 3 3 12 0.00202 2 3 3 4 3 13 0.00093 3 3 4 3 3 13 0.00186 4 4 3 3 3 13 0.00326 5 3 3 5 3 14 0.00020 6 3 4 4 3 14 0.00101 7 3 5 3 3 14 0.00121 8 4 3 4 3 14 0.00177 9 4 4 3 3 14 0.00353 10 5 3 3 3 14 0.00424 11 3 4 5 3 15 0.00026 12 3 5 4 3 15 0.00077 13 3 6 3 3 15 0.00051 14 4 3 5 3 15 0.00045 15 4 4 4 3 15 0.00225 16 4 5 3 3 15 0.00270 17 5 3 4 3 15 0.00270 18 5 4 3 3 15 0.00540 19 6 3 3 3 15 0.00450 20 3 5 5 3 16 0.00023 21 3 6 4 3 16 0.00039 22 3 7 3 3 16 0.00011 23 4 4 5 3 16 0.00067 24 4 5 4 3 16 0.00202 25 4 6 3 3 16 0.00135 26 5 3 5 3 16 0.00081 27 5 4 4 3 16 0.00405 28 5 5 3 3 16 0.00486 29 6 3 4 3 16 0.00337 30 6 4 3 3 16 0.00675 31 7 3 3 3 16 0.00385 32 3 6 5 3 17 0.00014 33 3 7 4 3 17 0.00010 34 4 5 5 3 17 0.00072 35 4 6 4 3 17 0.00120 36 4 7 3 3 17 0.00034 37 5 4 5 3 17 0.00144 38 5 5 4 3 17 0.00432 39 5 6 3 3 17 0.00288 40 6 3 5 3 17 0.00120 41 6 4 4 3 17 0.00600 42 6 5 3 3 17 0.00720 43 7 3 4 3 17 0.00343 44 7 4 3 3 17 0.00685 45 8 3 3 3 17 0.00257 46 3 7 5 3 18 0.00004 47 4 6 5 3 18 0.00051 48 4 7 4 3 18 0.00036 49 5 5 5 3 18 0.00183 50 5 6 4 3 18 0.00306 51 5 7 3 3 18 0.00087 52 6 4 5 3 18 0.00255 53 6 5 4 3 18 0.00765 54 6 6 3 3 18 0.00510 55 7 3 5 3 18 0.00146 56 7 4 4 3 18 0.00728 57 7 5 3 3 18 0.00874 58 8 3 4 3 18 0.00273 59 8 4 3 3 18 0.00546 60 9 3 3 3 18 0.00121 61 4 7 5 3 19 0.00019 62 5 6 5 3 19 0.00157 63 5 7 4 3 19 0.00112 64 6 5 5 3 19 0.00393 65 6 6 4 3 19 0.00655 66 6 7 3 3 19 0.00187 67 7 4 5 3 19 0.00374 68 7 5 4 3 19 0.01123 69 7 6 3 3 19 0.00749 70 8 3 5 3 19 0.00140 71 8 4 4 3 19 0.00702 72 8 5 3 3 19 0.00843 73 9 3 4 3 19 0.00156 74 9 4 3 3 19 0.00312 75 10 3 3 3 19 0.00031 76 5 7 5 3 20 0.00071 77 6 6 5 3 20 0.00415 78 6 7 4 3 20 0.00296 79 7 5 5 3 20 0.00711 80 7 6 4 3 20 0.01186 81 7 7 3 3 20 0.00339 82 8 4 5 3 20 0.00445 83 8 5 4 3 20 0.01334 84 8 6 3 3 20 0.00889 85 9 3 5 3 20 0.00099 86 9 4 4 3 20 0.00494 87 9 5 3 3 20 0.00593 88 10 3 4 3 20 0.00049 89 10 4 3 3 20 0.00099 90 6 7 5 3 21 0.00237 91 7 6 5 3 21 0.00949 92 7 7 4 3 21 0.00678 93 8 5 5 3 21 0.01067 94 8 6 4 3 21 0.01779 95 8 7 3 3 21 0.00508 96 9 4 5 3 21 0.00395 97 9 5 4 3 21 0.01186 98 9 6 3 3 21 0.00791 99 10 3 5 3 21 0.00040 100 10 4 4 3 21 0.00198 101 10 5 3 3 21 0.00237 102 7 7 5 3 22 0.00711 103 8 6 5 3 22 0.01868 104 8 7 4 3 22 0.01334 105 9 5 5 3 22 0.01245 106 9 6 4 3 22 0.02075 107 9 7 3 3 22 0.00593 108 10 4 5 3 22 0.00208 109 10 5 4 3 22 0.00623 110 10 6 3 3 22 0.00415 111 8 7 5 3 23 0.01957 112 9 6 5 3 23 0.03043 113 9 7 4 3 23 0.02174 114 10 5 5 3 23 0.00913 115 10 6 4 3 23 0.01522 116 10 7 3 3 23 0.00435 117 9 7 5 3 24 0.05000 118 10 6 5 3 24 0.03500 119 10 7 4 3 24 0.02500 120 10 7 5 3 25 0.12000 -
I don't have time to go into it right now. Suffice it to say that taking logs (base 10) will straighten out those curves and make the strategies clear and gives A a probability of winning of just over 60%.
That's a marvelous approach! Thanks for sharing this great puzzle and the elegant solution.
-
Thanks for a very interesting puzzle bushindo. I've thought about this one for awhile and the best I can do is a little over 71%. I'll be very curious to see how you get to over 75%.
First an observation on the puzzle and puzzles of this nature:
In any guessing puzzle like this, any individual guess can't be any better than 50%. No matter what information you get as a single player in the game, if you guess, you will only be right 50% of the time. So the key team strategy is to have as many players guess wrong when the team is wrong and only a few players to guess right when the team is right. If you pick the right strategy, the team can be right more often than not, while each individual will only bat 50%.
The first thing to think about before constructing a team strategy is to understand the distributions of the hats for 7 players. As noted in other posts you get 0 or 7 red hats 1 time each out of 128, 1 or 6 red hats 7 times each, 2 or 5 red hats 21 times each, and 3 or 4 red hats 35 times each. I can't think of any way to optimize a team strategy in a good way to account for 3 or 4 red hats. But the team can optimize for the 0,1,2 and 5,6,7 cases.
If we just look at the Brit team, they can guarantee a win if they actually have 0 or 2 total red hats and 5 or 7 red hats. Using this strategy, they lose if they have 1 or 6 red hats. The good news is there are 22*2 ways for there to be 0,2,5,or 7 red hats and only 2*7 ways to have 1 or 6 red hats for win percentage of over 75%. However they will all have to abstain more than half the time (70/128) to use this strategy.
Luckily, the other teams can pick up the slack. So, the Brit strategy is if you are told there are 0 red hats, you guess "blue." If you are told there are 1 red hats, you guess "red." If you are told there are 6 red hats, you guess "red." And if you told there are 5 red hats, you guess "blue."
For a reality check, let's add up the the right and wrong guesses, using this strategy. If there are 0 red hats, all 7 players will guess right. If there is 1 red hat, all 7 players will guess wrong. And if there are 2 red hats, only 2 players will guess right, but the other 5 will abstain. So for all the distributions, you get (7*1) + (2*21) = 49 correct guesses and (7*7) = 49 incorrect guesses. This is just as hoped for. The individuals are 50% on there guesses, but the team wins 22 times and only loses 7 times. The same is true on the other side of the spectrum with 5, 6 or 7 red hats.
The French strategy is the same as the Brit strategy, except that no one will guess if they hear that the Brits have either 0,1,2,5,6,or 7 red hats. In those cases, they know that the Brits made a guess, so they have no need to guess themselves. The French team will guess 70/128 percent of the time.
The Italians are little more complicated. First they abstain if either the Brit or French team had 0,1,2,5,6,or 7 red hats. If they know the Brits and the French abstained, they will use the same strategy outlined above with one extra case. Since abstaining is the same as losing, they should guess if there are 3 or 4 red hats. So, they should also guess "blue" if they hear that their teammates have 3 red hats. That way they will win if they have exactly 0,2,3,5,or 7 hats. The will lose if they 1,4 or 6 red hats.
The total win rate for this global strategy is: (44/128) + ((44/128)*(70/128)) + ((79/128)*(70/128)*(70/128)) = 71.63%.
If the actual optimal strategy is over 75%, I must be missing something big. I'll be very curious to hear bushindo's solution.
Thanks for the interest, howardl1963. I describe my solution below
Let's consider the 7 Brits. Let the total number of red hats be called r. The following strategy is taken from araver's post, let's hope he doesn't mind =). Let A = {1,3,4,6}, and let B = {0, 2, 5, 7}. The total number of red hat r either belong to A or to B. Given that the hat colors are uniformly assigned, A will happen 65.625% of the time, and B will happen (1 - 65.625)% of the time.
If the Brits know that the total number of red hats belong to A, then they can guarantee a win by playing with the following strategy,
Let z be the number of red hats from a person's remaining 6 countrymen, depending on z choose:
z=0 - Red
z=1 - Blue
z=2 - Red
z=3 - abstain
z=4 - Blue
z=5 - Red
z=6 - Blue
If the Brits know that the total number of red hats is in B, then they can also construct a strategy that is guaranteed to win.
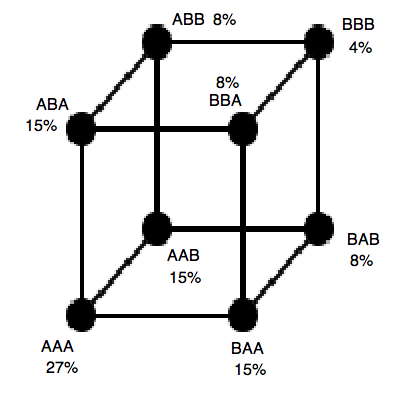
Now the game is reduced to a simple version of Essentially, we have 3 teams playing a game. Each team's state is either A (65%) or B (35%). If any team can correct guess their state, and no team incorrectly guesses it, then all wins. We can represent all possible outcomes by the following graph.
Where the letters at each vertex represent the states of the Brits, Frenchmen, and Italians, respectively. The number next to each vertex represent its probability. For instance, the probability that all there teams have state B is equal to .35 * .35 * .35 = .04 or 4%.
From the previous puzzle 'Team of 15' (see araver's excellent explanation at the end about the solution; also see for a example of a 3-person game with equal probability for the hat states), we know that given such a cube, if the 3 teams assume that their state distribution does not include ANY two diagonally opposite vertexes, then they can find a strategy that is guaranteed to win, given that their assumption is true. So, for this problem, the key is not to exclude the two vertexes AAA and BBB, as their total probability is 27+4 = 31%, giving a winning rate of 69%. If we exclude the vertexes ABA and BAB instead, then we are guaranteed to win (100 - (15 + 8) ) = 77% of the time.
-
You got quite close to the actual best winning probabilities. I must admit that I have no idea how you came up with that nice strategy. But, alas, it is possible to get a precise answer to the problem with a quite simple strategy. I am very curious as to how you came up with that 13 number set.
Sorry for the late response. I didn't internet access for the last few days. Here is how I approached the problem,
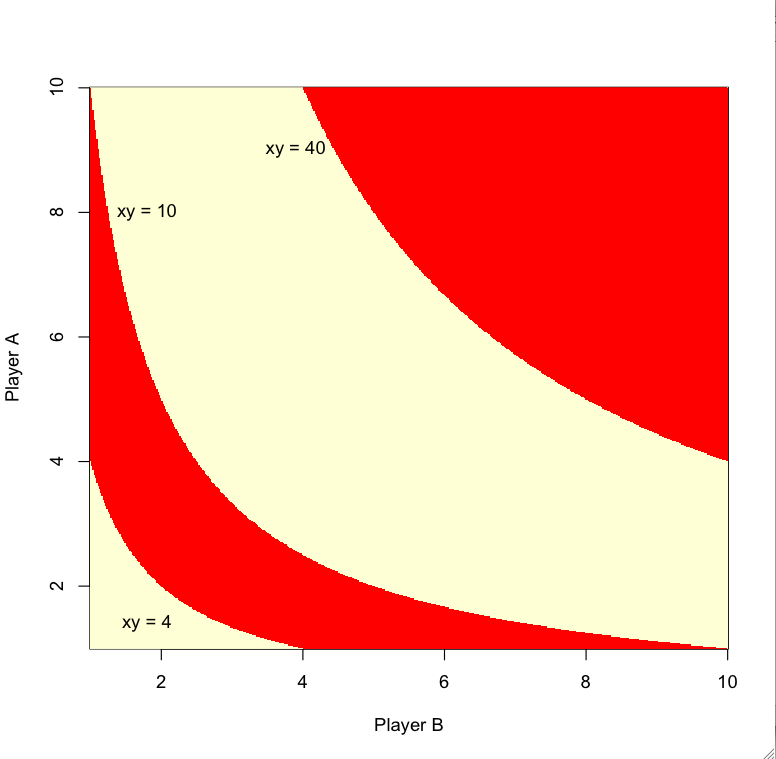
I first summarize the game with a win/loss map that plots player A/player B numbers and the corresponding outcome. As noted before, it is only necessary to consider numbers between [1, 10). In the following map, the x-axis represent player B's strategy, and y-axis player A's. The red areas are regions where player B would win. The areas are separated by three lines whose equations are displayed on the map,
So the strategy is as follows. Suppose we can only pick 5 numbers as player B, how much red 'areas' can we cover using only 5 points? I started out by picking x1 = 10 as the first number, as it can win over all numbers inside between 4 and 10 from player A (see graph below for illustration). I then project horizontal line (y=4) and see where it meets with the next red region (xy = 10), and then choose that as my next point (x2 = 2.5). The number x2 can beat numbers between 1.6 and 4 from player A. I then draw a horizontal line (y=1.6) and compute to see where it crosses the line (xy = 10). That gives me my third point x3 = 6.25. The graph below carries out the procedure for x1 to x5.
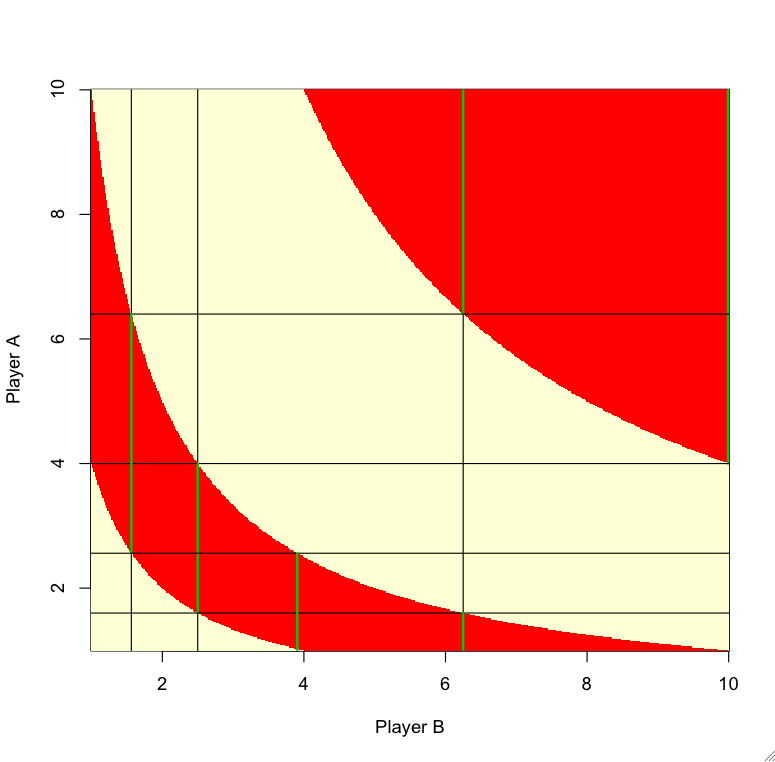
Notice that after these 5 numbers, almost every single number on the y-axis can be between by 2 out of 5 of player B's number. I'm saying 'almost' because the fifth number x5 = 3.90625 has a little bit of white areas under neath it, so the numbers interval (1, 1.024) on the y-axis is only covered once by these 5 numbers. This is not much of a problem, since we can simply add in 5 more numbers using the same procedure with a result that almost every number on the y-axis can be beaten by 4 out of 10 of player B's numbers. I cut the procedure short after 13 numbers (with the resulting winning rate 5 out of 13), but we can repeat this procedure for a longer time and get a winning rate that is approaching 2/5.
This is a wonderfully crafted problem, thanks for posting it. I would love to hear about your strategy on this problem.
-
Here is a rough stab at the strategy,
At every turn, let player B choose a number with equal probability from the following 13 number set
( 10, 2.5, 6.25, 1.5625, 3.90625, 9.765625, 2.441406, 6.103516, 1.525879, 3.814697, 9.536743, 4, 2)
It is easily shown that this strategy has a worst case winning probability of 5/13 for player B. This strategy can be improved marginally, but I think player B optimal winning rate couldn't get pass 2/5.
-
A farmer wanted to sell his goat,he took it to the animal market.
After a while came a man and asked the farmer :How many dollars is the price of this goat?
The farmer said: 100 Dollars.
The man agreed to buy it,he took the 100$ paper out of his poket in order to give it to the farmer but suddenly
the goat jumped and picked up the money and chewed it,it was impossible to save the money,the goat swallowed it down.
How can you judge between them?
The farmer doesn`t took the money, so he can not give his goat to the man,and
the man lost his money without taking the goat.
Here's a strategy to fully compensate both men
1) Let the goat owner and the buyer bring the goat to a crowded marketplace.
2) Let one of them stand on a platform and advertise to the passerby: "Raffle! Raffle! Get your raffle tickets here. Only 2 dollars per ticket for a chance to win this fabulous goat, which alone is worth 100 dollars. Not only that, we'll throw in an extra 100 dollars, in cash, for the winner of this once-in-a-blue-moon deal. Get your raffles, ladies and gentlemen. Only 2 dollars for a chance to win a goat and 100 dollars in cash! Come one, come all! Your satisfaction is absolutely guaranteed or you'll get your money back."
3) Repeat step 2) until the goat owner and the buyer have sold 100 tickets or more (income of at least 200 dollars). Then conduct a drawing and give the goat to the winner. Explain to the winner that his cash winnings are included in the goat.
4) The goat owner and the buyer then divide the income among themselves. Assuming they sold 100 tickets, the goat owner can get 100 dollars (the cost of the goat), and the buyer can get 100 dollars (the money he lost in the beginning). If the two sold more than 100 tickets, then split extra money equally and call it entrepreneurial profit.
5) If the raffle winner complains that the goat is not worth 200 dollars as advertised, let the goat owner and buyer refund the winner's 2 dollar raffle ticket and take the goat back

-
Assuming that 'falling into the black hole' means crossing the event horizon,
Simply find a supermassive blackhole. Quoting wikipedia,
"The tidal forces in the vicinity of the event horizon [of a supermassive blackhole] are significantly weaker. Since the central singularity is so far away from the horizon, a hypothetical astronaut traveling towards the black hole center would not experience significant tidal force until very deep [(way past the Schwarzschild radius)] into the black hole."
Finding such a blackhole shouldn't be hard. There is one in the center of the Milkyway.
-
Ten friends walk into a room where each one of them receives a hat. On each hat is written a real number; no two hats have the same number. Each person can see the numbers written on his friends' hats, but cannot see his own. They are given some time to ponder the numbers on the other 9 hats. The friends then go into individual rooms where they are each given the choice between a white T-shirt and a black T-shirt. Wearing the respective T-shirts they selected, the friends gather again and are lined up in the ascending order of their hat numbers. The desired property is that the T-shirts colors now alternate.
The friends are allowed to decide on a strategy before walking into the room with the hats, but they are not allowed to communicate in any way with each other once the game starts. Design a strategy that lets the friends ALWAYS end up with alternating T-shirt colors.
This is a cool problem and I'm fairly certain I've solved it. The website, where I found it, does not offer solutions of any kind, so I'm hoping someone solves it with an explanation simpler than the one I've found. Enjoy!
This is indeed a cool problem
The key of this strategy is that each participant can not tell what is the rank of his hat number in the set of 10 real numbers. He can, however, guess whether he is an odd/even number of positions from the smallest number. Combine that with a special tool that lets everybody make dependent guesses, and we got a solution.
Some general concepts are as follows. We make use of inversion numbers, which essentially tells us how out-of-order a permutation is. Each random permutation has a inversion number, which can either be odd or even. Let's label the participant from 1 to 10, the assignment of hats essentially is a random permutation of the participant's labels with respect to the hat numerical order. This random permutation has an inversion number.
The strategy is as follows,
1) Let each participant assume that the inversion number of their label permutation is even.
2) Let each participant look at the other 9 people, and construct the 10 possible permutations by inserting his position into the appropriate places (essentially by guessing that his number is the smallest, second smallest, and so on). Five of those possible permutations are even and five are odd. All the even permutation will consistently say that he is either an odd or even number of positions from the smallest hat number. If all participants follow this strategy, either they will ALL be correct about the odd/even guesses, or they'll ALL be incorrect.
3) If the result of part 2) says that a participant is an odd number of positions from the smallest number, let that participant choose a black shirt. Otherwise, choose a white shirt.
Example: Let the participants be labelled 1 to 10. Suppose that the host arrange the hat numbers so that they go from smallest to largest
( 2 , 4 , 1 , 6 , 8 ,10 , 7 , 9 , 5, 3)
Participant 2 looks at the remaining people, he sees in order from smallest to largest: (4 , 1 , 6 , 8 ,10 , 7 , 9 , 5, 3). Assuming that the permutation of 10 labels is even, there are 5 possible choices
( 4 , 2 , 1 , 6 , 8 ,10 , 7 , 9 , 5, 3)
( 4 , 1 , 6 , 2 , 8 ,10 , 7 , 9 , 5, 3)
( 4 , 1 , 6 , 8 ,10 , 2 , 7 , 9 , 5, 3)
( 4 , 1 , 6 , 8 ,10 , 7 , 9 , 2 , 5, 3)
( 4 , 1 , 6 , 8 ,10 , 7 , 9 , 5 , 3, 2)
Notice that all of these choices implies that participant 2 is an ODD number of positions from the smallest number (participant 4). Participant 2 would then choose a black shirt. If we apply the same logic to participants 1, 8, 7, and 5, we'll see that they'll get ODD positions and will choose all black shirts.
Let's look at participant 4 then, he would see in order from smallest to largest: ( 2 , 1 , 6 , 8 ,10 , 7 , 9 , 5, 3). So the five possible even permutations are
( 4 , 2 , 1 , 6 , 8 ,10 , 7 , 9 , 5, 3)
( 2 , 1 , 4 , 6 , 8 ,10 , 7 , 9 , 5, 3)
( 2 , 1 , 6 , 8 , 4 ,10 , 7 , 9 , 5, 3)
( 2 , 1 , 6 , 8 ,10 , 7 , 4 , 9 , 5, 3)
( 2 , 1 , 6 , 8 ,10 , 7 , 9 , 5 , 4, 3)
Notice that these possible permutations all state that participant 4 is an EVEN number of position from the smallest hat number. He would then choose a white shirt, as does participants 6, 10, 9, and 3. Notice that contrary to everybody's guess, the true permutation ( 2 , 4 , 1 , 6 , 8 ,10 , 7 , 9 , 5, 3) is actually ODD, however, that does not affect the fact that we get an alternating pattern anyways.
-
I'm intrigued with KlueMaster's solution with 49 cells as well. If KlueMaster could elaborate on it, that would be great.
-
Let's say we have 343 biological cells stacked into a 7x7x7 cube. In this arrangement, each cell is surrounded by a maximum of 6 neighbors. The cells can be infected with a disease. In particular, if a healthy cell is surrounded by 3 or more infected cells, it will become infected as well.
What is the minimum number of infected cells that you need in the beginning that is guaranteed to eventually infect the entire 7x7x7 cube?
-
Do you have an 'Ah-Ah' solution? I'd like to see it, if you don't mind explaining it. I enjoyed the nice 'Ah-Ah' you had for your 12 friends problem.
I just solved this Christmas problem with a boring old discrete hill-climb.
I was hoping to save the ah-ha trick for the next puzzle, but it's Christmas, no point being a Scrooge
 . Here it is
. Here it isLet the hat states be denoted by 0 and 1. Let the participants be indexed by i = 1, .., 10, and let hi represent the hat state of participant i. All the participants should assume that the following three equations are true
( h1 + h4 + h7 + h10 ) mod 2 = 0
( h1 + h2 + h5 + h8 ) mod 2 = 0
( h2 + h3 + h6 + h9 ) mod 2 = 0
Assuming that the hat states are determined by independent coin toss, the chance that the above three equations are true is (1/2)3 = 1/8. During the game, each participant will know 7 variables out of the set (h1, .., h10 ). If they substitute those 7 known variables into the above, they are left with 3 equations and 3 unknown, which is solvable. The winning rate here is 1/8.
-
If each person uses the strategy in the following table, the probability of winning
is 14/128 which gives an expected win of 167/64 gold coins/game. In the following
table, let 0 be Red and 1 be Green. Under the 7 is the color of the hat 7 away
from you on your left, 6 is the color of the hat 6 away from you on your left, etc.
Under the '|' is what color you should predict for yourself. The 1 and 2 on the
right is what you should predict for the hats one and two away from you to your right.
There are 14 winning 10-long hat assignments which win using this strategy. They are
0000000000 0011100111 0101010101 0101101011 0110101101 0111001110 1001110011
1010101010 1010110101 1011010110 1100111001 1101011010 1110011100 1111111111
left |right 7654321 012 0000000 000 0000001 100 0000010 101 0000011 000 0000100 111 0000101 110 0000110 011 0000111 011 0001000 000 0001001 111 0001010 000 0001011 011 0001100 000 0001101 001 0001110 011 0001111 010 0010000 100 0010001 001 0010010 111 0010011 010 0010100 010 0010101 110 0010110 000 0010111 101 0011000 101 0011001 101 0011010 101 0011011 010 0011100 111 0011101 010 0011110 011 0011111 101 0100000 110 0100001 001 0100010 111 0100011 001 0100100 011 0100101 001 0100110 111 0100111 010 0101000 010 0101001 101 0101010 101 0101011 000 0101100 111 0101101 011 0101110 111 0101111 111 0110000 010 0110001 000 0110010 100 0110011 001 0110100 110 0110101 101 0110110 100 0110111 101 0111000 000 0111001 110 0111010 011 0111011 011 0111100 101 0111101 001 0111110 011 0111111 000 1000000 100 1000001 110 1000010 010 1000011 000 1000100 011 1000101 111 1000110 001 1000111 111 1001000 101 1001001 110 1001010 001 1001011 010 1001100 001 1001101 110 1001110 011 1001111 001 1010000 100 1010001 010 1010010 101 1010011 011 1010100 100 1010101 010 1010110 101 1010111 111 1011000 011 1011001 111 1011010 110 1011011 101 1011100 110 1011101 000 1011110 001 1011111 001 1100000 101 1100001 001 1100010 001 1100011 110 1100100 110 1100101 000 1100110 000 1100111 001 1101000 100 1101001 010 1101010 011 1101011 010 1101100 110 1101101 000 1101110 110 1101111 110 1110000 011 1110001 101 1110010 100 1110011 100 1110100 010 1110101 001 1110110 101 1110111 110 1111000 100 1111001 001 1111010 111 1111011 111 1111100 000 1111101 000 1111110 101 1111111 111
Good work, superprismatic. Looks like the Easter Bunny is going to file for bankruptcy very soon. This puzzle didn't last that long. I'll have to think of a harder one next time.





in New Logic/Math Puzzles
Posted · Edited by bushindo
I think it is important to remember that we are limited to the availability of english words and the corresponding idiosyncratic distribution of word length. For instance,