-
Posts
719 -
Joined
-
Last visited
-
Days Won
5
Content Type
Profiles
Forums
Events
Gallery
Blogs
Posts posted by bushindo
-
-
Sorry if this has been posted before, a friend texted me this saying he needed the solution ASAP, I can proudly say I replied in a very timely manner...

Again it's that psycho warden with the obsession with hats and logic coming up with a new challenge, 3 prisoners, each gets a hat, the hats can be colored red green or yellow (no one knows how many hats in total there are of each color) each prisoner can see the hats of the other two but not his...
Each must write down the color of their hat on a piece of paper, if at least one of them is correct they all go free, what should they do?
(btw there's the usual rule if they talk or anything they all get executed, they may agree on a strategy before but that's it)
Here's how I believe the prisoners should approach this
Let Red = 0, Green = 1, and Yellow = 2. Let the prisoners be labelled by numbers 1, 2, and 3, respectively, and let the prisoners' respective hats be denoted as h1, h2, and h3.
Prisoner i should assume that the sum of the all hats modulo 3 is equal to i. That is, prisoner 1 should assume that
(h1 + h2 + h3 ) modulo 3 = 1
Prisoner 2 would then assume
(h1 + h2 + h3 ) modulo 3 = 2
And prisoner 3 assumes
(h1 + h2 + h3 ) modulo 3 = 3 = 0.
After the game starts, each prisoner should look at the remaining 2 hats and compute his own hat number (or color) from the assumptions above. One of the assumptions would have to be right, so we are guaranteed to have 1 correct guess (and 2 incorrect guesses) every time using this strategy.
-
Let's see
The witch makes a stronger poison, the wizard would drink his weak poison before even showing up for the test. He would then bring an nonpoisonous drink to the test. The witch would drink the nonpoisonous drink followed by her strong poison and then die. The wizard would drink the strong poison, nullifying his previous imbibement followed by his nonpoisonous drink.
The witch
knowing this fact, would also bring a nonpoisonous drink to the test causing the wizard to die from the weak poison he drank before he came.
But it is easy to devolve into a Wine-in-Front-of-Me situation
The witch, assuming that the wizard would poison himself beforehand, would bring a Water Potion to the test.
However, the wizard can easily flip the table by poisoning himself beforehand and bring a stronger Poison Potion. The witch can then counter that, and so on.
-
My take on this
There are the 'same' number of points on the cube as there are on the edge. That is because we can construct a 1-to-1 mapping between any point on the cube and the corresponding point on the edge.
Let (x,y,z) be the 3-dimensional coordinate of any point in the cube (surface included) where x, y, z = [0,1]. In decimal form, let's write x as
x = x0.x1x2x3x4x5... where x0 = 0 or 1 is the number before the decimal point, and xi = 0, 1, ..., or 9 for i > 0. (Of course, if x0 = 1, then xi must all be equal to 0)
Similarly, we can write y and z in the same decimal form,
y = y0.y1y2y3y4y5...
z = z0.z1z2z3z4z5...
Now, we can establish a 1-to-1 relationship between any point (x,y,z) on the cube to a point e on line segment [0, .111 ]. To do that, we can simply interleave digits and construct e from (x,y,z) as follows
e = .x0y0z0x1y1z1x2y2z2...
It is easy to see that we can reverse the process and recover a 3-D coordinate in the cube (x,y,z) given a point e. Now that we have a strict 1-to-1 matching between points on a cube to the segment [0, .111], we can do a strict 1-to-1 matching between any point e in [0, .111] and any point s in [0, 1] using a linear function
s = e * (1/.111 )
-
 1
1
-
-
Sorry, but there is an error in that proof. Assumption ~A does not imply that there is a monotone subsequence with maximum finite length M.
Suppose you are standing at a crossroads, with an infinite number of roads leading away from it. Each road is numbered with a unique natural number, and each road is n miles long where n is the number of the road. Whichever of these roads you choose (say road number p), it will eventually end (after p miles), so no road has infinite length. But you could always have chosen another road that is longer (road number p+1 for example).
The same thing could be true for these subsequences. You have proven that there is no longest monotone subsequence, but that doesn't imply that there is an infinite monotone subsequence.
Let me restate the proof in a more direct way, and we'll see if we get anywhere
Assume that there is a infinite set S, then
1) There is a monotone sequence of length 1 (Trivial statement)
2) For every monotone sequence of length K, there is a monotone sequence of length (K + 1); see Lemma from last proof.
So for any given finite monotone sequence in S of a fixed length, there is a longer monotone sequence. Therefore, there is an infinite monotone sequence in S.
-
To be more specific, you have proven that there are arbitrarily long monotone sub-sequences, but not that there are infinitely long ones.
How about this proof then,
Let A be the statement 'every infinite sequence of real numbers contains an infinite monotone subsequence'.
Let S = { a1, a2, a3, ... } be a set consisting of elements an, where n goes between 1 and infinity.
Lemma 1: Given a sequence of [(N-1)2 + 1] distinct numbers, there is a monotone subsequence of size N.
Let's assume the opposite of the A. That is, given an infinite set S, then there is no infinite monotone sub-sequence (Assumption ~A).
1) Assumption ~A implies that in an infinite sequence S, there is a monotone subsequence with a maximum finite length M. No monotone subsequence in S may have a length greater than M.
2) However, if we pick out the subsequence {a1, a2, a3, ..., a(M*M + 1) }, then we already have a monotone sequence of length (M+1) because of Lemma 1.
Since Assumption ~A leads to a contradiction between 1) and 2), then Assumption ~A can not be true. Therefore, every infinite sequence of real numbers contains an infinite monotone subsequence.
-
Show that every infinite sequence of real numbers contains an infinite monotone subsequence.
---
Sequence: a set with a specified order of its elements. For example {1-2-4-3} is a different sequence from {4-1-3-2}.
Subsequence: a subset retaining the order of the original sequence. For example {2-3-5-7} is a subsequence of {1-2-3-4-5-6-7}.
Monotone: either increasing (each number is smaller than the next number) or decreasing (each number is larger than the next number).
Let's relax the definition of monotone a bit and say that in a increasing monotone sequence, each number is bigger than or equal to than the last number. Same with decreasing monotone sequence. Then the statement in the OP is an extension of a previous puzzle
In a it was shown that in a sequence of 17 numbers, there is a monotone sequence of length 5. It is easy to extend the result there and show that for any parent sequence of length [ (N - 1)2 + 1 ], there is either an increasing or decreasing monotone sub-sequence of length N. If we let the length of the parent sequence approach infinity, then the length of the monotone sub-sequence approaches infinity as well.
-
Case A: Player selects 2 doors, one of which has a car; P[A] = 1 - (4 choose 2)/ (5 choose 2) = 2/5
Case B: Player's initial selection does not include car: 1 - P[A] = 3/5
Monty opens goat door.
In case A, one of the player's doors has a car, and both of Monty's remaining doors have goats.
In case B, both of player's doors have goats, and one of Monty's remaining doors have a car.
Case A.Stay: We are in case A, and player stays i.e. picks one of original 2 selected doors; With 1/2 conditional probability, will select car, conditional on being in case A. The net probability for pointing at right door here is 2/5*1/2 = 1/5
A.Stay.A = Pointing at right door (P = 1/5)
A.Stay.B = Pointing at wrong door (P = 1/5)
Case A.Switch: We are in case A, and player switches to one of Monty's doors; Player switches to goat with conditional probability 1, car with conditional probability 0. Net probability for pointing at right door here is 2/5*0 = 0;
A.Switch.A = Pointing at right door (P = 0)
A.Switch.B = Pointing at wrong door (P = 2/5)
Case B.Stay: We are in case B, and player stays; Player pointing at goat with condtional probability 1. Net probability for pointing at right door is 3/5*0 = 0.
B.Stay.A = Pointing at right door (P = 0);
B.Stay.B = Pointing at wrong door (P = 3/5)
Case B.Switch: We are in case B and player switches. Player points at right door with conditional probability 1/2; Net probability is 3/5*1/2 = 3/10
B.Switch.A = Pointing at right door (P = 3/10)
B.Switch.B = Pointing at wrong door (P = 3/10)
Monty opens another goat door, but let's think about this.
Monty is not allowed to open the door the player is pointing at, or the car door.
If player is pointing at the car, Monty may open any door the player is not pointing at.
If player is pointing at a goat, Monty, may not open the player's door, nor the car's door.
At this point, if player move was stay, player is pointing at right door with Prob 1/5
If player move was switch, then, player is pointing at right door with prob 3/10
If player is pointing at right door, Monty may open any of the 3 other doors. (Depending on strategy choice, we can make the probability of this case 1/5 or 3/10).
If player is pointing at wrong door, Monty may only open 2 of the other doors (since one of the other 3 is as car). (Depending on strategy choice, we can make the probability of this case 4/5 or 7/10).
Most likely to win if player is wrong at this point, and Monty gets rid of another goat.
If wrong, and Monty get's rid of another goat, then switch to one of 2 other doors, one of which is the car.
To maximize chance of being wrong at this point, should stay at first opportunity(P[wrong] in that case is 4/5), then switch at 2nd choice (P[win|was wrong] = 1/2).
With this strategy the probability of winning is 4/5*1/2 = 2/5.
To summarize, strategy is pick 2 of the 5 doors at random. After Monty opens a goat door, choose randomly of the 2 doors you initially picked.
After Monty opens another goat door, choose randomly of the other two that remain (not the one you were just pointing at). You will win 2/5 times regardless of how Monty picks doors and whatever his motives are.
Great analysis, and I agree with your answer. Good solve.
-
Try a right circular cylinder with height = 2R, made of the same material at the same T and P.
Yes, you can assume initial conditions of R0, t0, etc.
I get the same results with a right cylinder as with the sphere
We first assume that the right cylinder holds its cylindrical shape as it sublimates. The Area and Volume of the cylinder are
A = 6 pi r2
V = 2 pi r3
The given differential equation is
dV/dt = k * A = k * ( 6 pi r2 )
We can compute dV/dr as
dV/dr = 6 pi r2
We convert dV/dt into dr/dt using the above, and we get
dr/dt = k
So the change in radius with respect to time is a constant k, which implies that the half-sublimated and fully-sublimated times are (1/2)* R0/k and R0/k, respectively.
-
I had got the same answers as you... but would like to see how you had worked it out...
Here's the integral I used for Case 1,
The first and third terms on the right hand side actually evaluate to the same value, but I kept them distinct since it makes it easier to follow the logic.
I like bonanova's approach much better though.
-
There are two friends, who decide to meet at a place between 5 PM to 6 PM everyday. What are the chances that, on a given day, they will be able to meet. Provided-
Case 1: They agreed whoever comes first, will wait for 15 minutes for another friend to arrive.
Case 2: One friend wait for 10 minutes and other for 20 minutes for another friend to arrive.
And which of the above two cases holds better chances of there meeting ?
Assuming the arrival time for the two friends are independently, identically, and uniformly distributed over the hour, then
The probability of meeting can be computed as a sum of simple integrals. The probability of meeting for case 1 is 7/16 = 0.4375, and the probability for the second case is 31/72 = 0.4305556. So case 1 has a slightly higher meeting chance.
-
let heads be 1 and tails be 0. can you flip a coin enough times to form an irrational number?
This puzzle statement may be undercontrained,
Let fi be a binary variable representing the i-th coin flip. There is an extra parameter that is required to form a number from the sequence of fi. Consider the following equation for using fi to generate the natural numbers, AN, from N coin flips
or this equation to use fi to generate a random number between 0 and 1
Both of these methods return rational numbers for all N, but both of the above implicitly uses a factor of 2 in constructing the number AN. There is nothing that really requires us to use 2, though. We can easily define a number generating scheme that returns an irrational number as follows
Under the scheme above, we are guaranteed to get an irrational number with any finite number of coin flips.
-
But, if the person Zeta (or his/her heirs or assigns) will start by removing the ball numbered N, Alex will only be able to add to the N-1s. While Zeta removes N-1s, Alex is constrained to N-2s. As soon as Zeta's team starts on the Ms, Alex is constrained to M-1s, and can never go higher. Eventually, when Zeta's team is working on 2s, Alex is stuffing the bucket with 1s. But once Zeta's team starts working on 1s, Alex has to sit by and twiddle his/her thumbs.
Aye, Captain,
Let's look at the strategy where we remove the highest numbered ball at every turn. Let's define Alex's decision function as f(i, j), which is a integer-valued function that returns the number of balls that Alex would add on the j-th time that the player removes a ball numbered i. The function f(i,j) can be arbitrarily large, but it must still be a well-defined function. Also, note that f(1,j) = 0 for all j, since Alex does not have any ball labelled '0'.
Define Ti as the maximum possible number of balls with the number i that would be in the bag under this strategy. It is easily to see that we can write a recursive function for Ti-1 given Ti:
where TN = 1. So, given a finite N number of balls at the beginning, and an integer-valued decision function f(i,j), we can derive the ultimate maximum number of balls of any label. The function f(i,j) may be arbitrarily large; for instance, we could imagine a case where f(i,j) = 101000, which within 1 turn would result in the bag having more balls than the number of atoms in the observable universe. However, in theory, the recursive function above have finite number of terms, and so the drawing process should come to an end eventually.
-
that for each digit in the binary representation, if your coin flip is not the outcome representing the digit, you stop. So 50% chance of needing another coin flip at any point in the process.
So there's a 50% chance of it taking only 1 flip.
There's a 25% chance of it taking 2 flips.
There's a 12.5% chance of it taking 3 flips.
etc.
So the infinite sum for the average flips needed is the sum from i=1 to infinity of i/(2^i).
f(y) = sum x=1 to inf xy^-x
f(y)/y = sum x=1 to inf xy^-(x+1)
integrate (f(y)/y) + c = sum x=1 to inf -y^-x
-integrate (f(y)/y) + c = (1/y)/(1-(1/y))
-integrate (f(y)/y) + c = (1/y)/((y-1)/y)
-integrate (f(y)/y) + c = 1/(y-1)
integrate (f(y)/y) + c = -1/(y-1)
f(y)/y = d(-1/(y-1))/dy
f(y)/y = d(-(y-1)^-1)/dy
f(y)/y = (y-1)^-2
f(y) = y(y-1)^-2
Plugging in 2 for y gives f(y)=2.
So it takes 2 flips on average.
Of course, it would be easier to formulate it this way...
All need at least 1 flip.
50% need at least an additional 1 flip.
25% need at least an additional 1 flip.
etc.
So 1 + .5 + .25 + .125 + ... = 2.
Great solve. It is indeed surprising how efficient bonanova's and your algorithm is.
-
A while back we discussed the interesting process where each step consisted of placing consecutively numbered balls into a bucket, two at a time, and then removing the lowest-numbered ball. We postulated an infinite number of balls being processed in this manner. Completion was "ensured" by executing each step after an interval of time that was one-half of the interval of the previous step. An Infinite number of steps could thus be executed in finite time, after which the bucket could be inspected.
The puzzle was to describe the final contents of the bucket. The unintuitive result is that it would be empty. Even though after each step the number of balls it contains increased by one.
The interested reader can enjoy my misguided discussion of the outcome here.
We propose here a different kind of very long task, also involving placing and removing balls into and from a bucket. Completion is again the central issue, and the bucket's final contents if it's the case that the task does in fact complete. Nothing in this task is infinite, but it is unbounded.
You are given a bucket that contains an arbitrarily large number N of balls, numbered 1-N. You are to empty it, by a series of steps described below. To make the task interesting, an adversary named Alex tries to prevent you from emptying the bucket. Alex is well equipped to prevent your success. For each numbered ball initially in your bucket, Alex has another bucket with an infinite number of balls marked with the same number. That is, if your bucket initially contains a ball that is numbered 37, Alex has his own bucket with an infinite number of balls also numbered 37.
Here is how the steps are executed. You remove a ball of your choosing, say its number is p, and discard it. Alex may then add to the bucket an arbitrarily large number of balls numbered p-1, using his infinite bucket of p-1 balls. An individual step can thus add to your bucket a set of new balls of size equal to the number of electrons in the universe. Moreover, your bucket might have started with that many balls initially. But even if your bucket starts with as few as 2 balls, it is not possible to place a bound on the number of steps needed to empty the bucket.
So here's the question: Can you empty the bucket?
Some clarification please. What happens when the player removes a ball labeled with the number 1?
-
I thought I'd include it even though it's similar to what bonanova posted.
Take the binary representation of the probability of a head coming up that you are trying to emulate. If you let heads be 0 and tails 1, start flipping the coin and once you have a different outcome than in the binary representations stop. If you got a heads instead of a tails, the emulated outcome is heads. If you got a tails instead of heads, the emulated outcome is tails.
Now that bonanova and EventHorizon have posted solutions to the original problem, allow me to pose an extension. What is the average number of coin flip required for bonanova's and EventHorizon's approach to sampling the probability p? Extra bonus for putting the answer in closed form (i.e., without requiring an infinite sum).
-
I thought about the point you're making, but I didn't come to precisely that conclusion. A fair coin requires ony a single flip to give a p=0.5 outcome. By comparison, this scheme can take an arbitrarily long sequence of flips. But only in a vanishingly small fraction of cases. That's the only "finite N" limitation that I see. Almost every "finite N" sequence of flips is sufficient to produce the desired result.
As to whether the scheme produces the exact bias of p, I think it does.
You'd have to run the scheme an arbitrarily large number of times to reconstruct [verify?] the value of p that defines its bias, just as you'd have to do with a fair coin to prove that it's fair. But the bias produced by the scheme, each time it's run, is precisely p.
You're right in that your scheme, which calls for consecutive flips until the outcome differs from the binary representation, returns a probability that is precisely p. I made a mistake earlier in saying that my scheme (flip the coin for a fixed number of time N) is 'equivalent', which it assuredly is not. While that scheme may be more intuitive, it sufferers from approximation error due to the fixed finite N, plus the fact that it is not as computationally efficient. Good point!
-
Thanks for raising above concerns... I assume, I framed the problem in bit hurry... here are the clarification to your concerns...
AIM is to minimize average waiting time...
Further assume, it's a residential building... all residents mostly travel between their floor and ground floor, so please ignore other in-between floor travels...
Hope this problem make more sense now...
Thanks for the clarification. If that's the case,
Assuming no net gain or net loss of residents, the probability of call from floor 0 is 1/2, while probability of calls from each remaining floor is 1/24. The 2 elevators should idle at floor 0 and floor 8.
-
By 'ideal distribution of elevator position', do you mean that
1) You wish to minimize expected the number of floors it would take for an elevator to reach a caller whenever he/she presses the elevator button?
2) Or do you wish to minimize the expected total distance that an elevator would travel when requested (i.e., caller A request the elevator from floor i to go to floor j; the nearest elevator travels from its idle floor to floor i, takes the caller to floor j, and then return to its idle floor)?
Also, as it is, the problem is under-constrained since it leaves out an important piece of information, which is the probability of calls from the ground floor (or floor 0). Consider the following two scenarios
A) Nobody in the building travels to the ground floor. All calls from floor 1 to 12 are equally likely, and each elevator trip travels to floor 1 to 12 with equal probability. In this case, probability of calls from the ground is 0.
B) All building residents only travel from their floor to the ground, and from the ground to the their floor. Assuming that there is no net gain or loss in the number of residents, then probability of calls from ground floor is 1/2.
Both scenarios A and B satisfy the OP, but they have different implication on the resulting `optimal' idle floor. Some clarification would be appreciated.
-
I was incorrect in the post above. Turns out we don't really need the prior distribution of the red balls. In the words of CaptainEd, "Durn, hit by Bayes again" :-)
-
A bag contains two blue balls and an undetermined number of red balls.
A ball of unknown (red or blue) color is added to the bag.
Finally, a ball is drawn at random from the bag.
If the drawn ball is blue, what is the probability that the added ball was red?
I think the crux of the puzzle lies in the part that is highlighted red above. I assume that by 'undetermined number of red balls', you mean that the precise number of red balls is unknown. However, the solution to the puzzle requires that we assume something (a priori information) about the generating distribution of the red balls (e.g., poisson distribution, exponential distribution, gamma distribution, etc.). We could also start going into improper priors, but I'd rather not =). This puzzle seems dangerously close to a subjective argument about what type of prior distribution does 'undetermined number of red balls' mean, maybe the OP can clarify that a bit?
-
Yup, that's essentially what I got.
What's interesting is combining the last puzzle and this one you can show that with any biased (or fair) coin you can emulate any other biased (or fair) coin or any die of any number of sides. I didn't include emulating a biased die, but that's not much of a stretch. (this does assume both heads and tails can and do occur)
I thought I'd include it even though it's similar to what bonanova posted.
Take the binary representation of the probability of a head coming up that you are trying to emulate. If you let heads be 0 and tails 1, start flipping the coin and once you have a different outcome than in the binary representations stop. If you got a heads instead of a tails, the emulated outcome is heads. If you got a tails instead of heads, the emulated outcome is tails.
You can actually extend this directly to emulating any biased (or fair) coin or die with any other biased (or fair) coin (or die, as you can emulate a biased coin by trivially rerolling if one of two selected outcomes don't come up) that you know the outcome probabilities for. If you don't know it's probabilities, emulate a fair coin first, but then it's not quite direct.
You just need to partition the space on a number line from 0 to 1, giving each outcome to be emulated the space corresponding to the probability it should occur. Start with the whole space, [0,1]. Subdivide the space according to the probability heads comes up in the coin you are using. So the ratio of the length representing heads to the length representing tails is the ratio of heads to tails in the probability of the biased coin you are using. If heads comes up, repeat using the portion currently representing heads. Similarly for tails. Once you have subdivided small enough that the whole length is within the partition representing one emulated outcome, that is the outcome to use.
Great puzzle. I'd just note that there's equivalent way to do this that may be more intuitive for some people.
Let p be the probability (in decimal notation) you want to simulate. Cast the fair coin N times and then treat the N-digit outcomes as a binary number. Convert that binary number into decimal number, call it O.
If O > p, call it a Failure. If O < p, call it a Success.
Another note is that in general this scheme does not precisely equate to p for any finite N. Asymptotically, it should converge to p though.
-
okay once more...
prisoner 1x drinks from the bottle if bits 1 2 4 5 7 9 result in odd by xoring them together.
2x drinks if bits 1 3 4 6 7 result in odd by xor.
3x 2 3 4 8 9
4x 5 6 7 8 9
so, if prisoners 1 and 8 die, all four extras die.
let's say 2 also dies but is the false poison.
1x 2x 1 3x 2 3 4 4x 5 6 7 8 9
1 1 1 1 1 0 0 1 0 0 0 1 0 = 1 = dies, 0 = live
if you xor the same bits for each prisoner, you see that 1x is wrong, and 3x is wrong.
1 +4 = 5, the 5th bit is 2. therefore 2 is the poisoner.
if 5 was the false poisoner, you have prisoner 1x and prisoner 4x wrong. 1+8 = 9, with the 9th bit being 5.
Congratulations, you got it. Great solve.
-
i believe i can do it with 13.
as before, label the bottles 1-500 in binary and assign 9 prisoners each binary bit for drinking.
then with the four extra prisoners, prisoner 1x drinks the bottles prisoners 1, 3, 5, 7, and 9 have drinken from.
(the bottles with any odd bits set.)
prisoner 2x drinks the bottles prisoners 2,3,6,7 have drinken form.
prisoner 3x drinks the bottles prisoners 4,5,6,7 have drinken from.
prisioner 4x drink the bottles prisoners 8,9 have drinken from.
in this way, the four extra prisoners act as a a parity check of the 9 drinking prisoners.
as an example... let's say the acomplice is prisoner 7.
we get a result of prisoners 1, 3, and 7 dieing. this tells us that bottle 2^6 +2^2 +1 = 69 is likely poisoned.
however, only prisoner 1x and 2x die. therefore 7 was the accomplice
let's say the acomplice was 4x. let's say 3,5, and 7 die. this tells us that 2^2 +2^4 +2^6 = 84 is likely poisoned.
prisoner 1x, 2x, 3x, and of course 4x dies. since all 4 of them had no drinks in common, you know one of the extras was the accomplice. therefore the 84th bottle was poisoned.
Question regarding this approach
The solution seems to add 4 prisoners, where
prisoner 1x drinks the bottles prisoners 1, 3, 5, 7, and 9 have drinken from.
prisoner 2x drinks the bottles prisoners 2,3,6,7 have drinken form.
prisoner 3x drinks the bottles prisoners 4,5,6,7 have drinken from.
prisioner 4x drink the bottles prisoners 8,9 have drinken from.
So, suppose that prisoner 7 and prisoner 8's allotted drinks include the poison, and they both die. From the scheme above, the prisoners 1x, 2x, 3x, and 4x will die as well.
Suppose prisoner 7 and prisoner 8 have the poisoned wine among their drinks, this scheme seems like it can not distinguish between the cases where the the accomplice is among the remaining non-parity-check prisoners (i.e., prisoner 1, prisoner 2, and so on).
-
Four extra prisoners can correct a single faulty bit for up to 2048 bottles.
So long as they're hamming it up a bit as they drink.
All correct there, except for one detail
9 + 4 = 13 prisoners won't be enough to correct a faulty bit up to 2048 bottles. You will need more prisoners for that many bottle.
The emperor would also like to request more details on this drinking scheme for the sake of completeness. You see, back in college the emperor majored in Political Science, which does not require any course in Computer Science, so concrete details on how to go about doing it would be very much appreciated.
-
 1
1
-


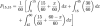

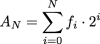
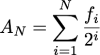
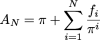
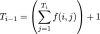
No need to answer
in New Logic/Math Puzzles
Posted
You people are making this too complicated =) Let's say that a speaker wants to convey the statement "I want dinner now".
If the speaker is type B, he should ask "Is the sentence 'I want dinner now' grammatically incorrect?"
If the speaker is type A, he should ask "Is the sentence "I want dinner now' grammatically correct?"
There might be some work getting all the denizens familiarized with this convention, but the bonus is that once established, the convention does not require a speaker to first identify whether he is type A or type B.