-
Posts
719 -
Joined
-
Last visited
-
Days Won
5
Content Type
Profiles
Forums
Events
Gallery
Blogs
Posts posted by bushindo
-
-
This is based on bonanova's puzzle
Here's a game that goes as in the following
* There is a host with 14 stamps, 7 red and 7 blue. There are five players- A, B, C, D, and E.
* In the beginning, the host affixes two stamps to each of the 5 players' head. The remaining 4 stamps go into the host's pocket. Each player can see the stamps on the remaining 4 players, but can not see his own stamps nor the four in the host's pocket.
* Starting from A to E (and then looping back to A and so on), the host asks if each player definitively knows his stamps distribution (RR, BB, or RB). If the player does not know, the host goes on to the next player. No guessing is allowed.
* The game goes as follows
1st turn- player A: I do not know
2nd turn- player B: I do not know
3rd turn- player C: I do not know
4th turn- player D: I do not know
5th turn- player E: I do not know
Host- Alright, to help you, I'll now reveal two stamps from my pocket. *At this point, the host pulls out two of the four stamps in his pocket and shows everyone. The game then continues as before*
6th turn- Player A: I do not know.
…
Question- what is the longest possible number of turns required before a player definitely knows his color? -
As stated in the OP any audience member who is not a truth-teller or a liar will randomly lie or tell the truth. If you like, s/he could make that decision by coin flip.What kind of 'random' are the random answerers? Do they, like, flip the coin every time they answer or is there a pre-set random order of truth/lie that they have memorized? Also what happens when you ask someone a question they cannot answer?
...would be something like: Ask the entire audience "if I asked you N questions, then for the (N+1)th question asked you 'Is the money in the left door?', would you answer yes?"Truth tellers and liars will both give you the truth, random answerers will not be able to answer.
Clarifications, please
1) Does each member of the audience know the type of all remaining audience member?
2) For the audience members that randomly tell the truth or lie, at any moment, do they know whether they will lie or tell the truth to the next question? That is, before hearing a particular question, have they already decided on lying or telling the truth?
-
Let P(n) be the probability of going bust, starting with N dice, where a die is said to go bust if all of its descendants go bust. The descendants of a die are those dice that are put into the gambler's stake after a successful wager, and (recursively) the descendants of those dice.
I believe P(2) = P(1)^2, because in order to go bust with both dice, each die needs to go bust, and they are independent.
Similarly, P(3) = P(1)^3.
So, what is P(1)?
P(1) = 1/4 (1 + P(1) + P(2) + P(3))
= 1/4 (1 + P(1) + P(1)^2 + P(1)^3)
so 3P(1) = 1 + P(1)^2 + P(1)^3
P(1)^3 + P(1)^2 -3P(1) + 1 = 0
The roots of this equation are 1, sqrt(2)-1, and sqrt(2)+1.
In the interval of interest, we have two roots: sqrt(2)-1 and 1.
I'm inclined to rule out 1 (without good justification--this is infinity we're talking about...), yielding a probability of (eventually) going bust of 0.414.
Good solve, CaptainEd. Nice and compact solution =)
-
You glue two small square pyramids together at their bases to form an eight-sided object that becomes a fair die. You mark the opposite pairs of faces with 0 1 2 and 3.
You begin the game with $1. You roll the die; the number that shows is your new stake. That is, with equal probability you lose you dollar, you keep your dollar, you double your dollar or you triple your dollar.
A minute later, you bet each of your dollars, if any remain after the first roll, with another roll of the die; one roll for each dollar that you have, and collect your winnings, if any. After another minute passes, each of your dollars, if any, suffers the fate of another roll. To be clear, in all cases each dollar is wagered individually. As the minutes turn into years, you eventually become rich, or you go bust.
What is the probability that you go bust?
I like the conditions that Prime gave in his last game. You can simulate the game if you like. But a submitted solution must comprise an answer and a method, both of which are correct. Enjoy!
Here's an approach
Define P(N) as the probability of going bust if you currently have N dollars. Obviously, P(0) = 1, and the quantity of interest is P(1). Note that P(N) for large N should be approaching 0.
The procedure to find P( 1 ) is as follows,
Construct a series of equations for P(N) as in the following
P(N) = a0 * P(0 ) + a1 * P(1 ) + a2 * P(2 ) + … + an P(N)
where an is easily defined based on the properties of the rolling dice. For instance, the first 3 equations will be
P(1) = (1/4) * P(0 ) + (1/4) * P(1) + (1/4) * P(2 ) + (1/4) P(3) P(2) = 0.0625 * P(0 ) + 0.1250* P(1 ) + 0.1875* P(2 ) + 0.2500* P(3 ) + 0.1875* P(4 ) + 0.1250* P(5 ) + 0.0625 * P(6 ) P(3) = 0.015625* P(0 ) + 0.046875* P(2 ) + 0.093750* P(2 ) + 0.156250* P(3 ) + 0.187500* P(4 ) + 0.187500* P(5 ) + 0.156250* P(6 ) + 0.093750* P(7 ) + 0.046875* P(8 ) + 0.015625* P(9 )
The key now is that we will assume P(N) = 0 for N >= 30. This is a reasonable assumption because a rough order-of-magnitude guess for P(30) = (1/4)^(30) = 8e-19, so that's close enough to zero.
So, we we construct 30 equations P(N) for 0 <= N <= 29 as described above. This system of 30 equations can be rewritten as a matrix equation
A * p = p
where A is a matrix constructed about of the coefficients an, and p is the 30-dimensional vector (P(0), P(1), P(2), … , P(29 ) ).
p is obviously an eigenvector of A corresponding to the eigenvalue 1. It is then straightforward to find p using eigen decomposition. The value for P(1) is .4142136. The bust probabilities for all starting dollar values between 1 and 29 are
[1] 4.142136e-01 1.715729e-01 7.106781e-02 2.943725e-02 1.219331e-02 [6] 5.050634e-03 2.092041e-03 8.665518e-04 3.589375e-04 1.486768e-04 [11] 6.158394e-05 2.550890e-05 1.056613e-05 4.376635e-06 1.812861e-06 [16] 7.509115e-07 3.110374e-07 1.288356e-07 5.336514e-08 2.210427e-08 [21] 9.155624e-09 3.792164e-09 1.570594e-09 6.504336e-10 2.693280e-10 [26] 1.114981e-10 4.614419e-11 1.908862e-11 7.891683e-12
-
 1
1
-
-
I came across this somewhere on the web.
A pawn is sitting at one corner of an 8X8 chess board. It can take one step at a time in the horizontal or vertical direction (not diagonal). What is total number of ways in which it can reach the diagonally opposite end given that the pawn always tries to go towards the destination (i.e. no back-tracking).
I came up with an answer. Wanted to see whether it is the correct approach. Thank you
Hope you will enjoy
My guess
Let's say that the pawn is in the lower left corner. It has to go up 8 times and right 8 times to get the the other corner. This makes the total number of ways 16C8 = 12870.
-
Nine white poker chips have the numbers 1, 2, 3, ..., 8, 9 written on them, one number on each chip. You and a friend alternately select a chip, with the aim of being the first to draw three numbers that sum to 15. You may play first or second. Do you have a winning strategy?
Here's a winning strategy
Pick to be the first player and choose 5 as the first number. Let the second player's first choice be S.
If S is 1, 9, 2, 6, or 7, then player 1's 2nd, 3rd, and 4th moves should be among the following set (3,4,8)
If S is 3, 4, or 8, then player 1's 2nd, 3rd, and 4th moves should be among the following set (2, 6, 7). The key is that after playing S, player 2 would be constrained to block player 1's move from getting 15.
Example. Let say player 1 choose 5, and player 2 chooses 2. The game would go as follows
Player 1- 1st choice: 5
Player 2- 1st choice: 2
Player 1- 2nd choice: 3
Player 2- 2nd choice: 7 (have to choose 7 to prevent a player 1 win)
Player 1- 3rd choice: 4
Player 2- 3rd choice: 6 (have to choose 6 to prevent a player 1 win)
Player 1- 4th choice: 8 (WIN- 3 + 4 + 8 = 15 )
In this example, doesn't 2nd player win on his 3rd move having (2,7,6)?
Shucks, back to the drawing board.
-
But they don't need to be integers, those 11 periodic values.
As long as we have 11 periodic values, we could plug them, say, into
Lagrange Interpolating Polynomial to produce integer values of our choice like [0,1,2,3,4,5,6,7,8,9,10].Tangent seems like a good choice for a periodic function. We could plug tan(N*pi/11 - 21pi/22) as "x" variable into our Lagrange Polynomial, [tan(-21pi/22), tan(-19pi/22),...,tan(21pi/22)] as xk points and [0,1,...,10] as yk points. Subtract that from N, divide by 11, and voila. I am not constructing the actual formula. The main thing I seem to remember about the Lagrange Interpolating Polynomial from the time when my daughter took all those AP math classes at high school, that it's big.
Anyone, be my guest and work out the details for half of my "best answer" credit.

Excellent answer
The key of the puzzle is indeed to construct 11 linearly independent terms, taking advantage of the cyclical nature of trig functions. It is then easy to construct a linear combination of the 11 terms so that they combine to be within the set [-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5]. It is then straight forward to construct a closed form solution using linear algebra.
-
Nine white poker chips have the numbers 1, 2, 3, ..., 8, 9 written on them, one number on each chip. You and a friend alternately select a chip, with the aim of being the first to draw three numbers that sum to 15. You may play first or second. Do you have a winning strategy?
Here's a winning strategy
Pick to be the first player and choose 5 as the first number. Let the second player's first choice be S.
If S is 1, 9, 2, 6, or 7, then player 1's 2nd, 3rd, and 4th moves should be among the following set (3,4,8)
If S is 3, 4, or 8, then player 1's 2nd, 3rd, and 4th moves should be among the following set (2, 6, 7). The key is that after playing S, player 2 would be constrained to block player 1's move from getting 15.
Example. Let say player 1 choose 5, and player 2 chooses 2. The game would go as follows
Player 1- 1st choice: 5
Player 2- 1st choice: 2
Player 1- 2nd choice: 3
Player 2- 2nd choice: 7 (have to choose 7 to prevent a player 1 win)
Player 1- 3rd choice: 4
Player 2- 3rd choice: 6 (have to choose 6 to prevent a player 1 win)
Player 1- 4th choice: 8 (WIN- 3 + 4 + 8 = 15 )
-
No, I won't try it myself.
But could your from RG's puzzle be generalized, by replacing "3"s with "11"s?
Comments
Indeed that trig expression could be generalized, although the particulars are a bit more involved than replacing '3's with '11's. The devil is in the details =)
-
This is based on a previous
Find a closed form expression for function f(N) such that
f( N ) = 0 for 1 <= N <= 11
f( N ) = 1 for 12 <= N <= 22
f( N ) = 2 for 23 <= N <= 33
f( N ) = 3 for 34 <= N <= 44f( N ) = 4 for 45 <= N <= 55
...
No modulus or rounding operators are allowed. -
Prime, that analysis is convincing. Consider the following as well.
I wonder, in light of your betting on "1" appearing in just four die rolls
means we should be looking at median outcomes rather than average.
Since dice rolls are independent, rolling
m dice once and one die m timeswill give indistinguishable results.
OP thus asks:
On average, how many rolls of a single die are required to get all six results?
Betting on a smaller number loses, on average; a greater number gives a win.
The "waiting time" to expect a particular result [measured in actual time, or (more often) in number of trials]
is simply the reciprocal of the probability of obtaining the result in unit time, or in a single trial.
In the present case the reciprocal probabilities for the 1st, 2nd, 3rd, ..., 6th distinct value to appear are, trivially,
1, 2.2, 3.7, 5.7, 8.7, 1 2.20138 3.70155 5.69817 8.70078 14.70568
On the other hand, all six values appear more than half the time in 13 rolls of a die.
I agree with the note about median. I think the problem here is that the OP and post 14 (see blue-colored part in spoiler above) are conflating the median and the average (or mean) in the interpretation of the winning condition
Let's adopt Bonanova's convention and reframe the OP as a problem of rolling a single die N times. Let P( N ) be the probability that all 6 numbers cummulatively show up *on precisely* the N-th roll (i.e., the winning condition is *first* satisfied on the N-th roll). The OP and the post 14 poses actually two different problems
1) OP: What is smallest value of N that gives you a winning bet on average? I think a reasonable interpretation of this is that what is the smallest N such that the cumulative probability of winning is above .5. In mathematical notations, we are looking for the median M, which is defined as the smallest M such that
2) Post 14: On average, how many rolls of a single die are required to get all six results?
This definitely asks for the expected value of the number of rolls required to get 6 different numbers. In mathematical notation, we are looking for the average A
The key here is that for this puzzle, the median is roughly 13, while the mean is roughly 14.7.
-
This problem recently popped back into my head. In one of my college calculus classes while working on sequences we came across the sequence 0,0,1,1,2,2,3,3,4,4,... and if I remember correctly we were told there was no closed form equation for it. But, I found one and presented it to the class.
a[n]=(2n-1+(-1)n)/4 n=0...infinity
My question is: Is there a closed form equation to define the sequence 0,0,0,1,1,1,2,2,2,3,3,3....? If not, why not?
Just wondering.

Here's one that doesn't use floor or mod
-
This is great - beautiful, even.Let T be the square root of 2. Consider the infinite continuedexponential, X=T^(T^(T^(T^(T^..... What is X? Well, we clearlyhave X=T^X. X must be 2 because 2=sqrt(2)^2. Also, X must be 4because 4=sqrt(2)^4. Ergo, 2=4. Dividing both sides by 2 gets1=2. QED
Except, the power tower unfortunately does not converge for both cases (for 2, but alas not for 4 as I remember.)
I made a graph of the divergence point sometime back, I will look for it.
When the records are written, however, this def gets Honorable Mention.
Great proof as well. I have no beef with the power tower, but isn't the argument similar to this one
Let's say that a variable x satisfies the following relationship,
x^2 - 6x + 8 = 0
Since x=2 and x=4 both satisfy the equation, then 2 = 4, or 1=2. It should be easy to find the weak point now.
-
I'm taking a slightly stricter view, that NEWS coding is not available.
Wolfgang has allowed that prisoners can either face toward or away from the door.
That is, NS (or EW, as I drew it) coding is available, and that requires two prisoners to signal a color.
That presents a particular problem for P2 on initial entry, but I think it can be worked around.
If only a binary signaling scheme is allowed, CaptainEd has shown that only prisoner 1 needs to change his mind. Even in the stricter NS view, there are some latitude to define a quadnary signaling scheme due to an implied necessary condition
the entering prisoners *must* be able to see the signaler rotate before taking their position. Otherwise, the last prisoner has no way to receive information about his hat color, and the puzzle is not solvable. Therefore, rotation *within sight* of entering prisoners is a necessary condition of the puzzle.
Since the entering prisoners are able to see rotation, it is then trivial to combine rotation speed, direction, and amount with NS coding to allow quadnary signals. (Again, I don't see anything in the OP prohibiting this; well, except for the 'no communication of any kind allowed', but we all know how that went). Once quadnary signals are allowed, no one needs to change position.
-
We will prove a more general result using a simple induction argument.
We prove: Any set of numbers are all equal.
Proof:
(Base Case) -- If we have a set consisting of one number, it is clear
that all the numbers in this set are equal.
(Inductive Step) -- We assume that any set of N numbers are equal.
Now, we will show that any set of N+1 numbers are all equal. Let us
take one number out of the set of N+1. We are now left with a set
of N numbers and, by our induction hypothesis, all N of these are
equal. So, we put the number we took out (call this number X)
back in the set to again make it a set of N+1 numbers. We now
take a different number out of this set (call this number Y).
Now, we once again have a set of N numbers which, by the induction
hypothesis, have all equal numbers. The only way this can happen
is if X=Y because each of X and Y are equal to the other numbers in
the set. So, any set of N+1 numbers must all be equal.
(Therefore) By induction, any set of numbers must contain numbers
which are all equal.
In particular, the set {1,2} must contain numbers which are all
equal. Thus 1=2.
Counter example to this proof =)
We use the same set- {1, 2}. Following the reasoning above, then
X = 1
Y = 2
but it doesn't follow that X = Y. I guess N=2 is the weakest link of this induction chain.
-
your method is successful with the first two prisoners, but you should find a very simple,uncomplicated way for the 3rd one,if you find it, the rest will be very easy and straight forward job.
How about this *very easy and straight forward* method?
Let's index the prisoners by the order in which they enter the room. Let prisoner 1 be the communicator that signals the hat color of all subsequent prisoners as they enter. We can signal the hat color by degree of turning. Let a 90-degree clockwise turn be Yellow, 180-degree turn be Green, 270-degree clockwise (or 90-degree counterclockwise) turn be Red, and 360-degree turn (or not turning at all) be Blue.
Let's index the invisible rows by numbers -4 to 4. Prisoner 1 stands at row 0 and start signalling at the others prisoners as they enter. The subsequent prisoners can take on the corresponding row depending on prisoner 1's color in order that the rows form a (Yellow,Green,Red,Blue) sequence.
The great thing about the above is that prisoners 1 and 2 *do not* have to change chosen positions at all. This assumes that prisoner 1 can rotate *within sight* of entering prisoners (don't see anything prohibiting this in the OP).
-
I can add something which may help you... The raws may face the door or the opposit direction!
Continuing with the community solve approach, can we clarify:
- Must all the persons in a particular row face the same direction?
- If prisoners in say the Yellow row can face in differing directions does that constitute [illegal] communication?
- Can the first two prisoners choose the time that they [legally] alter their position, at any time up to the last prisoner takes his place?
During making raws...some of them can be..back to back (in any raw)...but by reaching the last prisoner,they all shoud be at the same direction
But only the first two prisoners can move.
This means the seventh prisoner, say can come into a row back to back with someone else in that row, then at a later time switch his direction so that at the end all in that row have the same direction. So as long as a prisoner stays in the same position, he can flip his direction back and forth during the formation of rows.
That sounds like communication.
Another piece of jello fell off the nail...

Yes....in my OP I said....each prisoner should choose his raw and once he did,he is not allowed to change his mind,but turning around himself was not mentioned
This seems to imply that turning around (spinning or rotating) is allowed, even though switching rows isn't allowed. Isn't that a contradiction of the requirement of the OP, which I list below
An unknown number of prisoners( more than 14)were told a day before their execution, that they are going to be blind folded, and a colored paper(either.. yellow,green,red or blue) will be glued on forehead of each one of them( no one can see his own paper), then they should inter a big hall one by one to make 4 raws in this order( Yellow,Green,Red,Blue)i.e. a raw of Yallows, a raw of Greens etc.,each one will be unfolded when he inters the hall.No one of them is allowed to arrenge the others,each one should himslf choose where to stay, once he did,he can not change his place( only the first 2 prisoners can change their minds only once). Any kind of comunication between them is not allowed. If any one of them stands in a wrong raw, all of them will die!
All colores were used.
They should make a plane which saves all of them, can you help them?
Communication is defined as 'the imparting or exchanging of information or news', so by any reasonable interpretation, turning-in-place is considered a violation of the rules. If communication is allowed, then the puzzle becomes trivial. In fact, we don't even need to allow the first 2 prisoners to change their minds if we allow them to communicate.
-
Prime, your "disproof" notwithstanding, we should congratulate you on your insight that has identified the limit towards which any experiment to 137 should tend (IMH and Naive Opinion). I'm interested to understand about Bushindo's recursive code. My contribution was only to respond to Bushindo's numeric result, as it matches the cyclic stream of digits I learned in childhood.
Here is the recursive code I used. The logic behind it is already described by Prime's excellent and insightful analysis.
Let P(N) be the probability that the total sum would eventually fall on number N. This code sets P(0) = 1, P( N ) = 0 for negative N, and then iterates recursively using a known formula as described in the following code
function P( N ) { if( N == 0 ) { return( 1 ) } else if( N < 0 ) { return( 0 ) } else { A = 1/6*( P( N - 1 ) + P( N - 2 ) + P( N - 3 ) + P( N - 4 ) + P( N - 5 ) + P( N - 6 ) ) return( A ) } } -
If I repeatedly throw a fair 6-sided die, what is the probability that the running total will at one point equal 137?
With some recursive code, I get
0.2857143
-
 1
1
-
-
-
Here's an approach,
The general strategy to determine a number N beforehand. During the game, the statistician should to look at the first N girls' cards and note the maximum dowry value among the N cards. We shall denote this maximum dowry value as M.
Having done this, the statistician should then look at the remaining (100-N) girls, and choose the first girl that has a dowry value larger than M.
The probability of winning using this strategy is
(100 - N)*N/[ 100 * 99]
Using derivatives, it is straightforward to see that the optimal choice for N is 50. So the optimal winning chance is (1/2)*(50/99)
Forgot about some cases in computation of winning chance. Back to the drawing board.
-
 1
1
-
-
Here's an approach,
The general strategy to determine a number N beforehand. During the game, the statistician should to look at the first N girls' cards and note the maximum dowry value among the N cards. We shall denote this maximum dowry value as M.
Having done this, the statistician should then look at the remaining (100-N) girls, and choose the first girl that has a dowry value larger than M.
The probability of winning using this strategy is
(100 - N)*N/[ 100 * 99]
Using derivatives, it is straightforward to see that the optimal choice for N is 50. So the optimal winning chance is (1/2)*(50/99) -
The problem is skillfully analyzed and solved by k-man and bonanova. Kudos, everyone.
Was it meant specifically for those people who are familiar with Monty Hall puzzle?
Yes, the Monty Hall reference was meant as a red herring, but apparently that false clue isn't enough around these parts.
-
Here's a twist on the Monty Hall problem.
Some of you might be familiar with a show called Deal or No Deal. For those you are not familiar, a simplified version of the show is as follows,
* There is a host, a player, and 40 suitcases of money.
* The host informs the player that there are 39 empty suitcases and 1 case with 1 million dollars. The suitcases are closed and the player has no idea how much each specific suitcase contains. At the beginning of the game, the player is requested to choose 1 suitcase at random. Let's call this the Chosen Suitcase
* At the beginning of each turn, the player is requested to choose 1 suitcase from the remaining Non-Chosen Suitcases, reveal the contents, and put this case and contents in a discarded pile. After this, the player has the choice of quitting the game and keep the content of his unopened Chosen suitcase, or switching his Chosen Case for one of the remaining Non-Chosen Cases and play on.
Let's say that the player goes through 38 turns, opening and discarding suitcases without ever switching his original Chosen Case. The 38 opened cases are all empty. There are now only 2 unopened cases left, and 1 of them is currently chosen by the player. Should he switch his original Chosen Case for the remaining Suitcase for the best chance to win 1 million dollars? Assuming optimal strategy, what is the player's probability of winning the 1 million dollars in this situation?


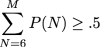
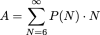

Stamps and foreheads
in New Logic/Math Puzzles
Posted
There are many cases on purpose. The reasoning should be straight forward with the proper tools and elimination procedure.