Let's say that you and 19 other prisoners are on a death row. The warden gives you and your fellow prisoners a chance to win your freedom through a game. The game is as follows,

1) When the game starts, the warden will blindfold all 20 prisoners and arrange them in a circle.

2) The warden will put on each prisoner's head either a RED or a BLACK hat. The warden will choose the color for each prisoner by flipping a fair coin.

3) The warden will then remove the blindfolds. Every prisoner will be able to see the hats on the other 19. Each person will not know the color of his own hat. There are clocks on each side of the room, so every prisoner will be able to see a clock as well.

4) The warden then says, "Everybody should be able to see the hat color of his fellow prisoners. See those clocks? For the next 20 minutes, each person may at any time raise his hand and simultaneously shout out his hat color. At the end of the 20 minutes, if everybody correctly shouted their hat colors, then you all win your freedom. Each person can only shout out his hat color once. If 1 or more person incorrectly shouted his hat color, or if 1 or more person failed to make a guess, then you all go back on the death row."

5) Each person is not allowed to communicate to his fellow prisoners during the game by varying his tone of voice, volume, facial expressions, body language, etc. The warden reserves the right to cancel the game and put everybody back on the death row if he see these types of behavior.

You and your 19 friends have 1 night to discuss a strategy. Find a strategy that makes your chances of freedom as high as possible.

[Quick Draw Aces]

Thanks for the compliment bushindo. Nice solve. And phillip 1882, as well. My approach was really quite simple. Not requiring any derivatives and pretty neat I think. Wondering some on how bushindo went about it. As for DeeGee's extension, have one idea as to where he may be going but not sure how specific of an implementation strategy he may have in mind. Will ponder further on that.

This is what I did

Let x be the probability that we draw a Red card at every turn, and let (1-x) be the probability that we draw a Black card. Let y_R( x ) be a function of our expected winning given x and given that Coop plays a Red card. Let y_B( x ) be our expected winning function if Coop plays a Black card. The explicit forms for the functions are

y_R( x ) = -2 * x + 5 * (1-x)

y_B( x ) = 5*x - 10( 1- x )

To find the optimal probability x, simply solve the equation -2 * x + 5 * (1-x) = 5*x - 10( 1- x ).

[Quick Draw Aces]

At this weeks friendly game I thought I'd try to get back a little of my money that was still in Coop's chip stack. Here was my proposed set-up: "I'll give you one red and one black ace and I'll take the other two aces. We'll both simultaneously show one ace of our chosing. If both shown aces are black, I'll give you $10; if the two shown aces are different, you pay me $5; and if both shown aces are red, I'll give you $1. Rob, our most philosophical member (read that least mathematical) asked simply, Why?" Coop now had to chime in, "You see there are four possible combinations, black-black, black-red, red-black, and red-red. So 25% of the time I should win $10, 50% of the time I lose $5, and 25% of the time I should win $1. Out of four games then, I should win $1 on average." I liked the way Coop was already speaking in the first person; it was time to reel him in. "Okay Coop, I'll make that $2 I'll pay out for every red-red combination." Coop couldn't resist at this point, "You're on but I get to decide when we quit. Huck can keep the tally." Vern just chuckled in amusement. I gave Coop the two pointed aces and the game was on. At least three times I asked Coop in a worried tone if he had had enough but not until we must have played 300 hands or more did he ask Huck what the tally was. When Huck told him he was down $72 Coop exclaimed, "You're drunk!" Though that very usually is the case, the results were accurate. "Damn, stop me at $100." Shortly thereafter, Coop handed me what I hoped was the same $100 bill he flashed last week as enticement into his little prop bet. Was I just lucky? If not, what was my strategy?

This is a really nice puzzle.

At every game, choose Red with probability 15/22, and choose black with probability 7/22. You have an expected wining of 5/22 dollar/hand regardless of what Coop does.

Choose a and b randomly, uniformly [0,1].

We're going to break a unit stick in two places, a, and b.

c = min(a,b)

d=max(a,b)

x=c

y=d-c

z=1-d

Brilliant and elegant solution, CaptainEd. It also has the bonus of generalizing easily to higher dimensions. I'm in awe.

I mean #2. I'm sorry that I wasn't clear about that.

Here's a method for generalizing the solution to the OP to any arbitrary number of dimension

Let R( a, b ) be a random generator function that returns a uniform random number between a and b. We want to generate random vectors (x₁, ..., x_n ) such that x₁ + ... + x_n = 1, and 0 < x_i < 1. Let's call this desired high dimensional region U. The outline of this solution is that we will generate vectors within U non-uniformly. However, we will compute for each generated vector a rescaling weight and will take it back to the uniform distribution. The method is as follows

1) We first compute a single vector (x₁, ..., x_n ) within U. The first (n-1) elements will require the random number generator R( ). The computation of the elements of this vector goes as follows

x₁ = R( 0, 1 ) // the first element is a random number between 0 and 1

x₂ = R( 0, 1 - x₁ ) // the second element is a random number between 0 and (1- x₁ )

...

x_n-1 = R( 0, 1 - x₁ - x₂ ... - x_n-2 )

x_n = 1 - x₁ - x₂ - ... - x_n-1

The vector generated above is guaranteed to be inside the region U. However, it is by no means considered to be a uniformly random vector within U. Fortunately, we can compute the rescaling weights to convert it to a uniform distribution.

2) For the vector described in 1), we compute the corresponding rescaling weight, w. Let

w₁ = 1

w₂ = 1 - x₁

...

w_n-1 = 1 - x₁ - x₂ ... - x_n-2

Finally, the rescaling weight is

w = w₁ * w₂ * ... w_n-1

3) Repeat step 1) and 2) for M times to obtain M vectors and M corresponding rescaling weight. Call this set of M generated vectors V. Call the set of rescalling weights W.

4) To generate a vector uniformly within U, we sample a single vector from the set V using the weights W. That is, the vectors with higher weights have higher chance of being selected, and vectors with low weights have lower chance of being selected. Repeat this step as necessary to get more uniformly distributed vectors in U

Here's a discussion of why the 15 people won't all abstain during the same turn.

So, let's index the 15 people from with numbers from 1 to 15. Let the hat color be represented by 1's and 0's. In the hamming code solution, we essentially assume that 11 people are the 'data' (encoded by d_i in the following table), and the other 4 people are the 'error checking bits' (encoded by p_i).

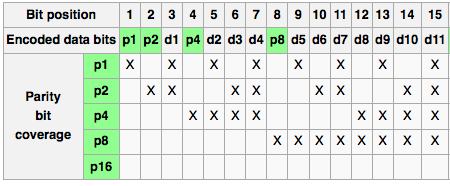
So, according to the chart above, we are assuming that in modulo 2 arithmetics,

p_1 = d_1 + d_2 + d_4 + d_5 + d_7 + d9 + d_11

p_2 = d_1 + d_3 + d_4 + d_5 + d_7 + d_10 + d_11

...

p_8 = ..

So, the 15 people in the game are assuming that p_1, p_2, p_4, and p_8 follow the 4 equations above. Let's enumerate the cases, and show that none of those cases result in everyone abstaining

a) p_1 to p_8 follow the hamming encoding equation (the probability of this happening is 1/16). Following the rules of the solution, all 15 would successfully solve for their hat color assuming that the hamming encoding rules are true. All 15 would then simultaneously guess the opposite color. Everybody lose.

b) one of the 4 error checking people (p_i) has the opposite bit of what the hamming encoding rule says. p_i would then be able to calculate his hat color from the rules, and the guess the opposite of it. Everybody else would abstain because they would realize the encoding assumption doesn't apply. Everybody win.

c) two of the 4 error people (p_i and p_j) have the opposite bit of what the encoding rule says. Looking at the data table, there is a data person (d_i) whose column includes precisely the two people with error. This data person would then be able to calculate this hat and guess the opposite of it. For instance, let's say that p_1 and p_2 have the opposite bits of the encoding rules. The data person d_1 would then be able to correctly guess his hat color. Everybody win

d) 3 of the 4 error people have the opposite bit of what the encoding rule says. Looking at the data table, there is a data person (d_i) whose column includes precisely the three people with error. For instance, let's say that p_1, p_2, and p_4 dont follow the encoding rules. Then the data person d_4 would raise his hand and guess correctly. Everybody win

e) Let's say all 4 error checking people's hats don't follow the encoding rule. The data person d_11 would then correctly guess his hat color. Everybody win

Note that there are 6 data people that each covers two error checking people (d_1, d_2, d_3, d_5, etc. ). There are 4 data people that each covers three error checking people, and 1 data person (d_11) that covers all four. It is no accident that these numbers are precisely ₄C₂, ₄C₃, and ₄C₁, and they add together to form 11.

Minor correction to the last paragraph in the spoiler.

Note that there are 6 data people that each covers two error checking people (d_1, d_2, d_3, d_5, etc. ). There are 4 data people that each covers three error checking people, and 1 data person (d_11) that covers all four. It is no accident that these numbers are precisely ₄C₂, ₄C₃, and ₄C₄, and they add together to form 11.

My take on araver's discussion is that earlier solutions did not adequately rule out cases where everyone would abstain.

That point, I could not see had been covered.

In my that point was clear, because the 8 cases could easily be enumerated.

Here's a discussion of why the 15 people won't all abstain during the same turn.

So, let's index the 15 people from with numbers from 1 to 15. Let the hat color be represented by 1's and 0's. In the hamming code solution, we essentially assume that 11 people are the 'data' (encoded by d_i in the following table), and the other 4 people are the 'error checking bits' (encoded by p_i).

So, according to the chart above, we are assuming that in modulo 2 arithmetics,

p_1 = d_1 + d_2 + d_4 + d_5 + d_7 + d9 + d_11

p_2 = d_1 + d_3 + d_4 + d_5 + d_7 + d_10 + d_11

...

p_8 = ..

So, the 15 people in the game are assuming that p_1, p_2, p_4, and p_8 follow the 4 equations above. Let's enumerate the cases, and show that none of those cases result in everyone abstaining

a) p_1 to p_8 follow the hamming encoding equation (the probability of this happening is 1/16). Following the rules of the solution, all 15 would successfully solve for their hat color assuming that the hamming encoding rules are true. All 15 would then simultaneously guess the opposite color. Everybody lose.

b) one of the 4 error checking people (p_i) has the opposite bit of what the hamming encoding rule says. p_i would then be able to calculate his hat color from the rules, and the guess the opposite of it. Everybody else would abstain because they would realize the encoding assumption doesn't apply. Everybody win.

c) two of the 4 error people (p_i and p_j) have the opposite bit of what the encoding rule says. Looking at the data table, there is a data person (d_i) whose column includes precisely the two people with error. This data person would then be able to calculate this hat and guess the opposite of it. For instance, let's say that p_1 and p_2 have the opposite bits of the encoding rules. The data person d_1 would then be able to correctly guess his hat color. Everybody win

d) 3 of the 4 error people have the opposite bit of what the encoding rule says. Looking at the data table, there is a data person (d_i) whose column includes precisely the three people with error. For instance, let's say that p_1, p_2, and p_4 dont follow the encoding rules. Then the data person d_4 would raise his hand and guess correctly. Everybody win

e) Let's say all 4 error checking people's hats don't follow the encoding rule. The data person d_11 would then correctly guess his hat color. Everybody win

Note that there are 6 data people that each covers two error checking people (d_1, d_2, d_3, d_5, etc. ). There are 4 data people that each covers three error checking people, and 1 data person (d_11) that covers all four. It is no accident that these numbers are precisely ₄C₂, ₄C₃, and ₄C₁, and they add together to form 11.

Here's an alternative method to solve the 3-D problem in the OP. Unlike plasmid's elegant solution, this one uses conditional translation and rotation.

Let a and b are numbers uniformly generated between 0 and 1. We can randomly generate numbers (x, y, z) from the region determined by x+y+z = 1, 0<x<1, 0<y<1, 0<z<1 using the following formula

x = floor( a + b )*( -b + 1) + (1 - floor( a + b ))*( a)

y = floor( a + b )*( -a + 1) + (1 - floor( a + b ))*( b)

z = 1 - x - y

I put this problem up because someone told me a simple method of uniformly generating discrete distributions of any dimension.

At the time, I was concerned so much about filling my immediate need for such a thing, that I didn't bother asking for a

proof of the method. I had hoped that someone on the Den might know of it. I was very happy that you guys did such a nice

job analyzing the problem and coming up with the solutions that you did. But, so far, nobody has come up with the method I

was given years back. If nobody comes up with it within a few days, I'll post it and ask if anyone can prove/disprove

that it works.

Thanks!

I would like some clarification. When you say 'generalize to higher dimensional space', do you mean

1) Given a random number generator that uniformly produce numbers between 0 and 1 and a description of ANY high dimensional region (e.g., a sphere in 3D, a circle in 2D, a triangle in a plane embedded within 3D space as described in the OP, etc.), produce a method that uniformly sample coordinates within the described high dimensional region.

or

2) Given a random number generator that uniformly produce numbers between 0 and 1, uniformly sample the vector (x₁, ...,x_n ), where x₁ + x₂ + ... + x_n = 1 and 0< x_i < 1 for i = 1, 2, ..., n?

It is possible to uniformly generate numbers in a 3-dimensional region from a single draw of a random number generator without discretizing the 3-d volume into small, finite regions.

Let's assume that we have a random number generator that generates number between 0 and 1. The procedure is as below

1) Generate the single number from the generator between 0 and 1. Call this number a

2) Contruct the first number by taking (counting from the right of the decimal point) only the 1st, 4th, 7th, 10th, and so on digits of a. Put a decimal in front of this number newly constructed number

3) Construct the second number from the 2nd, 5th, 8th, 11th, and so on of a. Construct the third number using the 3th, 6th, 9th, 12th, and so on digit of a.

Example:

Let's say that we randomly generate a as

.274648369361...

We would then construct the first number using digits 2, 6, 3, 3, and all other digits at the (1 + 3*i) positions, where i = 0, 1, 2, ....

First number = .2633...

The second number would be constructed from the (2 + 3*i) positions, where i = 0, 1, 2, 3, ...

Second number = .7466...

By the same procedure, the third number is

.4891...

If the original number is uniform on [0,1], then the 3 numbers just generated are each uniform on [0,1] as well. We can easily extend this methodology to any arbitrary number of dimensions from a single random number.

I apologize for posting a solution that is the same as plasmid. I read the spoiler title which said that the method is 'kludgey', and assumed that interleaving digits on numbers with infinite digits isn't kludgey, so his solution can't be the one I was thinking of. You know what people say about decomposing the word 'assume'. I feel that way right now.

Did you have a different method in mind to convert a single random number into a three dimensional coordinate with uniform probability density? Aside from CaptainEd's geometrical method, I'm having a hard time finding a way of doing it elegantly.

It is possible to uniformly generate numbers in a 3-dimensional region from a single draw of a random number generator without discretizing the 3-d volume into small, finite regions.

Let's assume that we have a random number generator that generates number between 0 and 1. The procedure is as below

1) Generate the single number from the generator between 0 and 1. Call this number a

2) Contruct the first number by taking (counting from the right of the decimal point) only the 1st, 4th, 7th, 10th, and so on digits of a. Put a decimal in front of this number newly constructed number

3) Construct the second number from the 2nd, 5th, 8th, 11th, and so on of a. Construct the third number using the 3th, 6th, 9th, 12th, and so on digit of a.

Example:

Let's say that we randomly generate a as

.274648369361...

We would then construct the first number using digits 2, 6, 3, 3, and all other digits at the (1 + 3*i) positions, where i = 0, 1, 2, ....

First number = .2633...

The second number would be constructed from the (2 + 3*i) positions, where i = 0, 1, 2, 3, ...

Second number = .7466...

By the same procedure, the third number is

.4891...

If the original number is uniform on [0,1], then the 3 numbers just generated are each uniform on [0,1] as well. We can easily extend this methodology to any arbitrary number of dimensions from a single random number.

Suppose you see before you 10 identical-looking

blocks. No two of these blocks weigh the same.

Your task is to sort the blocks according to

weight using the fewest number of weighings.

You get to chose which scale you would like to

use for all the weighings. The scales are

labeled S2, S3, S4, S5, S6, S7, S8, and S9.

Once you choose a scale, you must use it

exclusively. If you choose scale SN (where

N is between 2 and 9 inclusive), then it will

only weigh a subset containing precisely N

blocks. The scale will then sort the N blocks

according to weight and report this weight-

ordering to you. What value of N will allow

you to determine the weight-ordering of all

10 blocks in the fewest number of weighings?

Maybe i'm missing something somewhere...

S9 will result in the fewest weighings. Notice that S9 can duplicate the functionality of any SN, where N<9. For instance, suppose we want to use S9 to weigh 7 objects. Simply put the 7 desired objects on S9 along with 2 other objects (let's call them placeholders), and then discard the rank of the 2 placeholders in the final ranking.

So, if S_i for some i < 9 results in the fewest number of weighings, then S9 can duplicate the function of S_i and hence possesses that property too.

You're right. I found a bug in my program (it's been a while since I wrote anything myself) where it was verifying the results. Now I see that there are 123 sets of answers that produce multiple arrangements with no way to identify a truth teller.

Bushindo, is this the same answer you had in mind?

Apparently you and I both had bugs in our codes. My bug has no other explanation besides a sloppiness on my part. Mea culpa.

What about the answer sequence YNYYNYNNNN?

There are 10 arrangements (T=Truth Teller, R=Random Speaker) which give this answer:

TTRTTRTRTRR

TTRTTRTRRTR

TTRTTRRTRTR

TTRTTRTRRRT

TTRTTRRTRRT

TTRTTRRRTRT

RTRTTRTRTRT

TTRRTRTRTRT

RRTTTRTRTRT

TTRRRTTRTRT

So, a Truth Teller cannot be identified here.

Am I missing something?

This board never fails to amaze me. Good work, superprismatic.

I wrote a little program to validate my solution and it works in all 1024 possible combinations of Yes/No answers. Amazingly enough, every combination of Yes/No answers produces at least one valid arrangement of people. And, in cases when multiple arrangements are possible, there is always at least one Truth Teller that can be identified.

Great work, k-man. The exhaustive proof is a very nice bonus. This board never fails to amaze me =)

I ask person A the following question:

"If I were to ask you whether Person B is a 'Truthteller', would you say Yes?"

If A is a TT and B is a TT: Answer Yes

If A is a RS and B is a TT: Answer Yes

If A is a TT and B is a RS: Answer No

If A is a RS and B is a RS: Answer No

So, is the answer is Yes, you choose B.

If you are unlucky, you may have to repeat this for maximum six times to get your man.

Ah, I see I was sloppy in phrasing this problem. By random speakers, I mean that these people randomly answer Yes or No to any question. That should bring the puzzle back along the intended line.

You are an explorer traveling in the Amazon rain forest. You need to explore a particularly dangerous region of the forest, so you drop by a local village of Tourguidians to hire a native as an expedition guide. The Tourguidians are the best guides to the Amazon forest. However, they are divided into 2 sub-groups: the truth tellers and the random speakers. The truth tellers will always respond to questions with the truth, while the random speakers will randomly tell the truth or lie to any question.

There are 11 Tourguidians in this particular village, 6 of whom are truth tellers, and 5 are random speakers. You don't know which person belongs to which group. You would like to find a truth teller and hire him for obvious reasons ("Umm, is this herb poisonous, Mr. Tour Guide?"). However, you are only allowed to address a total of 10 questions to the villagers. Each question may be addressed to any 1 of the 11 villagers. The restrictions are that they be Yes/No questions, and that you can not ask any question which is impossible for a truth teller to answer with a yes/no (ie. asking a truth teller what a random answerer would say to a particular question, asking paradoxes, etc. )

Devise a strategy that is guaranteed to identify a truth teller in the 11 villagers using only 10 questions. Assume that each villager know the identity/persona of his fellow villagers.

my apologies, it's supposed to be WINSCONSIN.

This is a joke, right?

How can you measure the thickness of an ordinary A4 piece of paper with tools available in the average household?

I just tested this new strategy. It works very well. Again, a generous interpretation of 'tools in the average household' is required.

Take out your wallet. Remove a 5 dollar bill. Locate a niece/nephew and say 'Dear niece/nephew, I will give you this 5 dollar bill if you can tell me what is the thickness of an A4 piece of paper using the tools in the average household." Watch in amusement as niece/nephew scamper away to work on the problem.

If your household does not have any niece/nephew, free free to replace them with spouses, children, grandparents, neighbors, etc.

If you have more than one niece/nephew, you may remain impartial, and at the same time foster a healthy spirit of competition, by saying "I will give this 5 dollar bill to the first person who correctly tells me the thickness of an A4 piece of paper using the tools in the average household.".

I'm definitely in over my head from a math theory perspective, I just found the answer to be interesting from a logic perspective. Clearly, the answer approaches 50%, but I also think it approaches from the high side, which is all the puzzles was looking for.You definitely wouldn't be looking to make any large bets at even money.

I was talking to another friend about this puzzle and he preferred to think about a uniform function that produces numbers from 0,1, where each number is as likely as any other. So two questions.

1. Let's say that you know the function and after I use the function to produce two numbers, you use the function to produce one number. You then look at the first of my two numbers and switch if it's smaller than your number and stay if it's bigger. What are your odds of ending up with the bigger of my two numbers?

2. Since you know that the function produces a smooth distribution from 0,1, you use the optimal strategy, which is to stay with the first number is it's larger than .5 and switch if it's smaller. If you use that strategy, what are your odds of ending up with the larger number?

Some comments

Clearly, the answer is approaching 50%. But from the mathematical perspective, this is indistinguishable from 50 itself. For instance, if you try to capture the performance in a finite number, say 50.000.....0001% as in the OP where I assume there is a fixed but unknown number of 0's represented by the dots, we can easily prove that the performance is smaller than that fixed number.

An analogy to this curious behavior is the set of rational numbers and irrational numbers. Let's say we look at the interval [0,1] and sample uniformly from it. What is our chance of sampling a rational number? Obviously it is larger than 0. However, because the set of irrational numbers is infinitely larger than the set of rational numbers, our probability of sampling a rational number is approaching 0 from the positive side, so we essentially treat that probability as 0.

Back to the instance where your friend preferred to think of the prior distribution as the uniform distribution on [0,1]. Notice that this changes the whole problem dramatically. Essentially, your friend is adding prior information to the problem, and this prior information can be used to achieve performance better than 50%. In the original problem, the only information we know is 1 of the 2 numbers, and that the generating function p(x) could be ANY function. The fact that I have no idea what this function p(x) is an integral part of the original problem.

In this modified problem, we know 1 of the 2 numbers, and the generating function p(x) = Uniform( 0, 1) itself. The latter is extra information because now, for instance, we immediately know if our number is above or below the median of p(x). Let's say that the two generated numbers are A and B, and we chose A. Given the prior information, we immediately known the probability that B < A, and probability B > A. We couldn't do that with the original problem. The extra performance then, shouldn't be a surprise.

So, back to your questions, lets assume p(x) = Uniform( 0, 1)

1) Let's say we sample A and B as our two numbers, and C as a third number. Let A be the number that is revealed. We arrange the numbers in increasing order, there are 6 possibilities that are equally likely:

A,B,C

A,C,B

B,A,C

B,C,A

C,A,B,

C,B,A

It's easy to see that we would win 2/3 of the time if we generate C uniformly from [0, 1].

2) Let's say we sample A and B as our two numbers, and C as a third number is equal to .5. Then, our strategy would win if min( A, B) < .5 < max( A, B). That is, our strategy would win 100% of the time if .5 is between A and B, and 50% otherwise. The chance that min( A, B) < .5 < max( A, B) is 1/2, so the expected performance is

1/2 * (100%) + 1/2 * (50%) = 75%.

First, add in two beakers of water (simpler explanation)

Second, kill one rat for fun. Mwaahaha. Or let it go (added in case PETA is watching...).

Third, since 32 is 2^5, do 5 tests of mixing 16 beakers. This will be done in the regular binary fashion. One possibility listed below:

Test 1: Odds

Test 2: 1-2,5-6,9-10,13-14,17-18,21-22,25-26,29-30

Test 3: 1-4,9-12,17-20,25-28

Test 4: 1-8,17-24

Test 5: 1-16

(Notice that at least 1 test must end up with a dead rat (i.e., you cannot have both poisons in each of the tests that has any poison, and only 1 beaker is left untested (32)).)

Fourth, choose one of the tests that killed a rat, and do a binary search through it for the poison. This will take 4 tests since 2^4 is 16 and the original test had 16 mixed beakers.

Fifth.... oh no! no more rats to test! That's ok, we know where one of the beakers of poison is, so toggle the results from the first 5 tests that contain the poison we know of, and it will give you the location to the other beaker of poison.

Example:

Test 1: dead = 1

Test 2: live = 0

Test 3: live = 0

Test 4: dead = 1

Test 5: dead = 1

We found the poison in beaker 17 (just chosen arbitrarily). 17 was used in tests 1-4, so toggling those tests results in:

Test 1: toggled = 0

Test 2: toggled = 1

Test 3: toggled = 1

Test 4: toggled = 0

Test 5: dead = 1

So, what number was in test {2,3,5} and not in {1,4}? 10!

So the poisons were in beakers 17 and 10.

If I would have set up the tests differently, it would have been simpler to find the last beaker (adding powers of two), but I'll leave that as an exercise to the reader.(i.e., me == lazy)

Though I will give a (lazy) proof of the claim that at least 1 test will kill a rat.

Since the position of the poison is essentially a set of the tests that get toggled due to it being poisoned, having two poisoned beakers and all tests with live rats means that the two binary positions (set of tests resulting in dead rats) of the two poisoned beakers would need to be identical since they toggled the exact same tests. Since that cannot be, and we know there are 2 unique ones, there must be at least 1 test of the first 5 resulting in a dead rat.

Edit:: Perhaps the extra rat could be a check at the end to make sure the warden isn't trying to trick you by having 3 or 1 poisoned beaker. Those evil wardens...

Anyone see a mistake?

Good work, EventHorizon. Nice job going beyond the call of duty. As a prize, you get both your freedom, and the 10th rat for a pet .

Suppose that you are a prisoner on the death row. The warden offers you a chance for freedom through a game.

The game is as follows:

1) The warden shows you an array of 30 identical beakers, each containing an identical amount of clear fluid.

2) You are told that 28 beakers contain simply water. 2 beakers (you don't know which ones) contain deathly poisons which can render death in exactly 1 minute.

3) You are offered 10 live rats and 10 empty flasks. You can take turn testing for poison using the rats.

4) At each turn, you must mix fluids from any number of the 30 beakers into one of the flasks. Once done, you can feed that mixture to a rat, wait 1 min, and see if it dies or not. Only 10 turns are allowed (you can not reuse flasks or rats).

5) Assume that the poisons are sufficiently powerful that even the most minuscule amount in a mixture is sufficient to kill a rat in exactly 1 minute. Also, the poisons are very odd in that while each of them is very deathly alone, mixing them together (in any proportion) in the same flask will render the mixture completely harmless.

The goal is to identify the 2 beakers containing the poison at the end of 10 turns. If you are correct, you will be set free. If not, you'll be forced to drink 10 random beakers from the 30 =).

Find a strategy that is guaranteed to correctly identify the 2 poisoned beakers.

measure the thickness of a stack of 1000 papers or more, then divide whatever u got by the number of paper used.. the larger the stack the more accurate the result.

but since counting 1000 papers is daunting, weigh 100 papers and divide by 100 to get the weight of a single paper (the result here has less error than measuring the length of a stack of 100 papers, assuming u used an accurate enough scale), then get a VERY large stack of A4 papers, weigh them, divide by the weight of a single paper to get the number of papers, say n.. then measure the thickness of the big stack and divide by n.

For a generous interpretation of 'tools in the average household'

Turn on the computer. Go to google and type 'thickness of A4 of paper'.

Alternatively, go to the phone and call 411. Or simply call any printing shop and ask.

If we don't have a large supply of paper, one way is to cut the paper into thin rectangular strip. Roll the strip into a cylindrical roll like the following image (except that you'll have no hole in the center). Measure the radius of the roll and you can easily solve for the thickness.

@Bushindo

I agree with everything you said. The only thing I'm not sure about is why you are talking about distributions within limited intervals. The OP states that the function produces the numbers in the range (-inf,+inf). Of course, all the subintervals will fit that description, but I assumed that any real number can be picked even though the distribution is not given.

The solution of fixing at Zero doesn't work for ALL generating functions, but works for those that are capable of producing one positive and one negative number in the pair.

Please note that there is no requirement that p(x) be a distribution with limited support (finite domain). The examples of the uniform distribution and binomial distribution that I gave have finite domain, but the gaussian example has unbounded support (-infinity to infinity). The gaussian distribution can potentially generate any number from -infinity to infinity, though certain numbers tend to show up more often. This is just as well, because while the OP states that any number from -infinity to infinity may be generated by this mysterious density distribution, it doesn't say that all numbers are equally likely to show up. In fact, we would run into trouble if the OP requires that all numbers between -infinity and infinity be equally likely. Here is a discussion on why sampling uniformly from the infinite number line is not possible (text).

In post #9, I used uniform sampling on the infinite number line to show that this methodology will not improve beyond 50%. Further research into the topic has shown that uniform sampling on the infinite line is not possible, as it may lead to some logical contradiction. Please ignore post #9.

The fact that the OP is can successfully generate two numbers from the unknown distribution p(x) implies that this distribution is a well-defined probability distribution. And thus well-definedness is the only requirement we impose on p(x).

I actually like the approach with zero better. It's the same idea, but it doesn't require you picking a random number every time, but rather fixing it at zero. Essentially, we don't know anything about the function you're using to pick 2 numbers, but if the function always yields 2 positive or 2 negative numbers then you have exactly 50/50 chance of winning. If the function ever gives one positive and one negative number, then your odds just shifted to something more favorable than 50/50.

Some comment on this approach

Let's clarify things first, and let's p(x) be the distribution from which we are drawing the two initial numbers. p(x) can be ANY distribution, e.g., a gaussian distribution centered at -1 with standard deviation 1, a uniform distribution on [10, 20], or a binomial distribution with outcomes 100 and 101, etc.

The approach where we select 0 and then apply the methodology will work the best if our p(x) is symmetric around 0. For example, it works the best if our distribution function is gaussian centered at 0 with some standard deviation, or if p(x) is uniformly distributed on [-2, 2]. This is because then we are equally likely to select a positive number as to select a negative number. It is easy to see then that the methodology doesn't do much better than random guessing if our distribution function is asymmetric with respect to 0, e.g. p(x) is uniformly distributed on [1, 10], or p(x) is gaussian with center 10 and standard deviation 1.

To simplify things, lets say that if p(x) if symmetric to 0, then our methodology will do better than 50%, and if p(x) is sufficiently asymmetric, then the methodology is only as good as 50%. To calculate the performance of the methodology, we will need to consider the relative 'size' of the two classes. My claim is that the asymmetric class is infinitely larger than the symmetric class, so the expected performance of the methodology is approaching 50%.

Now, imagine that for every distribution function p(x) that is symmetric, we can easily shift the entire distribution left or right by a distance R and get a distribution that is asymmetric. That is, if p(x) is symmetric, then we can simply make up a real number R, and then p( x - R ) is asymmetric. There are an infinite number of such R, so there are an infinite number of asymmetric shifted distribution for every symmetric p(x).

For example, let's consider the symmetric uniform distribution on [-1, 1]. This p(x) has performance that is better than 50%. However, we can keep shifting the entire interval by 1 to the right, and get an asymmetric uniformly distributed interval each time. For instance, the intervals [0, 2], [1, 3], [2, 4], [3, 5], [4, 6], ... will each have performance = 50%. Repeat ad infinitum.

Note that this argument assumes that in the OP, the two numbers are generated independently from the same univariate p(x). If the two numbers are jointly generated via a bivariate distribution function, then we can simply extend the argument above to 2-dimension and it will work exactly the same.

Create a function that will produce a single number, for simplicity, it can be normally distributed across all real numbers. Generate a number. Then look at one of my numbers. If the your number is lower, stick with the first number you looked at. If your number is higher, then switch.

Here is the reasoning why that makes you slightly better than 50-50. Let's assume that the two numbers I picked are 1,000 and 2,000. If you use this strategy, you will win 100% of the time you generate a number in between 1,000 and 2,000. While, if you generate a number higher or lower, you will be exactly 50-50. For example, if your number is 10,000, then you win if you look at 1,000 first, and if your number is 0, you win if you look at 2,000 first. So, you can simply argue, that given any two of my numbers, you are exactly 50-50, unless you pick a number in between my two numbers, in which case you are 100%. Therefore you must be better than 50-50.

I can't think of a way to refute the logic.

I think the fact that we can not produce a single percentage for the performance of this strategy is telling. It may be suggesting that the performance is approaching 50% from above, similar to how .9999999.... is approaching 1 from below.

It seems to be that this strategy is somewhat equivalent to saying that if we randomly generate 2 numbers between -∞ to ∞, then the two numbers, call them a and b, will divide the number line into (-∞, a), [a, b], and (b, ∞). We then generate a number C, and then our strategy is 100% if C is in [a, b], and 50% if C is not in [a, b]. However, the fact that we are dealing with the infinite line makes this problem less straight forward than it seems.

Let's simplify things for a moment and say that we sample C from A to B, where A < a, and B > b. Then the chance that C falls within [a, b] is equal to (b -a )/(B - A). However, if we let A -> -∞, and B -> ∞, it is easy to see that the chance that a randomly chosen number falling between [a,b] is approaching 0. It seems that we are then back to the 50% limit.

I will choose two real numbers using a function that will produce numbers from -infinity to +infinity. You have no idea what function I'm using. It doesn't have to normally distributed.

I will write those two numbers on two different pieces of paper. You will look at one of the numbers. You can then choose whether to stay with that number or switch. You goal is to come up with a method to end up with the higher number more often than 50%. As long as your method is 50.000000.....000001% (probably the best you can do), you have solved it. Enjoy!

Is it possible for the 2 generated number to be the same?