bushindo
-
Posts
719 -
Joined
-
Last visited
-
Days Won
5
Content Type
Profiles
Forums
Events
Gallery
Blogs
Posts posted by bushindo
-
-
Honestly, I haven't looked at enough of this kind of problem to know what the hallmarks are, but in this situation, the fishermen should be able to solve what color hat they are wearing through just logic, and not strategy, given that the fishermen figure out a way to alert all the other players when they've figured out their hat (which you did). I could ask for the algorithms for all the fisherman, but I think asking for the first fisherman's algorithm/set of rules will suffice to make people consider about all the possibilities. I put the gongs in to make it easier to mark the time and define the algorithm.
My impression of the claim you intend the BD to prove is the following:
Claim: Given that the fishermen figure out a way to alert all the other players when they've figured out their hat, then the fishermen should be able to solve what color hat they are wearing through just logic; that is, they do not need to confer among themselves for a common strategy.
In other words, let's say that we remove the fishlines from the problem, and just assume that there is a royal announcer. Every time participant X raises his hand, the royal announcer would then intone within all participant's hearing "Participant X is ready to guess his hat color". Are you saying that, without absolutely no talking among themselves before the game start, the 5 participants can logically come to a solution that is guaranteed to win?
-
An excellent strategy! Although, in the story, I was trying to convey (and I guess didn't) that they didn't have a lot of time to come up with a strategy of say "you raise your hand when to indicate a particular arrangement". But major points to Bushindo for his solution.
Also, I was trying to convey (by the rules) that they couldn't speak or look at each other until their respective gong rang, so there needed to be another element to alert them to the others raising their hands, hence the fishing line, which Bushindo correctly arranged. Looking at the final shape...well, it's befitting the most benevolent king, don't you think?
Anyways, let me ask this question then. If there was no time to devise and agree on a strategy, hence allowing the fishermen only to raise their hand when they knew their own color of hat, what is the algorithm for the first fisherman?
This is puzzling, since a previously-agreed-upon strategy is the hallmark of these everyone-must-be-correct-to-win problems. I would like some clarification. Do you mean to say "If there was no time to devise and agree on a strategy, hence allowing the fishermen only to raise their hand when they knew their own color of hat, what is the algorithm for the first fisherman such that the 5 participants are guaranteed to win?" Or perhaps you mean to ask for an algorithm for the first fisherman such that the chance of fishermen winning is as high as possible?
-
That's the other part of the puzzle
. Plasmid was very close, the answer to that part just needs to be refined to fit the specified rules laid down by his oh-so-munificent majesty. ;PWell, here's are some strategies
Suppose that whenever a participant raises his hand, the other 4 participant would be aware of this fact. Here's a general strategy that would allow all 5 participants to win.
I) After the first gong sounding, participant 1, who is the closest one to the king, is to raise his hand if he sees 2 black hats. Everyone should be able to figure their hat colors if this happens.
II) If the second gong sounds and participant 1 didn't raise his hand, then there are four classes of hat patterns, which are listed in the drawing below. (Note that the classes of patterns are listed as A, B, C, and D, each of which may include mirror images of one another along the vertical axis. For instance, in class A, the hat colors of participants 2a and 2b can be reversed without consequence on the following strategy).
III) After the second gong sounding, participants 2a and 2b are each supposed to raise his hand if he or she sees 2 hats of the same colors (2 whites or 2 blacks). Let's say that 2a raises his hand after the second gong sounds, then the hat patterns fall into class A or B. Participant 2b would then be able to figure out which pattern it is, and he needs to convey this information to participants 1, 3a, and 3b.
III-a) If the pattern is A, then participant 2b should raise his hand after participant 2a, but before the third gong sounding.
III-b) If the pattern is B, then participant 2b should raise his hand after the third gong sounding. Everyone else should be able to figure out his hat color. Participants 3a and 3b may need to observe each other's hat before being able to calculate their own color.
IV) If the third gong sounds and no one has raised his hand yet, then the hat pattern is either C or D. At this point, participants 2a and 2b would know which is the true pattern and they can convey it to the rest with the following:
IV-a) If the pattern is C, then participant 2a should raise his hand after the third gong.
IV-b) If the pattern is D, then participant 2b should raise his hand after the third gong. Everyone else should be able to figure out his color.
Minor details about the fish lines
In the general strategy, we assumed that whenever a participant raises his hand, the other 4 participant would be aware of this fact. The information in the OP doesn't specify whether this assumption is true or not.
1) If the assumption is true, things are all well and good.
2) If the assumption is not true, then simply use the fishlines to attach each participant to the other four. For instance, we could attach four lines from participant 1 to the thumbs of each of the other four, then attach four lines from participant 2a to the index finger of each of the other 4, and so on. Whenever a participant raises his hand, simply hold on to the fishlines as he or she raises the hand, and the other 4 would know who raised the hand.
-
Having grown ennuied of torturing prisoners on death row with hat problems (after all, where was the suspense if they had nothing to lose?), the sadistic king decided it was time to expand his horizons.
As luck would have it, today was the day the fishermen's guild was sending its tribute, brought by five of its most capable members. After graciously receiving a crate of fresh, lovely salmon, mahi mahi, and white tuna, the king thanked his guests by promptly ordering their arrest.
"But what did we do?" the unfortunate artisans asked.
"You are harming the kingdom. Your practices are not..." the king searched for the politically correct buzzword of the day, "...sustainable. Hence, you will be put to death."
The fishermen pleaded and begged for mercy. The king reclined in his throne, covering his smile with his generously ringed hand, and savored the moment. Finally, he raised the hand for silence.
"I am a benevolent and fair ruler," he proclaimed, "Hence, I will allow you one chance to save yourselves." He gestured to his manservant, who, all too familiar with the drill by now, went to fetch his box of hats. The king continued, "After my manservant returns, I will have you all stand, facing the directions I specify, with eyes closed, in a circle in front of me." He gestured towards the expansive floor of the throne room. "Then I will have my manservant place a hat on each of your heads. There are three white hats and two black hats. Without speaking or moving in any way other than I direct, you must determine what color the hat on top of your own head is, and when you do, you may raise your hand and my manservant will come to you and you may whisper the color in his ear."
"So if one of us figures out the color of out hat, we all go free?" asked one fisherman who had heard mention of the king's tyrannical games before.
But the king shook his head in a lordly manner. "You must ALL determine the color of the hat you each wear. If one man declares an incorrect color, you will all be executed."
"But, surely, you can't expect us to figure out the color of our hat with no information...your majesty," another fisherman protested.
"Of course not," the king stated. "I am much too beneficient." He nodded towards a large bronze gong residing in one corner. "When the gong sounds the first time, the man closest to me may look at the hats of the two standing closest to him. When the gong sounds the second time, the two men farthest from me may look at each other's hats, and the hat of the man standing closest to me. When the gong sounds the third and final time, the remaining two men may look at each other's hats. My guards will be stationed closely to prevent cheating. If cheating is attempted, you will all be executed."
The fisherman shot glances at each other. "But, your munificent majesty," one finally spoke, "we need something more, if we are not allowed to speak or move other than to look or raise our hands."
"Well, too bad," the king replied, yawning. "That's all I'm giving you."
The most diminutive and bravest of the fishermen asked, "What if we use something we already have? Then you don't have to give us anything."
The king stroked his chin. The only thing the men had on them, besides their clothes, was fishing line. He shrugged. "Sure, let's just get this party started."
The fisherman huddled together for a few moments, then positioned themselves as directed, evenly spaced in a large circle. Shortly, the manservant returned with the hats and the game was afoot.
What is the maximum number of the fisherman that can raise their hand after the second gong but before the third gong?
How will the fisherman standing closest to the king determine what color his hat is?
I would like some clarification. My impression is that whenever a participant raises his hand, the other 4 participant would be aware of this fact. For instance, if participant 1 raises his hand after the first gong sounding but before the second gong sounding, the other 4 participants would be aware that number 1 raised his hand, even though they would not know the color of 1's hat. Is this true?
-
A classic puzzle notes that 3 miles of road is sufficient to connect four cities situated on the corners of a square one mile on a side. Yes, the cities are really small; point-like, for our purposes. The question is then asked: what length of road(s) is necessary to connect them? I.e. the shortest distance of road(s) required.
Here's an attempt,
Let the cities be arranged on a grid with coordinates (0,0), (1,0), (0,1), and (1,1). We draw the lines with the following shape: >-<. Essentially, we make two way points, each joining two cities. We then draw a straight line between the two waypoint.
If we let the coordinates of the waypoints be ( sqrt( 1/12), 1/2 ) and ( 1 - sqrt( 1/12), 1/2 ), then the total distance used is about 2.732.
-
I agree that each ant gets to the initial position of some ant after 10 minutes. And I agree that, since they can't actually go through each other, their initial order around the circle remains unchanged. But I don't think that requires each ant to return to its own original position -- there could be a shift of all ant positions that retains the original order.
Looking at the case of 3 ants, a shift seems quite possible, if not probable.
From examining a few smaller cases, it seems that all ants will return to their original position after 10 minutes if one of the following is true: (1) the original orientation of all ants is the same, or (2) the number of ants with an initial clockwise orientation equals the number of ants with an initial counter-clockwise orientation.
I've only taken a look at a few cases, so this might not always hold true. Can anyone prove this or come up with a counter-example?
If my previous hypothesis is true, then I think the probability in the case of 14 ants works out to 1717/8192, which is about 21%.
This is indeed the correct probability. Congrats! (14.swapnil.14 made the same conjecture but made some mistake in the calculations). However, the solution to this puzzle is slightly incomplete (for me) because the probability computation relies on the unproven fact that
The red ant would return to the original position if (1) the original orientation of all ants is the same, or (2) the number of ants with an initial clockwise orientation equals the number of ants with an initial counter-clockwise orientation.
There is a neat proof for this fact, and I think the fine denizens of the den would appreciate the challenge of working why the above statement is true. Instead of posting that fact as a new puzzle, I think I'll declare this puzzle to be half-solved, and revise the OP to include this new challenge.
-
Suppose that there is a thin, circular ring of wire with circumference of 10 meters, and that we have some ants with the following properties,
1) All the ants when placed on the wire will travel at a fixed, constant speed of 1 meter/minute in the direction that they are heading.
2) When any two ants collide on the wire, each ant will instantaneously turn around and travel in the opposite direction at the same speed.
Suppose that we simultaneously place 14 ants at random locations on the ring. The orientation in which each ant is headed (clockwise or counter-clockwise) is determined by a fair, random coin flip. 13 of the ants are colored black, and 1 of the ants is colored red. We let the ants run around the ring as specified by the conditions above. After precisely 10 minutes, what is the exact probability that the red ant will end up at the spot it started in the beginning of the game?
Extra bonus:
The red ant would always return to the original position if and only if (1) the original orientation of all ants is the same, or (2) the number of ants with an initial clockwise orientation equals the number of ants with an initial counter-clockwise orientation.
-
So sorry for the delay in getting back to this one. That darn pesky work thing compounded by holiday stuff.only briefly scanned your expression bushindo. impressive as always. personally, had to do it longhand on a spreadsheet with a bunch of cut and paste so dont doubt I may have flubbed somewhere. came up with pretty much the same - .4927945. just tried plugging in for a cut ace in your expression and get .38896? by my methodology Vern wins when all three of his cards are the same color (25/51)3 and when two of his cards are the same color 3*(25/51)2(1-25/51) or .48530. Please feel free to point out my wayward thinking. did not mean for this problem to be such an exercise in combinatorics. was hoping perhaps initially the effect of the revealed card might be ignored and the (what I thought was unexpected) odds of 50/50 with Vern having two more cards guessed as if the game was played with infinite decks of cards. a better problem would probably have just been to ask who, if anyone, had the best chance of winning and why.
First of all, let me say that this is an excellent problem. Thanks for sharing it.
For the case of the cut ace, then the face card f = 1, the additional same-color cards in Vern's hand c = 0, and the player's required same-color cards to win are p = 2 or p = 3, so according to the expression in the last post the probability of beating Vern when the cut card is an ace is
P = 25C2 * 26C1 /51C3 + 25C3 * 26C0 /51C3
= 0.3745498 + 0.1104442 = 0.484994
We can also compute the chance of Vern losing in this case using another way. As you pointed out, Vern wins when all three of his cards are the same color (25/51)*(24/50)*(23/49)= 0.1104442 and when two of his cards are the same color 3*(25/51)*(24/50)*(26/49) or .0.3745498. The total probability is then .484994, which is identical as the result from the other method.
As for the problem, the result is unintuitive to me as well. Obviously, the dependencies in card drawing would reduce Vern's chance of losing from 50% in the case of infinite decks. I thought that the dependency effect would be larger and that Vern's losing chance (P) should be in the mid 40 (and that this would be a lucrative game to play with my friends), so I was surprised to find P = 49.29124%. Again, thanks for the problem.
-
The full expression for the chance of beating Vern at this game is
Plugging this in the computer, we get P = 0.4929124
-
Here's a non-calculus guess
2/3
-
Hmm, I guess I read my choices incorrectly...nonetheless there should be a better option
you lose 4 of the first 6 games?
You didn't read the choices incorrectly. I was just being faceticious :-). Please carry on.
-
If your team is evenly matched in a best 4 of 7 series of games,
and you could be assured of winning one of the games,
which game would you choose?
This is an easy one
Game 7 =)
-
Thanks for the problem. By the way, congrats on the 1000th post.
There are lots of solutions. Here are 3 of them
p i l s b u t e r a q u e o s f n k 21 2 14 9 10 5 20 6 12 25 24 5 16 6 9 4 7 26 7 16 14 8 3 15 11 20 25 18 5 15 4 20 8 2 6 10 6 20 3 25 13 8 21 9 26 18 10 8 5 9 25 2 4 22
-
I mean that nCk is odd if and only if the binary
representation of n contains a 1 in every position
where the binary representation of k contains a 1.
So, for example, if n were 84, 1010100 in binary,
then the only values of k which would make 84Ck
odd is 0,4,16,20,64,68,80 and 84 (binary 0000000,
0000100, 0010000, 0010100, 1000000, 1000100, 1010000,
and 1010100). In terms of the way I said it in the OP,
84C20 is odd because 20 = 84 AND 20
(0010100 = 1010100 AND 0010100). I should have used
parentheses in the OP to make it k = (n AND k).
I hope this makes it clear.
Thanks for sharing these little gems with us, superprimastic. I enjoy the journey greatly, and feel enriched by the experience. Also, thanks for you recommendation. I picked up the Stanford Mathematics Problem Book for my ereader, and look forward to spending some time on it.
Background:
Some notations and general thoughts before we start the proof.
Let P( n, k ) be a binary test for a property defined as follows
P(n, k) = [ (n AND k) == k ]
In other words, P(n, k) returns TRUE if the binary representation of n contains a 1 in every position where the binary representation of k contains a 1, and FALSE otherwise. Using superprimastic's example, if n were 84, 1010100 in binary, then the only values of k which would make P( n, k) = TRUE is 0,4,16,20,64,68,80 and 84 (binary 0000000, 0000100, 0010000, 0010100, 1000000, 1000100, 1010000, and 1010100).
Let f0( m ) be the position of the right-most digit of 0 in the binary expansion of m. Let f1( m ) be the position of the right-most digit of 1 in the binary expansion of m. We consider the right-most digit of a binary number to be at position 1, and the second digit from the right to be at position 2, and so on. For instance, f0( 11001b ) is equal to 2, and f1( 11001b ) is equal to 1, where 11001b is the binary representation of the decimal number 25.
Another general thing is the process of addition and subtracting 1 to a binary number. The general observations are as follows
1) If m is a binary number, then (m-1) can be obtained by flipping all digits of m from position 1 to f1( m ).
2) If m is a binary number, then (m+1) can be obtained by flipping all digits of m from position 1 to f0( m ).
Last general thing is an identity for the binomial coefficient, which is
n+1Ck = nCk + nCk-1
So, let's get to the proof.
Claim: nCk is odd if and only if P(n, k) == TRUE
Outline of proof:
We prove this using induction. We assume that the claim is true for nCk, where k <= n. We then prove that the claim is true for n+1Ck.
Using the binomial identity, the proof then reduces to proving the following two statements
A) If P(n + 1, k ) = TRUE, then exactly one of P(n , k ) and P(n, k - 1 ) will be TRUE. [ in other words, P(n , k ) XOR P(n, k + 1 ) = TRUE ]
B) If P(n + 1, k ) = FALSE, then either
B.1) P(n , k ) = FALSE and P(n, k - 1 ) = FALSE or
B.2) P(n , k ) = TRUE and P(n, k - 1 ) = TRUE.
Part A:
Let's examine statement A,
If P(n + 1, k ) = TRUE, that implies f1( n+1) <= f1( k ), and it is easy to show* the following two statements using the process of adding and subtracting 1 from a binary number
a) If P(n + 1, k ) = TRUE and f1( n+1) = f1( k ), then P(n , k ) = FALSE and P(n, k - 1 ) = TRUE
b) If P(n + 1, k ) = TRUE and f1( n+1) < f1( k ), then P(n , k ) = TRUE and P(n, k - 1 ) = FALSE,
So, given that the claim is true for nCk under induction, the above implies that P(n + 1, k ) = TRUE leads to n+1Ck being odd.
Part B:
Let's examine statement B. Without loss of generality, we only need to show that if P(n + 1, k ) = FALSE and P(n , k ) = TRUE, then P(n , k - 1 ) = TRUE as well. We're only showing 1 direction but it can be extended both direction using the symmetry nCk = nCn - k.
So P(n + 1, k ) = FALSE and P(n , k ) = TRUE implies that f0( n ) > f1( k ). Using the process of adding and subtracting 1 from a binary number, it is easy to show* that P(n , k - 1 ) = TRUE as well.
The above implies that if P(n + 1, k ) = FALSE and one of P(n , k ) = TRUE or P(n, k - 1 ) is TRUE, then the other one is TRUE as well. This implies that if P(n + 1, k ) = FALSE, then nCk and nCk-1 are either both even or both odd, which leads to n+1Ck being even.
QED.
Note: The parts that say 'it's easy to show*' are indeed easy to work out on paper, but quite hard to explain. I'll leave it as an exercise for the reader. There are also some minor details about proving the claim for initial small values of n and k, and also showing that n+1Cn+1 is odd. Both of those are trivial claims, so I won't show it here.
-
How do I come up with my problems? Well, I like to keep a few relatively new
expository mathematics texts nearby so that I can fill some of the time slots
in my life. I routinely keep notes as I flip the pages. These notes are usually
the basis of my posted topics. Something that surprises me, like the odd binomial
coefficient thing, usually makes it in one of my topics. So, most of my topics
are not original, but some are. I find my perusal of expository texts gives me
lots of insights. I usually get these books using inter-library loan from
university libraries. I'm glad you like some of this stuff, Captain! Thanks!
Let me just chime in and say that I like your puzzles as well. I'm always happy to see new topics that you post. Can you recommend one or two of these expository texts? There are some time slots in my life that I'd like to put to better use.
-
Why is it that the binomial coefficient nCk is an
odd number if and only if, thinking of the numbers
in their binary representations, k = n AND k ?
I would like some clarification. What do you mean by 'thinking of the numbers
in their binary representations'? My interpretation is that nCk is odd if and only if n = k and k > 0, but that interpretation is clearly false. Clarification would be appreciated. Thanks.
-
What is the length of a side of an equilateral
triangle which has a point inside of it that is
at distances 3, 4, and 5 from its vertices?
This is such an elegant problem. I'm amazed at how the algebra works out nicely. Thanks
By combining 3 equations for the circles of radii 3, 4, and 5 centered at each of the 3 verteces and Heron's formula, I get the following equation for L
L4 - 50 L2 + 193 = 0
Solving for L using the quadratic formula, I get
L =[ 25 + .5*( 1728)1/2 ]1/2
-
(N!)2
I looked at a number of approaches to the problem, but it turned out to be much simpler than I initially thought (assuming I'm correct in my thinking).
First, take the identity matrix and scramble it while keeping a 1 in each row and column. There are N! of these since it is equivalent to choosing the column for the top 1, then choosing from the remaining columns for the second, etc.
Second, take a matrix with 2's along the diagonal and zeros elsewhere (e.g., 2I, where I is the identity matrix) and do the same thing. Again N!
Now add element-wise each possibility of the first scramble to each possibility for the second, and you get (N!)2 possibilities.
And just because I haven't written any proofs recently, here's an attempt. Let me know if I mess up somewhere.
Do all these satisfy the constraints? (my set is a subset of the solution set)
1. All entries are non-negative integers
The element wise addition will only result in 0's to 3's
2. Every row and every column sums to 3
Element-wise adding a matrix that had every row/column add to 1 to one that every row/column added to 2 = a matrix with every row/column adding to 3.
3. There are no more than two non-zero entries in any row and any column.
Similar reasoning to 2. Since I added element-wise two matrices that had at 1 non-zero element in each row/column, you cannot have an element-wise sum with more than two non-zero elements in a given row/column.
Does this method miss any? (the solution set is a subset of my set)
Assume I miss matrix M.
Deconstruct it into two matrices M1 and M2 by the following:
-If there is a 1 in M, put a 1 in the corresponding position in M1
-If there is a 2 in M, put a 2 in the corresponding position in M2
-If there is a 3 in M, put a 1 in the corresponding position in M1 and a 2 in the corresponding position in M2
There will be a 1 in each row/column in M1 since M must have a 3 or both a 1 and a 2 in each row/column since there can only be at most two non-zero elements that sum to 3.
This means M1 should have exactly one 1 in each column and row and zeros elsewhere, and similarly for M2 but with 2's.
Therefore M1 should have been included in the scrambling of the identity matrix, and M2 should have been included in the scrambling of the 2I matrix, so my method shouldn't have missed it and we reach a contradiction.
Since my set is a subset of the solution set, and the solution set is a subset of my set, they must be the same set.
Clear and elegant as well. Good job!
-
There is at least one initial state of
the lamps where it is impossible for
you to stop him from turning them all
on. Consider the case where the lamps
start off alternating on then off.
No mater how you rotate the table, the
lamps will get to be all on (the butler
wins) or all off, In the latter case,
the butler's next move is to list all
the chairs so that all will be turned
on no matter how you rotate the table.
I haven't checked, but there may be
other such anomalous cases.
Thanks superprismatic and witzar. That is really a silly oversight in the wording of the puzzle. The intent is to show that under certain starting lamp patterns, there is a strategy which will guarantee that the butler will never be able to turn all the lights on. I'll fix it in the OP. Thanks for pointing that out.
-
Let's say that you are setting the dining table for a party of 60 guests. The 60 guests will be seated at a giant circular table. Each seat has a lamp, and currently some of the 60 lamps are on and some are off. The butler offers to play a game with you. Let's say that the chairs are labelled with the guests names, which for convenience we label starting from the top and going clockwise as C1, C2, ..., C60, and the chairs are stationary. The giant circular dining table along with the lamps, however, can rotate. Each lamp has a switch, and flipping the switch when the lamp is on turns it off, and vice versa. The game is as follows
1) The game consist of turns. At each turn, the butler tells you a list of chairs at which he want to switch the lamps' state.
2) You will then has the option of arbitrarily rotating the entire table before applying the switches at the list of chairs in point 1). Please note that the you must rotate the table in such a way that each chair is directly across from a lamp (rotating so that a lamp ends up midway between two chairs isn't allowed). You can turn the table in any direction and for as many spaces as you want before applying the switches.
3) You may take as many turns as you'd like. If the butler succeeds in turning all the lights on, he wins.
Show that under certain starting lamp patterns, there is a strategy which guarantees that the butler will never be able to turn all the lights on.
EDIT: added the proper initial constraints thanks to superprimastic and witzar.
-
It is not possible. Think about 5x4 grid as a chessboard with 10 black squares and 10 white squares. Now try to paint with black and white tiles A-E. Each tile except D will have 2 white squares and 2 black squares, no matter how you paint it. But tile D will have 3 black and 1 white or 3 white and 1 black. Therefore it is not possible to cover with tiles A-E an area with the same number of white and black squares.
That's brilliant, witzar. Good work!
-
H = 500000 is more likely by a long shot, over 1020 times more likely, in fact
-
Here's a 4×5 grid made up of squares:
-------------------------- | | | | | | -------------------------- | | | | | | -------------------------- | | | | | | -------------------------- | | | | | | --------------------------
And here are 5 shapes, each made out of 4 squares:Shape A: ------ | | ---------------- | | | | ---------------- Shape B: ----------- | | | ---------------- | | | ----------- Shape C: --------------------- | | | | | --------------------- Shape D: ------ | | ---------------- | | | | ---------------- Shape E: ----------- | | | ----------- | | | -----------Can you fill the 4×5 grid with these
five shapes? You are allowed to flip
them and/or rotate any or all of them.
Some thoughts, mostly 90% hand waving and 10% proof by exhaustion
I don't think it is possible to perform this task. I wish I had an elegant proof, but unfortunately I don't. We'll just have to make do with proof by exhaustion.
The first thing we need to do is reason where shape C would go. Shape C could be placed horizontally or vertically. So let's examine the two cases
1) If C is placed vertically, then it will take 1 entire column of the 4x5 grid. The optimal placement in this case would be at either end, and the problem reduces to placing shape A, B, D, and E on a 4x4 grid.
a) Now the problem is where to place shape E on this 4x4 matrix. Because of rotations, there are really only 3 choices
b) In each of the 3 cases above, we can easily work through the remaining 3 pieces and show that they don't fit.2) If C is placed horizontally, then it must be placed at either the topmost of bottom-most row. It is easy to see that placing C in row 2 or 3 would fail to lead to a solution. So, let's say that we place C at the bottom row. There are 3 choices from here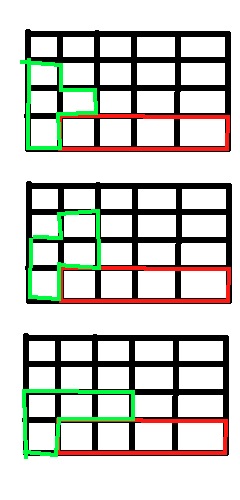
a) It is easy to work through the remaining cases and show by exhaustion that the task required by the OP is not possible. -
Adding the proof to complete the puzzle. Please excuse the formatting; typing a proof in the brainden editor is quite complicated.
See post and for background.
Lemma = Given that (1- A64m ) = 0 (see hint 2 in post #12) , then (1- Am )64 = 0 for m in the discrete set (0, 1, ..., 63 ).
Proof: (I- Am )64 = [ (I - Am)2 ]32
= [ I - 2 Am- A2m]32#comment#2 Am =0 and A = -A since we are working with binary modular arithmetic= [ I - A2m]32Repeat the process 5 more times, and we get (1- Am)64= 0.Claim: The optimal strategy for the game in the OP will eventually win in at most [ 64 (64-1) + 1 ] turns.Proof: The optimal strategy, when applied to a game with r turns, corresponds to the following matrix operations (see post #11 for background)yc= ( I - Aar).........( I - Aa2)( I - Aa1) y , where ai is the rotation amount that the butler does at turn i.After [64(64-1) + 1] turns, by the pigeon hole principle, some rotation by m spaces must have been used 64 times. Since our matrix operator is communicative (see hint 1 of post), thenyc= ( I - Am)64......... yyc= 0 * ............. y by the lemma.
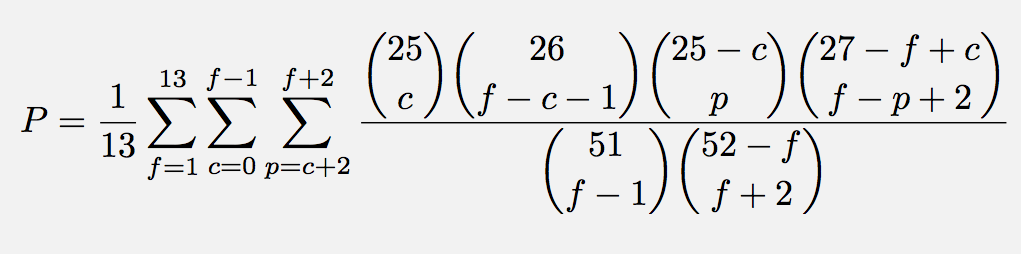
A simple (*not* bonanova 'simple') hat problem
in New Logic/Math Puzzles
Posted · Edited by bushindo
Ah, I see what you are getting at then. Your claim is absolutely right. This is a superbly designed puzzle, by the way.