-
Posts
719 -
Joined
-
Last visited
-
Days Won
5
Content Type
Profiles
Forums
Events
Gallery
Blogs
Posts posted by bushindo
-
-
I am uncertain, what uncertain means in this context.
Cole's first shot strategy is clear. He must shoot himself in the foot thus exiting the duel with a non-fatal injury. (Hopefully, he does not miss.)
Coles probability to hit the target is
c; Bobby's probability -- is b.Let's calculate the probability of Cole's survival in one on one duel with Bobby, where Cole shoots first.
X = c + (1-c)(1-b)X
X = c/(b+c-bc)
If Cole's first shot is in the air, Bobby shoots at Alex. If Bobby misses, Alex kills Bobby and Cole has one shot at Alex. If Bobby hits Alex, then a duel between Cole and Bobby ensues with Cole going first. Cole's probability of survival in this scenario is:
(1-b)c + bc/(b+c-bc).
If Cole shoots at Alex and misses, thereafter the probability is the same as as with shooting in the air. If Cole hits Alex, then he has a duel with Bobby shooting first. If survival chances in such duel are worse compared to shooting in the air, it is to Cole's advantage to shoot in the air.
If Bobby misses Cole on his first shot, it becomes a duel with Cole shooting first. Therefore Cole's surviving probability(air shot) > probability(Bobby-Cole duel) is as following:
(1-b)c + bc/(b+c-bc) > (1-b)c/(b+c-bc)
Solving we get:
c > 1 - b/(1-b)2
When b >= 39% the expression yields a negative number, meaning Cole must shoot in the air. For b <= 31% the expression is greater than 31%, which contradicts the condition that Cole is a worse shot than Bobby. That means Cole must try and shoot Alex. For b between 31% and 39%, Cole must carry out calculations and comparison before shooting.
Yes, that is the answer. Nice job.
Cole must not shoot first at Bobby,
Alex and Bobby must always shoot the higher ranking opponent.
Cole shoots first at Alex.
If Cole's survival probability for hitting Alex is the same as for missing Alex,
then Cole's strategy is uncertain: should he try to hit Alex? Or to miss him?
The critical probabilities are P(B C) and P(B C).
Duels that involve Alex are trivial.
If qX = 1-pX then
P(B C) = (1 - qB) / (1 - qBqC)
P(B C) = (1 - qC) / (1 - qBqC)
If Cole hits Alex, Cole survives with probability 1 - P(B C)
If Cole misses Alex, Cole survives with probability pBP(B C) + qBpC.
Equating these and simplifying gives qC = (1 - qB)/q2B
Now qB < qC, and both must lie between 0 and 1.
It boils down to how (in)accurate Cole is.
The extremes are totally inept and as good as Bobby.
Totally inept: qC = 1 this gives qB = .618.
As good as Bobby: qC = qB this gives qB = .683
.
So, If Cole's strategy is uncertain, then we know that Bobby's shooting accuracy lies between .317 and .382.
I believe the above solution conflates "trying to hit Alex" with "actually hitting Alex". Here is my reasoning
In the beginning before even taking a shot, Cole has two choices for strategy, either "shoot first at Alex" or "shoot into the air (deliberately missing)". (Note that if Cole is constrained to only shoot at Alex and see the shot outcome, then he doesn't really have a strategy). The solution of the puzzle is to compute and solve the following equation
[1] P( Cole win | Cole shoot first at Alex) = P( Cole win | Cole shoot first into air )
However, the solution above I think conflates "attempting to shoot at Alex" with "actually hitting Alex". From above, I annotate the given terms with what they actually mean
>> If Cole hits Alex, Cole survives with probability 1 - P(B C) => P( Cole win | Cole shoot first at Alex AND Cole hits Alex )
>> If Cole misses Alex, Cole survives with probability pBP(B C) + qBpC => P( Cole win | Cole shoot first into air )
So, the solution above actually solves the following equality
[2] P( Cole win | Cole shoot first at Alex AND Cole hits Alex ) = P( Cole win | Cole shoot first into air )
But this is not the quantity that we need to solve for, and the equality in [2] is comparing apples to oranges. The term on the left should be P( Cole win | Cole shoot first at Alex ), which can be expressed as
P( Cole win | Cole shoot first at Alex ) = pc * P( Cole win | Cole shoot first at Alex AND Cole hits Alex ) * (1- pc) P( Cole win | Cole shoot first at Alex AND Cole does not hit Alex )
P( Cole win | Cole shoot first at Alex ) = (1-pc)pc pb/[ 1 - (1 - pc)(1-pb) ] + (1-pc) (1-pb) pc + pc pc (1-pb)/[ 1 - (1 - pc)(1-pb) ]
So, if we replace the proper term P( Cole win | Cole shoot first at Alex ) into equation [1], we should get a different answer, which Prime gave in
I saw that the above analysis also uses a different meaning for P(.) compared to its usage in so I want to clarify that so we don't have any unnecessary confusion when going back and forth between the analyses.
In Post 3, P(.) is always assumed to be the probability of Cole winning, regardless of who has the first shot.
In the above quoted analysis, P(.) seems to give the probability of winning for whoever has the first shot.
-
Okay, so earlier we found that not allowing an airshot on Cole's turn reduces to a trivial solution. So, let's assume that on the first shot, Cole has the option of shooting A, B, or none of those two.
We already found that the probability of Cole winning if he shoots at A first is
WA = (1-pc)pc pb/[ 1 - (1 - pc)(1-pb) ] + (1-pc) (1-pb) pc + pc pc (1-pb)/[ 1 - (1 - pc)(1-pb) ]
By the same derivation process, we can see the probability of Cole winning if he shoots at the air first is
WN = pbpc/[ 1 - (1-pb)(1-pc) ] + (1-pb) pc
So, if we set WN = WA and solve for pb and pc, we see that both strategies are equally beneficial for Cole (hence the uncertainty, I suppose) when
pc = ( pb3 - 3pb + 1)/( pb-1)2
If it was
pb2 (square instead of cube,) our results would match.pc = ( pb2 - 3pb + 1)/( pb-1)2
Indeed it should be a quadratic expression instead of cubic. My mistake. Good catch, Prime.
-
I wouldn't post this puzzle if the answer was the same as the original Bonanova's puzzle
After some more thoughts about this problem, I think I found my source of confusion and am ready to take another stab at the answer
I think the key here is that there are several different estimates of N, depending on what kind of property you want your estimate to have. Under the requirement that our estimate of N has "the highest likelihood of being correct", then I think the previous answer in post 2 (N = max{ p1, p2, p3, p4, p5} ) is still correct.
Perhaps an example would make it clear the different types of estimates one can have. Suppose that we have a coin labelled 0 and 1 on the two sides. The coin is biased such that it would land on the 1 face 3/4 of the time. If we want the estimate of the next flip that has the highest likelihood of being right, we would choose 1. However, if we want an estimate of the flip, x, that minimizes the squared error between the flip value and x, we would choose x = .75.
I was originally convinced that my previous Bayesian formulation is incorrect, but was unable to find the error in the reasoning. I tried re-deriving the Bayesian answer by conditioning on the summary statistics max{ p1, p2, p3, p4, p5} instead of the set { p1, p2, p3, p4, p5}, and I got the same answer as before. So, apparently that Bayesian formulation is correct.
It then occurred to me that we might be thinking of different estimator for N as the solution. From earlier, we found that
P( N | { p1, p2, p3, p4, p5} ) is proportional to 1/NC5 for N between max{ p1, p2, p3, p4, p5} and infinity.
Then it makes sense that the N with the highest likelihood of being correct is N = max{ p1, p2, p3, p4, p5}. This is known as the maximum a posteriori estimate, so
Nmax_posteriori = max{ p1, p2, p3, p4, p5}
However, if the OP had asked for the estimate of N such that we minimize the squared difference between N and our estimate (see minimum mean error estimate), then the answer would have been the posterior mean of the function P( N | { p1, p2, p3, p4, p5} )
Nmin_squared_error = sum( P( N | { p1, p2, p3, p4, p5} ) * N ) for N from max{ p1, p2, p3, p4, p5} and infinity.
For instance, let's look at a concrete examle. Let's say we sampled 5 points, and they are (50, 14, 26, 4, 24). Then,
Nmax_posteriori = max{50, 14, 26, 4, 24} = 50
Nmin_squared_error = sum( P( N | { p1, p2, p3, p4, p5} ) * N ) to infinity = 65.32685. (Note the non-integer nature of this estimate. This guarantees that this guess of N will never be precisely correct since N is an integer)
For some posterior distribution (e.g., gaussian), the Nmax_posteriori and Nmin_squared_error are the same. But apparently, they are different in this situation. The requirements on the estimate of N in the OP ("the highest likelihood of being correct") points towards the maximum a posteriori estimate as the solution, though.
-
A twist on the "truel" puzzle - a duel among three participants, where shots are taken in turn.
Alex always hits his man.
Bobby is not perfect, but he shoots better than Cole does.
The referee thus gives Cole the first shot, followed by Bobby and Alex in that order.
When a man is hit, he drops out [or drops dead].
The shooting continues in sequence until only one man is unhit.
Cole does not want to take Bobby out of the competition, then Alex will hit Cole. Game over.
But it may not be wise for Cole to hit Alex either. Cole is disadvantaged in an ordinary duel.
So Cole's first-shot strategy is uncertain.
Given that it is uncertain, what can we determine regarding Bobby's shooting accuracy?
Assume each knows the others' accuracy level.
px = probability that x will hit his man.
pAlex = 1 > pBobby > pCole.
For some values of pBobby, Cole's first-shot strategy is certain.
For example, if pBobby = 0.0001, Cole tries to hit Alex and have a long almost-50% duel with Bobby..
For what values of pBobby is Cole uncertain of what to do on his first shot?
Assuming each participant is forced to shoot only at remaining duelists, then here's what I get
Intuition says that C should shoot A first. Let's go through the game tree and in what situation does C become uncertain.Let's denote the participants by A, B, and C. Let's write down the probability of C winning at the beginning of the game as P( C, B, A), where the identity of the remaining participants are listed as arguments of the function P( ), and the underlined C indicates that C has the first shot. If there are only two participants left, then we can write out the corresponding win percentagesP( C, B ) = ( 1-pb)pc/[ 1 - (1 - pc)(1-pb) ]P( C, B ) = pc/[ 1 - (1 - pc)(1-pb) ]P( C, A ) = pcP( C, A ) = 0.Now, we start off the the logic that A will always shoot the remaining person(s) with the highest hit probability. Therefore, B will always shoot the remaining participant with highest hit probability as well.I drew out two game tree for two cases- one where C chooses to shoot B first and one where C shoots A first. The game trees are hereCombining the game trees above with the two-participant results in the beginning, we can write down the winning chances for C from the two strategies. Let WA be the winning chance for C if he shoots A first, and let WB be the winning chance if he shoot B first, the probabilities areWB = (1-pc)pc pb/[ 1 - (1 - pc)(1-pb) ] + (1-pc) (1-pb) pcWA = (1-pc)pc pb/[ 1 - (1 - pc)(1-pb) ] + (1-pc) (1-pb) pc + pc pc (1-pb)/[ 1 - (1 - pc)(1-pb) ]orWA = WB + pc pc (1-pb)/[ 1 - (1 - pc)(1-pb) ]So, we see that shooting A first increases the winning probability by the amount pc pc (1-pb)/[ 1 - (1 - pc)(1-pb) ]. Now, the only way to make C uncertain is to let pc = 0, at which point his winning chance is the same regardless of who he shoots. But if his hitting probability is 0, he's screwed either way.Okay, so earlier we found that not allowing an airshot on Cole's turn reduces to a trivial solution. So, let's assume that on the first shot, Cole has the option of shooting A, B, or none of those two.
We already found that the probability of Cole winning if he shoots at A first is
WA = (1-pc)pc pb/[ 1 - (1 - pc)(1-pb) ] + (1-pc) (1-pb) pc + pc pc (1-pb)/[ 1 - (1 - pc)(1-pb) ]
By the same derivation process, we can see the probability of Cole winning if he shoots at the air first is
WN = pbpc/[ 1 - (1-pb)(1-pc) ] + (1-pb) pc
So, if we set WN = WA and solve for pb and pc, we see that both strategies are equally beneficial for Cole (hence the uncertainty, I suppose) when
pc = ( pb3 - 3pb + 1)/( pb-1)2
-
I take it in such a way that 4 ships are connected to a 5th ship from 4 sides to give it the energy all the trip ,i.e. only the central ship will be functioning and the others adhering to it are as energy suppliers only.
Your proposal (tethering 4 ships to the 5th) is akin to increasing the mass of the 5th ship by five times while also increasing the fuel tank five times. Your solution assumes that fuel usage for the navigating ship is the same whether it is alone or whether it has 5 times the mass. In physics, as in life, there is no such thing as a free lunch. You can't carry 5 times the mass to Mars without expending extra energy.Perhaps you are thinking that the navigating ship only has to set a course for the entire fleet, so the energy usage is independent of the mass. Recall that in space, if you need to change the course, you will need to change the momentum vector of the entire fleet. That means if you want to move 1 degree to the left, for example, the navigating ship will need to provide enough thrust (energy) to move its entire mass to the left that much.Even if we allow the conservation-of-energy violation, the 5 ships still can not make it to Mars and back. From your OP, "each spaceship has a fuel capacity to allow it to fly exactly 1/4 way to Mars" and "Each spaceship must have enough fuel to return safe to the base space station". Since each tank will take you 1/4 of the way to Mars, 5 tanks are enough for 1.25 of the distance to Mars. How are your 5 ships supposed to get to Mars and get home on 5 tanks? -
A twist on the "truel" puzzle - a duel among three participants, where shots are taken in turn.
Alex always hits his man.
Bobby is not perfect, but he shoots better than Cole does.
The referee thus gives Cole the first shot, followed by Bobby and Alex in that order.
When a man is hit, he drops out [or drops dead].
The shooting continues in sequence until only one man is unhit.
Cole does not want to take Bobby out of the competition, then Alex will hit Cole. Game over.
But it may not be wise for Cole to hit Alex either. Cole is disadvantaged in an ordinary duel.
So Cole's first-shot strategy is uncertain.
Given that it is uncertain, what can we determine regarding Bobby's shooting accuracy?
Assume each knows the others' accuracy level.
px = probability that x will hit his man.
pAlex = 1 > pBobby > pCole.
For some values of pBobby, Cole's first-shot strategy is certain.
For example, if pBobby = 0.0001, Cole tries to hit Alex and have a long almost-50% duel with Bobby..
For what values of pBobby is Cole uncertain of what to do on his first shot?Assuming each participant is forced to shoot only at remaining duelists, then here's what I get
Intuition says that C should shoot A first. Let's go through the game tree and in what situation does C become uncertain.Let's denote the participants by A, B, and C. Let's write down the probability of C winning at the beginning of the game as P( C, B, A), where the identity of the remaining participants are listed as arguments of the function P( ), and the underlined C indicates that C has the first shot. If there are only two participants left, then we can write out the corresponding win percentages. Note that P( . ) always indicate the probability of C winning.P( C, B ) = ( 1-pb)pc/[ 1 - (1 - pc)(1-pb) ]P( C, B ) = pc/[ 1 - (1 - pc)(1-pb) ]P( C, A ) = pcP( C, A ) = 0.Now, we start off the the logic that A will always shoot the remaining person(s) with the highest hit probability. Therefore, B will always shoot the remaining participant with highest hit probability as well.I drew out two game tree for two cases- one where C chooses to shoot B first and one where C shoots A first. The game trees are hereCombining the game trees above with the two-participant results in the beginning, we can write down the winning chances for C from the two strategies. Let WA be the winning chance for C if he shoots A first, and let WB be the winning chance if he shoot B first, the probabilities areWB = (1-pc)pc pb/[ 1 - (1 - pc)(1-pb) ] + (1-pc) (1-pb) pcWA = (1-pc)pc pb/[ 1 - (1 - pc)(1-pb) ] + (1-pc) (1-pb) pc + pc pc (1-pb)/[ 1 - (1 - pc)(1-pb) ]orWA = WB + pc pc (1-pb)/[ 1 - (1 - pc)(1-pb) ]So, we see that shooting A first increases the winning probability by the amount pc pc (1-pb)/[ 1 - (1 - pc)(1-pb) ]. Now, the only way to make C uncertain is to let pc = 0, at which point his winning chance is the same regardless of who he shoots. But if his hitting probability is 0, he's screwed either way. -
Probably not what you were looking for, but here's what I recommend Cole doCole should shoot into the air (i.e. not shoot Alex or Bobby) on his turn. Bobby and Alex will shoot one another in sequence. Cole then has the nice advantage of having the first shot on whoever survives between Alex and Bobby.So, clarification please. Can any participant choose to shoot into the air instead of the other duelists?
-
I wouldn't post this puzzle if the answer was the same as the original Bonanova's puzzle
You're right
I'm convinced that the answer, as you say, is not the same as bonanova's answer. My previous answer is incorrect, but I have yet to locate the faulty reasoning. Back to the drawing board.
-
Here is a modified version of Bonanova's puzzle
Suppose n tickets numbered 1-n are in a box, and you draw five of them without putting them back in the box.
Your tickets have numbers p1, p2, p3, p4 and p5 on them.
You don't know how many tickets are in the box, but you are asked to estimate how many there are.
What estimate of n has the highest likelihood of being correct?
Here's an answer
We wish to find P( N | p1, p2, p3, p4, p5). Let's assume that we have a prior distribution P(N). Also, the probabilities of the obtained number given N is P( p1, p2, p3, p4, p5 | N ) = 1/( NC5). So, here's the Bayesian derivations
So, if we have P(N), the derivation above is straightforward.
We are not given P(N), so let's assume that N is uniformly distributed between max( p1, p2, p3, p4, p5 ) and infinity. Unlike the previous bonanova puzzle, under this improper prior assumption, the denominator term in the equation above converges. Then P( N | p1, p2, p3, p4, p5) is proportional to 1/( NC5), which implies that we should pick N = max( p1, p2, p3, p4, p5 ).
-
Bushindo, Thanks.
I learn so much from you.
Is there also a maximum likelihood estimate of the underlying assumptions
that would make the maximum likelihood estimate of n well defined?
Thanks for the kind words, bonanova, I also learned much from you over the years. The two wonderful examples (among many) that come quickest to mind are Hole in a Sphere and Maiden Escape, both of which taught me completely new ways of thinking.
The comment I made earlier is that the solution to this puzzle will depend on what kind of prior information (or assumption) we have about the probability distribution P(N), since the Bayesian derivation forces us to explicitly use P(N) in the calculation of the answer.
My interpretation of what you are asking is that is there a maximum likelihood estimate for the distribution P(N) such that P(N|p) is well-defined (and my impression is that this is a way to bypass the requirement to know exact values for P(N)). It is possible to assume the distribution P(N) as belonging to some well-defined probability class (exponential, gaussian, negative exponential, etc.) and then use maximum likelihood to find the best-fit curve within the assumed class. Of course, there is no free lunch. We just moved the prior assumption backwards a bit so that we make assumptions about the class of probability curves P(N) belongs to.
You may be asking is there a maximum likelihood estimate for estimating what class of probability function P(N) most likely is in, and that is a much tougher problem. If we have several candidate probability classes (again, exponential, binomial, gaussian, etc.) then we can easily compare between them and find the most likely probability class for P(N). The problem is that there are an infinite number of possible probability class (and most don't have nice tractable parametric forms), and finding the best class over this domain is not possible. So, if we restrict the possible probability classes to a finite number (note that we are making some assumptions here again), we can then solve the problem.
-
I picked p in my draw. Lets estimate n = p. What would have been the likelihood that I got the max number ? : 1/p
If say n = p+1. What would have been the likelihood I picked p in my draw ? : 1/(p+1)
1/p > 1/(p+1).
So given that I picked p , the estimate of n that would give the best probability of me picking p is p itself.
So best estimate of n is p
>
Suppose n tickets numbered 1-n are in a box, and you draw one of them
You don't know how many tickets are in the box, but you are asked to estimate how many there are.
Your ticket has the number p on it.
What estimate of n has the highest likelihood of being correct?
It must be p only because then the Probabability of picking out p = 1/p, for n>p, the probability decreases.
You are both correct.
 bona_gold_star.gif
bona_gold_star.gifnakulendu posted first, so I marked his answer as the solution.
The solutions above are making some assumptions about the properties of underlying distribution of N, which may or may not be warranted depending on your interpretation of the OP.
Implicit within the explanations above is the assumption that P(N) = P(N+1). The explanation goes on to say that since P(p|N) decreases as N increases (without bound, presumably), then it makes sense that p is the most optimal choice.
From an earlier post, the full Bayesian expression for P(N|p) is
Note that if we assume that that N is uniformly distributed between p and infinity (which is an improper prior distribution), then the denominator of the term above becomes the harmonic series, which does not converge. If we assume that N is uniformly distributed between p and some large finite M, then the solution is warranted.
So, choosing N=p is the correct solution IF P(N) is uniformly distributed AND P(N) -> 0 as N approaches infinity.
-
Suppose n tickets numbered 1-n are in a box, and you draw one of them
You don't know how many tickets are in the box, but you are asked to estimate how many there are.
Your ticket has the number p on it.
What estimate of n has the highest likelihood of being correct?
It seems like this problem is dependent upon what is a reasonable a priori distribution for N.
Let P(N) be the prior distribution for the number N. Let P(p|N) be the conditional probability for p given N; we know that P(p|N) = 1/N. We wish to compute the conditional probability P(N|p), which can be expanded using Bayes theorem
So, if we are given a well-defined probability function P(N), we can easily compute the number N that gives that maximum probability P(N|p).
The problem is that we are not given what P(N) is. One reasonable choice would be to assume that P(N) is the improper uniform distribution from p to infinity (every number has an equal chance of occuring). However, if we plug that improper distribution into the equation above, we would be able to cancel out P(N), but we'd end up with a harmonic series in the denominator, which does not converge.
Oh wait, the answer is much simpler than that. Turns out this is the easiest bonanova puzzle I have ever seen =)
Since "n tickets numbered 1-n are in a box", if we get number p = (1-n), then it is easy to see that n = 1 - p.
-
Suppose n tickets numbered 1-n are in a box, and you draw one of them
You don't know how many tickets are in the box, but you are asked to estimate how many there are.
Your ticket has the number p on it.
What estimate of n has the highest likelihood of being correct?
It seems like this problem is dependent upon what is a reasonable a priori distribution for N.
Let P(N) be the prior distribution for the number N. Let P(p|N) be the conditional probability for p given N; we know that P(p|N) = 1/N. We wish to compute the conditional probability P(N|p), which can be expanded using Bayes theorem
So, if we are given a well-defined probability function P(N), we can easily compute the number N that gives that maximum probability P(N|p).
The problem is that we are not given what P(N) is. One reasonable choice would be to assume that P(N) is the improper uniform distribution from p to infinity (every number has an equal chance of occuring). However, if we plug that improper distribution into the equation above, we would be able to cancel out P(N), but we'd end up with a harmonic series in the denominator, which does not converge.
-
Indeed, this number is a bit smaller than the one I found.
Perhaps, it is easier to evaluate as 410000...000214: "41", 97 zeros, and "214" (which is, clearly, divisible by 7) multiplied by 100 "1"s.
But where is the proof that it is the smallest number that meets the conditions?
I can't prove that it is the smallest number. The solution that you posed made me realize that my solution is flawed. Originally, I thought I had a divisibility rule for 100 ones, which allowed me to compute the smallest integer within those rules. The number you came up with made me realize that the divisibility rule I had only worked on a subset of the possible divisors.
So, there might be smaller solutions out there. I made a mistake in an earlier post. I should have called that number "the smallest number that I could find" instead of calling it the solution.
-
Excellent work so far. Sorry for not responding earlier. I was on a vacation and didn't have access to a computerI found this interesting 102-digit number: 490000...000077 (“49”, followed by 98 zeros, followed by “77”.) If you multiply that number by 111...111 (one hundred 1-s), the resulting 201-digit number:
54444...4447555...55547 (“5”, followed by 99 “4-s”, followed by “7”, followed by 98 “5-s”, followed by “47”) meets the conditions set forth in the OP, except I cannot guaranty it is the smallest number that does. (I did not find any simple combination of "1-s" and "0-s", which multiplied by all "7-s" would yeild "4-s", "5-s", and "7-s", while avoiding "8-s".)On a side note. While playing with these numbers I found a simple yet curious divisibility rule, of which I was not aware before. I should try and construct a problem based on it.
The number above indeed satisfies the conditions giving in the OP, but there is a smaller number. The number I have in mind is a 201-digit number, but the 201-th (leftmost) digit is a 4.
I'm interested in seeing a puzzle based on the divisibility rule you found. For what it is worth, I also based this puzzle on a divisibility rule as well.
Solution to the puzzle
If we multiply 100 7's with the following number
58 571 428 571 428 571 428 571 428 571 428 571 428 571 428 571 428 571 428 571 428 571 428 571 428 571 428 571 428 571 428 571 428 602
We would get the following 201-digit number
455 555 555 555 555 555 555 555 555 555 555 555 555 555 555 555 555 555 555 555 555 555 555 555 555 555 555 555 555 555 555 555 555 747 777 777 777 777 777 777 777 777 777 777 777 777 777 777 777 777 777 777 777 777 777 777 777 777 777 777 777 777 777 777 777 777 754
If you look closely at the number above, you might be able to see the divisibility rule used in the construction of this puzzle.
-
Yes...thats right...Thanks
If the fuel is used for guidance and anti-explosibility measures only, and not for propulsion; then all five spaceships could be flung from the moon towards Mars starting at the same time. All the ships would be tethered in such a way that adjusting the course of one would alter the course of the fleet as a whole. For the first quarter of the trip, Spaceship #1 does all of the course correction. For the second quarter, Spaceship #2; and so on until landing on Mars. Once on Mars, Spaceship # 5 redistributes it's fuel equally between all of the spaceships to power their lasers and defeat the Martians.
Dear wolfgang, the solution that you consider correct suffers from two problems: 1) It violates common understanding of thermodynamics and 2) even if we allow such violation, it does not satisfy the conditions in your original post. Here is why
From your original post, each ship needs to make constant trajectory corrections since "without fuel the spaceship will miss its direction". The solution that you accept states that 4 space-ships can "piggy-back" on the course correction ability of 1 ships. That is, the ships would be tethered in such a way that adjusting the course of 1 ship would alter the course of the whole.
Of course, a simple understanding of physics would indicate that we don't really save any fuel if we allow 1 ship to change the course for all 5. If a single ships needs to make a minor course correction, it would need to provide enough thrust (energy) to move its mass however much required. If a single ship is tethered to 4 other ships, Newton's equation (F=ma) implies that the navigating ship would need 5 times the energy to alter the current course. So, in reality, tethering 5 ships together would make the single navigating ship burn fuel 5 times as fast as it changes course.
That said, even if we allow such violation, how do you suppose to get the ships home. From your OP, "each spaceship has a fuel capacity to allow it to fly exactly 1/4 way to Mars" and "Each spaceship must have enough fuel to return safe to the base space station". Even allowing for the thermodynamics violation, all your 5 ships would end up on Mars with 1 tank left, which is only good enough for 1/4 of the way back to the moon base.
While I understand that lateral and out-of-box thinking are valued around here, in general such solutions have to be internally consistent (and avoid violating explicit conditions set forth in the original post). Also, in this forum, we obey the law of thermodynamics.
-
Dear Bushindo....you should notice that I have concidered the moon as our base station(!) and not the earth.So you should think a little bit (laterally),and try to reduce the number to 5 ships only!...note : all of them will reach mars
So I guess the lateral solution of this puzzle is contingent upon the properties of this 'fuel'. My previous solution assumes that "the fuel spent is proportional to distance travelled". Since that doesn't seem to be the case, I'd like some clarification about the conditions of the puzzle.
1) My impression is that the fuel is used to make constant minor course corrections during the trip (per OP: "without fuel the spaceship will miss its direction") and to maintain the life-support and ship computer (per OP: "… and may explode"). Is this correct? If that is not correct, what is the fuel being used for?
2) Consider the following two scenarios
* A single ship flies from base (x=0) to the one-fourth point (x=1/4)
* A ship flies from the halfway point (x=1/2) to the three-fourth point (x=3/4)
Does the ship use the same amount of fuel (1 tank) in both scenarios?
3) Are the ships supposed to land on the surface of Mars?
-
Here is the amended equation that should return the desired outcome of the larger of the two input values, m or n.
This assumes a few things:
- Given m and n, the largest value presented is the minimum number of checkers needed to be placed on the board.
- The factorial of a negative number will be equal to the negative value of the factorial of that number's positive counterpart. -z! = -(z!)
- The factorial of 0 equals 1.
- I haven't messed up anywhere.
*Items 2 and 3 are supported by WolframAlpha ( 0! = 1 ; -5! = -120 ; -6! = -720 ; -7! = -5040 ; etc... ), but don't seem to be uniformly accepted elsewhere.
Comments on point 2. and 3.
The factorial of 0 is indeed 1 by convention.
As for the assumption (-z)! = -(z!) for a positive z, it is not true. Check out the gamma function, which is the extension of the factorial function to real and complex numbers. The gamma function is undefined at non-positive integers. I suspect Wolfram Alpha is interpreting your testing inputs as -1 * (z!). For instance, -1*(5!) = -120 ; -1*(6!) = -720 ; -1*(7!) = -5040.
-
Well...9 ships are too much...try to reduce the number
I don't think the number of ships can be reduced below 9. Here is why
Let's say that the moon is at location (x = 0), and Mars is at (x=1). Each ship can travel a distance of (1/4) on a full tank.
The moon base has unlimited fuel, so if we only have 1 space-ship, the max range we can reach (and return safely) is (1/4)*(1/2) = 1/8.
We can imagine that each spaceship we use can extend the fuel capacity of the base by a distance up to (but not including) 1/8. For instance, at a lesser distance of (1/9), a single spaceship can take as many trips as required to shuttle back and forth to deposit fuel at location (x=1/9). Each trip the ship can deliver 1/36 of a tank, but we can take as many trip as necessary. Note that the single ship *cannot* extend the fuel-supply to the precise distance of (1/8), as it would be not able to deposit any fuel at (x=1/8) and return home safely.
So, if a single space-ship can extend the fuel-supply line by 0 < d < 1/8, then we would need minimum of 8 ships to extend the fuel-supply line past (x=7/8). We then need 1 more ship to go to Mars and return. That makes 8+1 = 9 ships.
-
I want the fewest number of ships required , and at least one of them should launch with enough energy keeping it working.
If you want the number of unique ships required, then
You would need 9 different ships. Let's label the ships 1-9. Let the distance to Mars be 1 unit. Let the base space station be located at (x=0) and Mars be at (x=1). The idea is as follows
1) Let ships 2-9 go to the location (x = 1/9) and stay there. Ship 1 would then shuttle back and forth between the starting point (x = 0) and (x = 1/9) to deliver gas to the ships 2-9 until all 8 ships are full of gas. Each trip ship 1 can deliver 1/36 of a tank.
2) Let ships 3-9 go to the point (x=2/9). Ship 2 now shuttles back and forth between (x=1/9) and (x=2/9) to deliver gas to ships 3-9 until all are full of gas. Each trip ship 2 will have to wait at (x=1/9) for ship 1 to deliver gas to it, and then it can deliver (1/36) of a tank at (x=2/9).
3) Ship 4-9 will then proceed to point 3/9, and then ship 3 shuttles back and forth as above. Eventually ship 9 will be able to reach Mars and go back.
-
i got a bigger number
Dragons have to meet for a brainstorm in a convention center. The delegates have to be selected to provide the maximum efficiency of the brainstorm session. A dragon has any amount of heads, and for any N, any amount of N-headed dragons is available if needed. The problem is that the size of the convention center is limited so no more than 1000 heads can fit into the assembly hall. The intellectual power of a dragon pack is the product of head numbers of dragons in the pack. How should an optimum pack look like (the total number of dragons, the head number distribution)?
I'm getting the max of
333 three-headed dragons
1 one-headed dragon.
Intellectual power is 3^333
Ha, silly me
332 3-headed dragons
1 4-headed dragon
Intellectual power is 3^(332) * 4
-
Dragons have to meet for a brainstorm in a convention center. The delegates have to be selected to provide the maximum efficiency of the brainstorm session. A dragon has any amount of heads, and for any N, any amount of N-headed dragons is available if needed. The problem is that the size of the convention center is limited so no more than 1000 heads can fit into the assembly hall. The intellectual power of a dragon pack is the product of head numbers of dragons in the pack. How should an optimum pack look like (the total number of dragons, the head number distribution)?
I'm getting the max of
333 three-headed dragons
1 one-headed dragon.
Intellectual power is 3^333
-
The thing about the space travel is that it doesn't require fuel to cover the distance. The fuel is required to break free of the gravity and to establish the direction and speed. Once you're far enough from any large celestial bodies you can cover arbitrarily large distances without any fuel consumption. So the fuel consumption is not proportionate to the distance, but is proportionate to the masses of the celestial bodies you're launching from or you're in gravitational field of.
Anyway, assuming that the fuel is consumed at a constant rate for the distance travelled I have a couple of questions:
1) Does the spaceship that reaches Mars also have to return to the station?
2) Can the spaceships that return to the base be used again, and if so, then do we count the number of spaceships used or do we count the number of spaceship launches?
k-man makes a good point. For the sake of the puzzle, let's assume that the fuel spent is proportional to distance travelled. Let's also assume that the ship that gets to Mars will need to return home.
It's not clear whether the OP wants the minimum unique number of ships required or the minimum unique number of ship launches.
Let's assume that we want the minimum unique number of ships (a ship can launch more than once). I'm getting an answer of 9 ships required if we allow a ship to turn off its engine and wait for fuel; see below for an outline of the solution. This will take a *long* time, though.
Let's assume that we want the minimum number of ship launches (also the one that takes the least time to get to Mars). Here are where things get interesting.
Let the distance to Mars be 12 unit. On a full tank a ship can travel 3 units. We define a function s(d) as the number of unique launches required to put 1/3 gas tank at distance d (and have all the ships return home to base). It is easy to see that
s(1) = 1
s(2) = 3
s(3) = 9
And in general,
s(N) = 2 * ( s( 1) + s( 2 ) + … s( N - 1 ) ) + 1 = 3(N - 1 )
The above is derived by assuming for distance N, there is a special ship designated to reach distance N. At every integer distance less than N on the trip out and on the trip back, it gets (1/3) of a tank from a supporting network on other ships.
So, if we want to put (1/3) gas tank on Mars, then we would need 311 launches. Since we don't want to put any gas on Mars, we would only need 2*310.
-
Why are trailers rectangular And flower pots circular in shape? (There is a mathematical explanation)
Okay, I'll bite =)
I would guess that it is dependent on the intended function. Flower pots are intended to hold both soil and plants. The soil comes in contact with both the bottom of the pot and the sides, and thus the flower pot needs to be circular in order to distribute the horizontal force from the soil and plants evenly. A rectangular flower pot would have weak-points at the corners where the sides join, and thus would not be as optimal a design.
Trailers are rectangular because they are intended to carry their load on the floor or bottom of the enclosure. The walls of the trailers are not primarily intended for load-bearing, and thus they do not need to be circular to distribute the weight.
As a further argument, consider gas trucks that carry their liquid load in cylindrical tanks. Since the liquid gas applies pressure on both the floor and the sides of the tanks, the tanks are designed as a cylinder (actually more like a sphere elongated on 1 axis- see attached image) to prevent structural faults that would arise from uneven force distribution.




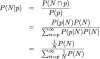
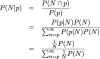

For Bushindo - (others try at your own risk)
in New Logic/Math Puzzles
Posted
I agree about semantics. I think the underlying crux of the discussion is the interpretation of 'uncertain'