-
Posts
579 -
Joined
-
Last visited
-
Days Won
8
Content Type
Profiles
Forums
Events
Gallery
Blogs
Everything posted by EventHorizon
-
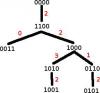
Touring the chessboard with a single die
EventHorizon replied to bonanova's question in New Logic/Math Puzzles
#include <stdio.h> #include <stdlib.h> #include <iostream> #include <memory.h> #include <vector> using namespace std; #define GRIDSIZE 8 enum dir { dir_front = 0, dir_back = 1, dir_up = 2, dir_down = 3, dir_right = 4, dir_left = 5, num_dirs = 6, dir_error = 7, dir_undo = 8 }; dir facing; dir move; vector<int> hist; int displacement = {0,0,-GRIDSIZE,GRIDSIZE,1,-1,0,0}; int startpos; dir startdir; dir tiltarray[] = {dir_error,dir_error,dir_up,dir_down,dir_right,dir_left, dir_error,dir_error,dir_down,dir_up,dir_left,dir_right, dir_error,dir_error,dir_back,dir_front,dir_up,dir_up, dir_error,dir_error,dir_front,dir_back,dir_down,dir_down, dir_error,dir_error,dir_right,dir_right,dir_back,dir_front, dir_error,dir_error,dir_left,dir_left,dir_front,dir_back, dir_error,dir_error,dir_error,dir_error,dir_error,dir_error, dir_error,dir_error,dir_error,dir_error,dir_error,dir_error}; dir tilt(dir cur, dir tiltdir) { int val = cur*num_dirs+tiltdir; return tiltarray; } void printdir(dir cur) { switch (cur) { case dir_front: cout << "1"; break; case dir_back: cout << "6"; break; case dir_up: cout << "^"; break; case dir_down: cout << "v"; break; case dir_right: cout << ">"; break; case dir_left: cout << "<"; break; default: cout << " "; break; } } void drawgrid() { for(int i = 0; i < GRIDSIZE*2+1; i++) cout << "_"; cout << endl; for(int j = 0; j < GRIDSIZE; j++) { cout << "|"; for(int i = 0; i < GRIDSIZE; i++) { printdir(facing); //printdir(move); if (i <= GRIDSIZE-2) { if ((move==dir_right) || (move==dir_left)) { cout << "="; } else { cout << " "; } } } cout << "|" << endl; if (j <= GRIDSIZE-2) { cout << "|"; for(int i = 0; i < GRIDSIZE; i++) { if ((move==dir_down) || (move==dir_up)) { cout << "|"; } else { cout << " "; } if (i < GRIDSIZE-1) cout << "X"; } cout << "|" << endl; } } for(int i = 0; i < GRIDSIZE*2+1; i++) cout << "-"; cout << endl; } int validmove(dir tiltdir, int verbose) { if (((tiltdir==dir_up)&&(hist.back()<GRIDSIZE)) || ((tiltdir==dir_down)&&(hist.back()>=(GRIDSIZE-1)*GRIDSIZE)) || ((tiltdir==dir_right)&&(hist.back()%GRIDSIZE==GRIDSIZE-1)) || ((tiltdir==dir_left)&&(hist.back()%GRIDSIZE==0))) { if (verbose) cout << "Invalid move: Boundary hit." << endl; return 0; } if (facing] != dir_error) { if (verbose) cout << "Invalid move: Repeating a square." << endl; return 0; } if ((tilt(facing,tiltdir)==dir_front) && (hist.size() != GRIDSIZE*GRIDSIZE-1)) { if (verbose) cout << "Invalid move: 1 would be facing up." << endl; return 0; } return 1; } int solved() { if ((hist.size()==GRIDSIZE*GRIDSIZE) && (facing == dir_front)) return 1; return 0; } int validmovecircuit(dir tiltdir) { if (((tiltdir==dir_up)&&(hist.back()<GRIDSIZE)) || ((tiltdir==dir_down)&&(hist.back()>=(GRIDSIZE-1)*GRIDSIZE)) || ((tiltdir==dir_right)&&(hist.back()%GRIDSIZE==GRIDSIZE-1)) || ((tiltdir==dir_left)&&(hist.back()%GRIDSIZE==0))) return 0; if (facing] != dir_error) return 0; if (tilt(facing,tiltdir)==dir_front) return 0; return 1; } int solvedcircuit(dir tiltdir) { dir nextdir = tilt(facing,tiltdir); int nextpos = hist.back()+displacement; if ((hist.size()==GRIDSIZE*GRIDSIZE) && (nextdir == startdir) && (nextpos == startpos)) return 1; return 0; } int main(int argc, char *argv[]) { hist.push_back(0); for(int i = 0; i < GRIDSIZE*GRIDSIZE; i++) { facing = dir_error; move = dir_error; } facing = dir_front; drawgrid(); int ch = 0; while (1) { if (ch != 10) cout << "Enter command (wasd,k-solve,o-circuit,' '-undo): "; ch = getchar(); dir tiltdir = dir_error; switch (ch) { case 'w'://up tiltdir = dir_up; break; case 's'://down tiltdir = dir_down; break; case 'd'://right tiltdir = dir_right; break; case 'a'://left tiltdir = dir_left; break; case ' '://undo tiltdir = dir_undo; break; case 'o'://circuit { int xpos,ypos,dirtemp; cout << "X (0-" << (GRIDSIZE-1) << "): "; cin >> xpos; cout << "Y (0-" << (GRIDSIZE-1) << "): "; cin >> ypos; cout << "dir (0-f,1-b,2-u,3-d,4-r,5-l):"; cin >> dirtemp; startdir = (dir) dirtemp; startpos = ypos*GRIDSIZE+xpos; hist.clear(); hist.push_back(startpos); for(int i = 0; i < GRIDSIZE*GRIDSIZE; i++) { facing = dir_error; move = dir_error; } facing = startdir; hist.reserve(GRIDSIZE*GRIDSIZE+1); while(hist.size() > 0) { dir nextone = dir_error; switch(move) { case dir_error: nextone = dir_up; break; case dir_up: nextone = dir_down; break; case dir_down: nextone = dir_right; break; case dir_right: nextone = dir_left; break; case dir_left: nextone = dir_undo; break; default: cout << "Should never get here!!" << endl; } if (nextone == dir_undo) { if (hist.size() <= 1) break; facing = dir_error; move = dir_error; hist.pop_back(); continue; } move = nextone; if (validmovecircuit(nextone)) { dir temp = tilt(facing,nextone); hist.push_back(hist.back()+displacement); facing = temp; move = dir_error; if (hist.size()==GRIDSIZE*GRIDSIZE) { dir dirs = {dir_up,dir_down,dir_right,dir_left,dir_undo}; for(int i = 0; i < 4; i++) { if (solvedcircuit(dirs)) { move = dirs; cout << "Found one!" << endl; drawgrid(); move = dir_error; } } } } } cout << "Done!" << endl; break; } case 'k'://solve it { int xpos,ypos; cout << "X (0-" << (GRIDSIZE-1) << "): "; cin >> xpos; cout << "Y (0-" << (GRIDSIZE-1) << "): "; cin >> ypos; startpos = ypos*GRIDSIZE+xpos; hist.clear(); hist.push_back(startpos); for(int i = 0; i < GRIDSIZE*GRIDSIZE; i++) { facing = dir_error; move = dir_error; } facing = dir_front; hist.reserve(GRIDSIZE*GRIDSIZE+1); while(hist.size() > 0) { dir nextone = dir_error; switch(move) { case dir_error: nextone = dir_up; break; case dir_up: nextone = dir_down; break; case dir_down: nextone = dir_right; break; case dir_right: nextone = dir_left; break; case dir_left: nextone = dir_undo; break; default: cout << "Should never get here!!" << endl; } if (nextone == dir_undo) { if (hist.size() <= 1) break; facing = dir_error; move = dir_error; hist.pop_back(); continue; } move = nextone; if (validmove(nextone,0)) { dir temp = tilt(facing,nextone); hist.push_back(hist.back()+displacement); facing = temp; move = dir_error; if (solved()) { cout << "Found one!" << endl; drawgrid(); } } } cout << "Done!" << endl; break; } default: break; } if (tiltdir == dir_error) continue; if (tiltdir == dir_undo) { if (hist.size() <= 1) continue; facing = dir_error; hist.pop_back(); move = dir_error; drawgrid(); continue; } if (validmove(tiltdir,1)) { move = tiltdir; dir temp = tilt(facing,tiltdir); hist.push_back(hist.back()+displacement); facing = temp; } drawgrid(); } } I will put the commands used to find them in the title of the spoiler (or just listed if nothing was found with those commands). I'll also remove solutions that are reflections and/or rotations of other solutions when found during the same command, but I'll leave the duplicates found with different commands (but they'll be in different spoiler boxes anyway). Found one! _________________ |1=>=6=< >=6 6=<| | X X X|X|X|X|X|| |>=6=< < > ^=^ <| ||X X|X|X|X X X|| |> 6=< < > v=v <| ||X|X X|X|X|X|X|| |> ^ 6=< >=6 6 <| ||X|X|X X X X|X|| |> 1 ^=^=^=^=^ <| ||X X X X X X X|| |> v=v=v v=v=v <| ||X|X X|X|X X|X|| |> 6=< 6 6 >=6 <| ||X X|X|X|X|X X|| |>=6=< ^=^ >=6=<| ----------------- Found one! _________________ |1=>=6=< >=6=<=1| | X X X|X|X X X | |>=6 6=< >=6 6=<| ||X|X|X X X|X|X|| |> ^=^ v=v ^=^ <| ||X X X|X|X X X|| |> >=6 6 6 6=< <| ||X|X|X|X|X|X|X|| |> > ^=^ ^=^ < <| ||X|X X X X X|X|| |> >=6=< >=6=< <| ||X X X|X|X X X|| |> v=v < > v=v <| ||X|X|X|X|X|X|X|| |>=6 6=< >=6 6=<| ----------------- Done! k,1,0: None for a 1 at (1,0). Found one! _________________ |v=v 1=> v=v=v=v| ||X|X X|X|X X X|| |6 6=< >=6 >=6 6| ||X X|X X X|X|X|| |^ 6=< 6=< > ^=^| ||X|X X|X|X|X X | |1 ^=^=^ < >=6=<| | X X X X|X X X|| |v=v=v=v < >=6=<| ||X X X|X|X|X X | |6=< >=6 < > v=v| | X|X|X X|X|X|X|| |6=< >=6=< >=6 6| ||X X X X X X X|| |^=^=^=^=^=^=^=^| ----------------- Found one! _________________ |>=6 1=>=6 >=6=<| ||X|X X X|X|X X|| |> ^=^=^=^ >=6 <| ||X X X X X X|X|| |> >=6=< ^=^=^ <| ||X|X X|X|X X X|| |> > 6=< 1 6=< <| ||X|X|X X X|X|X|| |> > ^=^=^=^ < <| ||X|X X X X X|X|| |> >=6=< >=6=< <| ||X X X|X|X X X|| |> v=v < > v=v <| ||X|X|X|X|X|X|X|| |>=6 6=< >=6 6=<| ----------------- Done! Found one! _________________ |>=6=< 1=>=6 6=<| ||X X|X X X|X|X|| |> 6=< 6=< ^=^ <| ||X|X X|X|X X X|| |> ^=^=^ < >=6=<| ||X X X X|X|X X | |>=6=< 6=< >=6 1| | X X|X|X X X|X|| |>=6=< ^=^=^=^ v| ||X X X X X X X|| |> v=v=v v=v >=6| ||X|X X|X|X|X|X | |> 6=< 6 6 6 >=6| ||X X|X|X|X|X X|| |>=6=< ^=^ ^=^=^| ----------------- Found one! _________________ |>=6=< 1=>=6 6=<| ||X X|X X X|X|X|| |> 6=< 6=< ^=^ <| ||X|X X|X|X X X|| |> ^=^=^ < >=6=<| ||X X X X|X|X X | |>=6 6=< < >=6=<| | X|X|X|X|X X X|| |1 ^=^ < < >=6=<| ||X X X|X|X|X X | |v >=6=< < > v=v| ||X|X X X|X|X|X|| |6 >=6 6=< >=6 6| ||X X|X|X X X X|| |^=^=^ ^=^=^=^=^| ----------------- Found one! _________________ |>=6=< 1=>=6 6=<| ||X X|X X X|X|X|| |> 6=< 6=< ^=^ <| ||X|X X|X|X X X|| |> ^=^=^ < >=6=<| ||X X X X|X|X X | |>=6=<=1 < >=6=<| | X X X X|X X X|| |v=v=v=v < >=6=<| ||X X X|X|X|X X | |6=< >=6 < > v=v| | X|X|X X|X|X|X|| |6=< >=6=< >=6 6| ||X X X X X X X|| |^=^=^=^=^=^=^=^| ----------------- Found one! _________________ |>=6=<=1 1=>=6=<| ||X X X X X X X|| |> v=v=v=v=v=v <| ||X|X X X X X|X|| |> 6 6=< >=6 6 <| ||X|X|X|X|X|X|X|| |> ^=^ < > ^=^ <| ||X X X|X|X X X|| |> >=6=< > >=6=<| ||X|X X X|X|X X | |> >=6=< > >=6=<| ||X X X|X|X X X|| |> v=v < > v=v <| ||X|X|X|X|X|X|X|| |>=6 6=< >=6 6=<| ----------------- Found one! _________________ |>=6=<=1 1=>=6=<| ||X X X X X X X|| |> v=v=v=v=v=v <| ||X|X X X X X|X|| |> 6 6=< >=6 6 <| ||X|X|X|X|X|X|X|| |> ^=^ < > ^=^ <| ||X X X|X|X X X|| |> >=6=< >=6=< <| ||X|X X X X X|X|| |> >=6=< >=6=< <| ||X X X|X|X X X|| |> v=v < > v=v <| ||X|X|X|X|X|X|X|| |>=6 6=< >=6 6=<| ----------------- Found one! _________________ |>=6=<=1 1=>=6=<| ||X X X X X X X|| |> v=v=v=v=v=v <| ||X|X X X X X|X|| |> 6 6=< >=6 6 <| ||X|X|X|X|X|X|X|| |> ^=^ < > ^=^ <| ||X X X|X|X X X|| |>=6=< < > >=6=<| | X X|X|X|X|X X | |>=6=< < > >=6=<| ||X X X|X|X X X|| |> v=v < > v=v <| ||X|X|X|X|X|X|X|| |>=6 6=< >=6 6=<| ----------------- Found one! _________________ |>=6=<=1 1=>=6=<| ||X X X X X X X|| |> v=v=v v=v=v <| ||X|X X|X|X X|X|| |>=6 >=6 6=< 6=<| | X X|X X X|X X | |>=6 >=6 6=< 6=<| ||X|X X|X|X X|X|| |> ^=^=^ ^=^=^ <| ||X X X X X X X|| |> v=v=v v=v=v <| ||X|X X|X|X X|X|| |> 6=< 6 6 >=6 <| ||X X|X|X|X|X X|| |>=6=< ^=^ >=6=<| ----------------- Found one! _________________ |>=6=<=1 >=6 6=<| ||X X X X|X|X|X|| |>=6 6=< > ^=^ <| | X|X|X|X|X X X|| |1 ^=^ < > v=v <| ||X X X|X|X|X|X|| |v=v 6=< >=6 6 <| | X|X|X X X X|X|| |>=6 ^=^=^=^=^ <| ||X X X X X X X|| |> v=v=v v=v=v <| ||X|X X|X|X X|X|| |> 6=< 6 6 >=6 <| ||X X|X|X|X|X X|| |>=6=< ^=^ >=6=<| ----------------- Found one! _________________ |>=6=<=1 >=6 6=<| ||X X X X|X|X|X|| |>=6=< 1 > ^=^ <| | X X|X|X|X X X|| |>=6=< v > v=v <| ||X X X|X|X|X|X|| |>=6=< 6 >=6 6 <| | X X|X|X X X|X|| |>=6=< ^=^=^=^ <| ||X X X X X X X|| |> v=v=v v=v=v <| ||X|X X|X|X X|X|| |> 6=< 6 6 >=6 <| ||X X|X|X|X|X X|| |>=6=< ^=^ >=6=<| ----------------- Done! Found one! _________________ |>=6=< v=v=v=v=v| ||X X|X|X X X X|| |> 1 < 6=< >=6 6| ||X|X|X X|X|X|X|| |> v < 1 < > ^=^| ||X|X|X|X|X|X X | |> 6=< v < >=6=<| ||X X X|X|X X X|| |>=6=< 6=< >=6=<| | X X|X X X|X X | |v=v < v=v > v=v| ||X|X|X|X|X|X|X|| |6 6=< 6 6 >=6 6| ||X X X|X|X X X|| |^=^=^=^ ^=^=^=^| ----------------- Done! Found one! _________________ |v=v=v=v=v=v=v=v| ||X X X X X X X|| |6=< 1=>=6=< >=6| | X|X X X X|X|X | |6=< 6=< 6=< >=6| ||X X|X|X|X X X|| |^=^=^ < ^=^=^=^| | X X X|X X X X | |v=v=v < v=v=v=v| ||X X|X|X|X X X|| |6=< 6=< 6=< >=6| | X|X X X X|X|X | |6=< 1=>=6=< >=6| ||X X X X X X X|| |^=^=^=^=^=^=^=^| ----------------- Found one! _________________ |v=v=v=v v=v=v=v| ||X X X|X|X X X|| |6=<=1 6 6 >=6 6| | X X X|X|X|X|X|| |>=6=< ^=^ > ^=^| ||X X|X X X|X X | |> 6=< 6=< >=6=<| ||X|X X|X|X X X|| |> ^=^=^ < >=6=<| ||X X X X|X|X X | |> 1 v=v < > v=v| ||X|X|X|X|X|X|X|| |> v 6 6=< >=6 6| ||X|X|X X X X X|| |>=6 ^=^=^=^=^=^| ----------------- Found one! _________________ |v=v=v=v=v=v=v=v| ||X X X X X X X|| |6=<=1 v=v=v >=6| | X X X|X X|X|X | |>=6=< 6=< 6 >=6| ||X X|X X|X|X X|| |> 6=< 6=< ^=^=^| ||X|X X|X X X X | |> ^=^=^ 1=>=6=<| ||X X X X X X X|| |> v=v=v v=v=v <| ||X|X X|X|X X|X|| |> 6=< 6 6 >=6 <| ||X X|X|X|X|X X|| |>=6=< ^=^ >=6=<| ----------------- Done! Found one! _________________ |>=6=<=1 >=6 6=<| ||X X X X|X|X|X|| |>=6=< 1 > ^=^ <| | X X|X|X|X X X|| |>=6=< v > v=v <| ||X X X|X|X|X|X|| |>=6=< 6 >=6 6 <| | X X|X|X X X|X|| |>=6=< ^=^=^=^ <| ||X X X X X X X|| |> v=v=v v=v=v <| ||X|X X|X|X X|X|| |> 6=< 6 6 >=6 <| ||X X|X|X|X|X X|| |>=6=< ^=^ >=6=<| ----------------- Found one! _________________ |v=v=v=v=v=v=v 1| ||X X X X X X|X|| |6 6=< 1=>=6 6 v| ||X|X|X X X|X|X|| |^=^ < >=6 ^=^ 6| | X X|X|X|X X X|| |>=6=< > ^=^=^=^| ||X X X|X X X X | |>=6=< > v=v=v=v| | X X|X|X|X X X|| |v=v < > 6=< >=6| ||X|X|X|X X|X|X | |6 6=< >=6=< >=6| ||X X X X X X X|| |^=^=^=^=^=^=^=^| ----------------- Found one! _________________ |v=v=v=v=v >=6=<| ||X X X X|X|X X|| |6 6=<=1 6 >=6 <| ||X|X X X|X X|X|| |^=^ v=v ^=^=^ <| | X X|X|X X X X|| |>=6 6 6 1=>=6 <| ||X|X|X|X X X|X|| |> ^=^ ^=^=^=^ <| ||X X X X X X X|| |> v=v=v v=v=v <| ||X|X X|X|X X|X|| |> 6=< 6 6 >=6 <| ||X X|X|X|X|X X|| |>=6=< ^=^ >=6=<| ----------------- Done! k,2,2: None for a 1 at (2,2). Found one! _________________ |>=6=< v=v=v=v=v| ||X X|X|X X X X|| |> 1 < 6=< >=6 6| ||X|X|X X|X|X|X|| |> v < 1 < > ^=^| ||X|X|X|X|X|X X | |> 6=< v < >=6=<| ||X X X|X|X X X|| |>=6=< 6=< >=6=<| | X X|X X X|X X | |v=v < v=v > v=v| ||X|X|X|X|X|X|X|| |6 6=< 6 6 >=6 6| ||X X X|X|X X X|| |^=^=^=^ ^=^=^=^| ----------------- Done! Found one! _________________ |v=v=v=v >=6 6=<| ||X X X|X|X|X|X|| |6 6=< 6 > ^=^ <| ||X|X|X|X|X X X|| |^=^ < ^ > v=v <| | X X|X|X|X|X|X|| |1 6=< 1 >=6 6 <| ||X|X X X X X|X|| |v ^=^=^=^=^=^ <| ||X X X X X X X|| |6=< v=v v=v=v <| | X|X|X|X|X X|X|| |6=< 6 6 6 >=6 <| ||X X|X|X|X|X X|| |^=^=^ ^=^ >=6=<| ----------------- Found one! _________________ |v=v=v=v >=6 6=<| ||X X X|X|X|X|X|| |6 6=< 6 > ^=^ <| ||X|X|X|X|X X X|| |^=^ < ^ >=6=< <| | X X|X|X X X|X|| |>=6=< 1 >=6=< <| ||X X X X|X X X|| |>=6=< 1=> >=6=<| | X X|X X X|X X | |v=v < v=v > v=v| ||X|X|X|X|X|X|X|| |6 6=< 6 6 >=6 6| ||X X X|X|X X X|| |^=^=^=^ ^=^=^=^| ----------------- Found one! _________________ |v=v=v=v >=6 6=<| ||X X X|X|X|X|X|| |6 6=< 6 > ^=^ <| ||X|X|X|X|X X X|| |^=^ < ^ > >=6=<| | X X|X|X|X|X X | |>=6=< 1 > >=6=<| ||X X X X|X X X|| |>=6=< 1=> >=6=<| | X X|X X X|X X | |v=v < v=v > v=v| ||X|X|X|X|X|X|X|| |6 6=< 6 6 >=6 6| ||X X X|X|X X X|| |^=^=^=^ ^=^=^=^| ----------------- Found one! _________________ |v=v=v=v=v=v=v=v| ||X X X X X X X|| |6 6=< 6=< >=6 6| ||X|X|X|X|X|X|X|| |^=^ < ^ < > ^=^| | X X|X|X|X|X X | |>=6=< 1 < >=6=<| ||X X X X|X X X|| |> 1 >=6=< >=6=<| ||X|X|X X X|X X | |> v >=6=< > v=v| ||X|X X X|X|X|X|| |> 6=< 6=< >=6 6| ||X X|X|X X X X|| |>=6=< ^=^=^=^=^| ----------------- Found one! _________________ |v=v=v=v=v=v=v=v| ||X X X X X X X|| |6 6=< v=v=v >=6| ||X|X|X|X X|X|X | |^=^ < 6=< 6 >=6| | X X|X X|X|X X|| |6=< <=1 < ^=^=^| ||X|X X X|X X X | |^ < v=v < v=v=v| ||X|X|X|X|X|X X|| |1 < 6 6=< 6 >=6| | X|X|X X X|X|X | |6=< ^=^=^=^ >=6| ||X X X X X X X|| |^=^=^=^=^=^=^=^| ----------------- Found one! _________________ |>=6=< v=v >=6=<| ||X X|X|X|X|X X|| |> 6=< 6 6 >=6 <| ||X|X X|X|X X|X|| |> ^=^=^ ^=^=^ <| ||X X X X X X X|| |>=6=<=1 v=v=v <| | X X X X|X X|X|| |v=v=v >=6 >=6 <| ||X X|X|X X|X X|| |6=< 6 >=6 >=6=<| | X|X|X X|X X X | |6=< ^=^=^ 1=>=6| ||X X X X X X X|| |^=^=^=^=^=^=^=^| ----------------- Done! Well, that was interesting. There were quite a few solutions in general, and a few spots with none. Note: All reflections are shown twice by the code due to two directions to start moving. o,0,0,0: None for a 1 at (0,0). o,1,0,0: None for a 1 at (1,0). o,2,0,0: None for a 1 at (2,0). o,3,0,0: None for a 1 at (3,0). o,1,1,0: None for a 1 at (1,1). Two of them.Found one! _________________ |v=v=v=v=v >=6=<| ||X X X X|X|X X|| |6=<=1=> 6 >=6 <| | X X X|X|X X|X|| |>=6=< > ^=^=^ <| ||X X|X|X X X X|| |> 6=< >=6 >=6=<| ||X|X X X|X|X X | |> ^=^=^=^ >=6=<| ||X X X X X X X|| |> v=v=v v=v=v <| ||X|X X|X|X X|X|| |> 6=< 6 6 >=6 <| ||X X|X|X|X|X X|| |>=6=< ^=^ >=6=<| ----------------- Found one! _________________ |v=v=v=v=v=v=v=v| ||X X X X X X X|| |6=<=1 >=6=< >=6| | X X|X|X X|X|X | |v=v=v > 6=< >=6| ||X X X|X|X X X|| |6 6=< > ^=^=^=^| ||X|X|X|X X X X | |^=^ < > v=v=v=v| | X X|X|X|X X X|| |v=v < > 6=< >=6| ||X|X|X|X X|X|X | |6 6=< >=6=< >=6| ||X X X X X X X|| |^=^=^=^=^=^=^=^| ----------------- Done! o,3,1,0: None for a 1 at (3,1). o,2,2,0: None for a 1 at (2,2). o,3,2,0: None for a 1 at (3,2). o,3,3,0: None for a 1 at (3,3). It turns out that there is only one circuit (unique ignoring reflections and rotations) without any 1's. (found setting die in top left corner to point right (easy to show it cannot be anything but right or down and still complete a circuit)). _________________ |>=6=< v=v >=6=<| ||X X|X|X|X|X X|| |> 6=< 6 6 >=6 <| ||X|X X|X|X X|X|| |> ^=^=^ ^=^=^ <| ||X X X X X X X|| |> v=v=v=v=v=v <| ||X|X X X X X|X|| |> 6 6=< >=6 6 <| ||X|X|X|X|X|X|X|| |> ^=^ < > ^=^ <| ||X X X|X|X X X|| |> v=v < > v=v <| ||X|X|X|X|X|X|X|| |>=6 6=< >=6 6=<| ----------------- So there are 2 solutions (unique ignoring reflections and rotations) for a circuit containing one 1, and they both happen with the 1 a knights move from a corner. And there exists a single circuit (unique ignoring reflections and rotations) without a 1. I was thinking there would be more. -

Touring the chessboard with a single die
EventHorizon replied to bonanova's question in New Logic/Math Puzzles
Yeah, it would be easy. So easy in fact... that here it is Found one! _________________ |1 v=v=v=v=v=v=v| ||X|X X X X X X|| |v 6=< v=v=v >=6| ||X X|X|X X|X|X | |6 6=< 6=< 6 >=6| ||X|X X X|X|X X|| |^=^ >=6=< ^=^=^| | X X|X X X X X | |v=v >=6=< v=v=v| ||X|X X X|X|X X|| |6 6=< 6=< 6 >=6| ||X X|X|X X|X|X | |^ 6=< ^=^=^ >=6| ||X|X X X X X X|| |1 ^=^=^=^=^=^=^| ----------------- Found one! _________________ |1 v=v=v=v=v=v=v| ||X|X X X X X X|| |v 6 6=<=1 >=6 6| ||X|X|X X X|X|X|| |6 ^=^ 6=< > ^=^| ||X X X|X|X|X X | |^=^=^=^ < >=6=<| | X X X X|X X X|| |v=v=v=v < >=6=<| ||X X X|X|X|X X | |6=< >=6 < > v=v| | X|X|X X|X|X|X|| |6=< >=6=< >=6 6| ||X X X X X X X|| |^=^=^=^=^=^=^=^| ----------------- Found one! _________________ |1=>=6=< >=6 6=<| | X X X|X|X|X|X|| |>=6=< < > ^=^ <| ||X X|X|X|X X X|| |> 6=< < > v=v <| ||X|X X|X|X|X|X|| |> ^ 6=< >=6 6 <| ||X|X|X X X X|X|| |> 1 ^=^=^=^=^ <| ||X X X X X X X|| |> v=v=v v=v=v <| ||X|X X|X|X X|X|| |> 6=< 6 6 >=6 <| ||X X|X|X|X|X X|| |>=6=< ^=^ >=6=<| ----------------- Found one! _________________ |1=>=6=< >=6=<=1| | X X X|X|X X X | |>=6 6=< >=6 6=<| ||X|X|X X X|X|X|| |> ^=^ v=v ^=^ <| ||X X X|X|X X X|| |> >=6 6 6 6=< <| ||X|X|X|X|X|X|X|| |> > ^=^ ^=^ < <| ||X|X X X X X|X|| |> >=6=< >=6=< <| ||X X X|X|X X X|| |> v=v < > v=v <| ||X|X|X|X|X|X|X|| |>=6 6=< >=6 6=<| ----------------- Done! -

Touring the chessboard with a single die
EventHorizon replied to bonanova's question in New Logic/Math Puzzles
#include <stdio.h> #include <stdlib.h> #include <iostream> #include <memory.h> #include <vector> using namespace std; #define GRIDSIZE 8 enum dir { dir_front = 0, dir_back = 1, dir_up = 2, dir_down = 3, dir_right = 4, dir_left = 5, num_dirs = 6, dir_error = 7, dir_undo = 8 }; dir facing[GRIDSIZE*GRIDSIZE]; dir move[GRIDSIZE*GRIDSIZE]; vector<int> hist; int displacement[8] = {0,0,-GRIDSIZE,GRIDSIZE,1,-1,0,0}; dir tiltarray[] = {dir_error,dir_error,dir_up,dir_down,dir_right,dir_left, dir_error,dir_error,dir_down,dir_up,dir_left,dir_right, dir_error,dir_error,dir_back,dir_front,dir_up,dir_up, dir_error,dir_error,dir_front,dir_back,dir_down,dir_down, dir_error,dir_error,dir_right,dir_right,dir_back,dir_front, dir_error,dir_error,dir_left,dir_left,dir_front,dir_back, dir_error,dir_error,dir_error,dir_error,dir_error,dir_error, dir_error,dir_error,dir_error,dir_error,dir_error,dir_error}; dir tilt(dir cur, dir tiltdir) { int val = cur*num_dirs+tiltdir; return tiltarray[val]; } void printdir(dir cur) { switch (cur) { case dir_front: cout << "1"; break; case dir_back: cout << "6"; break; case dir_up: cout << "^"; break; case dir_down: cout << "v"; break; case dir_right: cout << ">"; break; case dir_left: cout << "<"; break; default: cout << " "; break; } } void drawgrid() { for(int i = 0; i < GRIDSIZE*2+1; i++) cout << "_"; cout << endl; for(int j = 0; j < GRIDSIZE; j++) { cout << "|"; for(int i = 0; i < GRIDSIZE; i++) { printdir(facing[j*GRIDSIZE+i]); //printdir(move[j*GRIDSIZE+i]); if (i <= GRIDSIZE-2) { if ((move[j*GRIDSIZE+i]==dir_right) || (move[j*GRIDSIZE+i+1]==dir_left)) { cout << "="; } else { cout << " "; } } } cout << "|" << endl; if (j <= GRIDSIZE-2) { cout << "|"; for(int i = 0; i < GRIDSIZE; i++) { if ((move[j*GRIDSIZE+i]==dir_down) || (move[(j+1)*GRIDSIZE+i]==dir_up)) { cout << "|"; } else { cout << " "; } if (i < GRIDSIZE-1) cout << "X"; } cout << "|" << endl; } } for(int i = 0; i < GRIDSIZE*2+1; i++) cout << "-"; cout << endl; } int validmove(dir tiltdir, int verbose) { if (((tiltdir==dir_up)&&(hist.back()<GRIDSIZE)) || ((tiltdir==dir_down)&&(hist.back()>=(GRIDSIZE-1)*GRIDSIZE)) || ((tiltdir==dir_right)&&(hist.back()%GRIDSIZE==GRIDSIZE-1)) || ((tiltdir==dir_left)&&(hist.back()%GRIDSIZE==0))) { if (verbose) cout << "Invalid move: Boundary hit." << endl; return 0; } if (facing[hist.back()+displacement[tiltdir]] != dir_error) { if (verbose) cout << "Invalid move: Repeating a square." << endl; return 0; } if ((tilt(facing[hist.back()],tiltdir)==dir_front) && (hist.back()+displacement[tiltdir] != GRIDSIZE-1)) { if (verbose) cout << "Invalid move: 1 would be facing up." << endl; return 0; } return 1; } int solved() { if ((hist.size()==GRIDSIZE*GRIDSIZE) && (hist.back()==GRIDSIZE-1) && (facing[hist.back()] == dir_front)) return 1; return 0; } int main(int argc, char *argv[]) { hist.push_back(0); for(int i = 0; i < GRIDSIZE*GRIDSIZE; i++) { facing[i] = dir_error; move[i] = dir_error; } facing[0] = dir_front; drawgrid(); while (1) { int ch = getchar(); dir tiltdir = dir_error; switch (ch) { case 'w'://up tiltdir = dir_up; break; case 's'://down tiltdir = dir_down; break; case 'd'://right tiltdir = dir_right; break; case 'a'://left tiltdir = dir_left; break; case ' '://undo tiltdir = dir_undo; break; case 'k'://solve it hist.clear(); hist.push_back(0); for(int i = 0; i < GRIDSIZE*GRIDSIZE; i++) { facing[i] = dir_error; move[i] = dir_error; } facing[0] = dir_front; hist.reserve(GRIDSIZE*GRIDSIZE+1); while(!solved() && hist.size() > 0) { //if (hist.size() > GRIDSIZE*(GRIDSIZE-1)+6) //{ // drawgrid(); // getchar(); //} dir nextone = dir_error; switch(move[hist.back()]) { case dir_error: nextone = dir_up; break; case dir_up: nextone = dir_down; break; case dir_down: nextone = dir_right; break; case dir_right: nextone = dir_left; break; case dir_left: nextone = dir_undo; break; default: cout << "Should never get here!!" << endl; } if (nextone == dir_undo) { if (hist.size() <= 1) break; facing[hist.back()] = dir_error; move[hist.back()] = dir_error; hist.pop_back(); continue; } move[hist.back()] = nextone; if (validmove(nextone,0)) { dir temp = tilt(facing[hist.back()],nextone); hist.push_back(hist.back()+displacement[nextone]); facing[hist.back()] = temp; move[hist.back()] = dir_error; } } if (solved()) cout << "Found solution!" << endl; else cout << "No solution??" << endl; drawgrid(); break; default: break; } if (tiltdir == dir_error) continue; if (tiltdir == dir_undo) { if (hist.size() <= 1) continue; facing[hist.back()] = dir_error; hist.pop_back(); move[hist.back()] = dir_error; drawgrid(); continue; } if (validmove(tiltdir,1)) { move[hist.back()] = tiltdir; dir temp = tilt(facing[hist.back()],tiltdir); hist.push_back(hist.back()+displacement[tiltdir]); facing[hist.back()] = temp; } drawgrid(); } } -

Touring the chessboard with a single die
EventHorizon replied to bonanova's question in New Logic/Math Puzzles
At position 5 the 1 is on top of the die again breaking that constraint. Unless, that is, if I'm misreading the constraints. -
I assume this is in reponse to my statement about order doesn't matter. I did explain that statement in post #21. The search does depend on the set of previous guesses and responses (just not on the order of them to get to that point) to decide the next sequence of cards to guess. So if we guess all red, and we get a response (which tells us the total red and total black cards)... the search should definitely be different based on the response given (though perhaps not initially in that exact scenario... I'm not sure yet).
-
I can beat bub's 1. Just ask, "wait, how many cards are there to guess for now?" And it would be 2 to the 26th power... assuming the only possible replies were "twenty-six" or "you didn't get all of them." That problem would be like a blind person trying to solve a rubik's cube, and asking "is this it?" and the other person saying "nope." (Was it the movie UHF that had that?) Agreed. I was actually writing a similar post when I noticed Time Out already did the job before my post was ready. I thought about commenting on bonanova's "factorial or exponential" comment in that post... something about needing to confiscate an EH silver star I used the binary representation of an integer to hold the binary string guesses, and simply brute force went through each possibility. That's why it is too slow with 26 cards when going through each possible guess's value for each possible target binary string when looking for the best one (though I could speed that up if I get motivated to). I do use MIT's HackMEM method for counting the number of bits (to speed that part up), which is pretty cool. Just figured out how that works. So nothing else all that insightful in the code itself.
-
For those who read my last spoiler anyway...
-
I debated as to whether I should write the answer yet, but that's what spoiler boxes are for, right? So if you don't have a good answer to this question... don't read the spoiler! [spoiler=Don't read this unless you already know what it says ]Things on your right, stay on your right. Things on your left, stay on your left. Things above eye level, stay above eye level. Things below eye level, stay below eye level. So how, since nothing is flipped, is his/her right hand raised when your left is?
-
-
-
-
If anyone actually tests it out or uses it, let me know what you think and if you want me to add an option or change something. Edit: Also... I have no idea how it happened, but a b was capitalized (or maybe even more errors introduced) in the line "unsigned int n = (~(a ^ & mask;" in the getCorrect method. I didn't notice any other strange capitalizations introduced, but they may be there.
-
Hopefully you don't think I'm being too harsh here. It's just thought and observations before and after testing the method with my code. And speaking of code... here it is for those who know c++. Welcome to the Den
-
Edit:
-
[spoiler= ]14... and once I figure out how/why it works, I'll let you know. (cmon computer, tell me the method, not just a bunch of numbers!) This isn't necessarily the limit, but the result of a greedy search that took 14 guesses to resolve to a single guessed possibility (assuming the response given to a guess was always the one that left the most possibilities). So it might be 15, but probably not 16. Unless a greedy search doesn't produce the best strategy, which is entirely possible, then it might be 12 or 13. So I guess I'm saying 14+/-2.
-
-
-
-
-
-

Create the magic trick [1] the Intelligent Match Sticks
EventHorizon replied to bonanova's question in New Logic/Math Puzzles
-

Create the magic trick [1] the Intelligent Match Sticks
EventHorizon replied to bonanova's question in New Logic/Math Puzzles
-

Happy Pythagorean Triple Day!! Also, Mother's Day.
EventHorizon replied to EventHorizon's question in New Logic/Math Puzzles
I was rushing out the door when I posted this thread, so here's a quick clarification. When I say total dates, I meant both mother and child triples included. 'total' should have been replaced with the words 'either mother or child' or 'any type of' in front of 'Pythagorean triple' in both question 2 and 3. For question 2, I mean per century (ie, ignore wrap around, which would make the answer infinite). For question 3 and 4, I meant any number of digits for the year, so it never wraps around to 0. For question 4 it makes the answer the last one that will ever happen.