-
Posts
6975 -
Joined
-
Last visited
-
Days Won
66
Content Type
Profiles
Forums
Events
Gallery
Blogs
Everything posted by bonanova
-

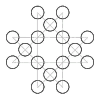
Forming a regular hexagon from a lattice
bonanova replied to BMAD's question in New Logic/Math Puzzles
-
In the all-digital future, X and O are banished from the game of tic-tac-toe. They are replaced by 1 and 0, the the result of such a game might look like this: 1 | 0 | 1 - + - + - 0 | 1 | 1 - + - + - 0 | 1 | 0 Under the usual rules that require getting 3-in-a-row, it would be a draw. But this is the digital age, and there are different rules for winning. If we sum the eight rows of three numbers we get 2, 2, 1 (horizontally) 1, 2, 2 (vertically) and 2, 2 (diagonally). Six of the sums are even, and two are odd. The final parity of the board is thus even, and the game is said to have an even outcome. If there were more odd sums than even, the game would have an odd outcome. If there were four even (and therefore four odd) sums, the game would have a neutral outcome. The game is played as follows: The winner of a fair-coin toss (call him player A) chooses whether to play first or second. The other player (call her player B) decides whether she wants an odd, even, or neutral game outcome. On each turn, a player places his choice of either a 1 or a 0 on any unoccupied place on the grid. As in normal tic-tac-toe, players alternate turns; but here on each turn a player may play either a 0 or a 1. When the places are filled, the board is examined to determine whether it is odd, even or neutral. If the final board parity matches player B's choice, player B wins; otherwise player A wins. The questions to answer are: Is there an advantage to winning the coin toss? Is there a winning strategy for either player?
-
A while ago, about a clock with indistinguishable hour and minute hands and asked at what times of day, between the hours of noon and midnight, it was impossible to unambiguously determine the time. The hands moved continuously. This puzzle asks a related question. At what times of day, between the hours of noon and midnight, is it impossible to distinguish the hands of such a clock from those of its mirror image? Clearly noon is one of these times, but not in general thereafter -- since the clock's hands will move clockwise while the hands of its mirror image will move counterclockwise.
- 1 reply
-
- 2
-

-

-
By connecting the eight vertices of an octagon (with horizontal, vertical and 45-degree lines, ignoring the perimeter) we define eight rows having either four or five points of intersection. Place sixteen consecutive (positive) integers on these points such that The sums along all eight rows are the same. The common sum is the smallest possible. A harder problem is to create the largest possible common sum.
-
Not quite. See Rainman's post for a strong clue.
-
Yeah... ... I was trying to revisit an But I couldn't find it (till just now) and did a bad job of describing the problem.
-
1 3 1 2 2 8 3 3 1 4 3 0 5 3 1 6 3 0 7 3 1 8 3 . . . .?
-
Make it easier: Solve for t.
-
With a nod to try this: Let there be an infinite sequence of exponentiation t = xx... I don't know whether that could be expressed with up arrows or not, but Rainman's arrows reminded me of this. Anyway, there is an infinite sequence of higher and higher order exponents in this expression. Show that if t = 2 then also t = 4.
-
So optimal means minimize the sum: floors+doors+ keys.
-
-
What is the relation of the ten floors to optimality? Is optimal fewest operations or shortest time? Does it take time to travel between floors? Are there n elevators ? Are you initially inside your basement office? If so can you open its door without first identifying its key and using it to get out? This is a nice puzzle.
-
-
Sounds like a homework problem. Percentages are nice - they are invariant to scale. So here's a clue: what is the percentage change in the length of the ruler?
-

Three Planet Galaxy and Stock Market Chaos
bonanova replied to BMAD's question in New Logic/Math Puzzles
-

Three Planet Galaxy and Stock Market Chaos
bonanova replied to BMAD's question in New Logic/Math Puzzles
-
Aaaargh. Up arrows are famously non intuitive to think about. I'm thinking nonetheless.
-
Perhaps, this is a valid puzzle, simply because some solved it while others didn't. I didn't solve this puzzle. I only made some observations then left it alone. Namely, the sequence of lengths seemed to be the point. As you point out it's not simple to measure them. Even if you could, you'd have to choose units that made them all integral to find the answer. If I had set out to make the effort, I probably would have taken the image into Photoshop where there is a tool for measuring lengths. But there is an easier way, even, than that. The spacings can be seen to be integers by even crude methods. From the spacings the integral lengths can be calculated, and then the answer is seen. Solving puzzles is very much about finding methods. Intuition plays a role too. There are quick-and-dirty analytical techniques that guide the process as well. For example here one can see the spacings don't vary widely. That makes primes a candidate, and rules out the Fibonacci numbers. I don't mean to be critical of your post, rather to help you get enjoyment from the broadest possible range of puzzles. Take the position that a puzzle has an answer and that it is within your grasp to find it. Let the search for a method be part of the puzzle itself. The very best puzzles uncover a simple answer to an otherwise difficult or complex question.
-
Here's a variation on a previous puzzle that let you make multiple bets while choosing the color of the next card. I shuffle an ordinary deck of playing cards and then turn over the top card sequentially so that you can see it. At any time you may ask me to stop and place a $1 bet that the next card to be exposed will be red. If you never ask me to stop, you will automatically bet on the last card. To summarize: You can bet on only one card. You don't get to choose the color. You must bet the card will be red. What is your best strategy? How much better than even can you do?
-
Sure. Drivers traveling at the speed limit or higher brake out of necessity when they encounter a traffic jam. But the same drivers are able to choose their rate of acceleration when they get to the front. Once there, the slowest of the accelerating cars dictates how quickly the cluster disperses. If the traffic density is high enough (think of Los Angeles traffic) a traffic jam sustains itself even when the initial cause is removed. It does not disperse until the traffic density drops below a threshold value and the accretion rate from behind drops below the dispersion rate in front.
-
I'll mark this solved if no one else posts a reply. Plasmid's well-described example shows that "waiting time" is a quantity that is less intuitive than first imagined. A binary number comprising random bits that takes a "long time" to happen (on average) doesn't give equal likelihood for other binary numbers to occur first. It also points out that waiting times and precedence (between two numbers) are not simple things to calculate. I'll leave the thread open in case anyone wants to find a quadruplet that is likely to precede a quadruplet having a shorter wait time. Then if anyone is interested I can share a quick method (one that I read) of getting wait times and ordering probabilities for arbitrary sequences.
-
-
Not worthy of a spoiler to observe that it's not a stick moving around a clock face (66).