bonanova

Revised answer, without need of spoiler: I now believe (with Rainman,) but cannot prove it, that in general bullets will escape. If first bullet has v=1 (possible but with zero probability) it will escape. Since bullets destroy themselves pairwise, If we could show that infinity were "even" then an even number of bullets will escape (including possibly zero.) If we could show that infinity were "odd" then an odd number of bullets will escape (guaranteeing at least one.) But infinity is not a number and does not have parity. There may be some validity to averaging the results to say that (2n-1)/2 bullets are guaranteed to escape, but I think that is specious. It's like saying the alternating series 1 - 1 + 1 - 1 + 1 - 1 + ... converges to 1/2. The partial sums are alternately 1 and 0, and in fact it does not converge at all. The question that I do not know how to answer is how efficiently a faster bullet can destroy the leading bullet if there are intervening bullets. It seems too complicated, even, to simulate. If the leading bullet has speed very close to 1, the expected number of bullets before a faster one is fired will be very large. In my previous post I said they would self-annihilate with non-zero probability. But that's not enough. If no bullet is to escape, this must happen with certainty. It is not likely that the intervening bullets will [a] be even in number and destroy each other, which would be necessary for the leading bullet to be caught. This leads me to agree with Rainman. It seems that with a high degree of likelihood bullets will escape. But it is not a proof. This is a good puzzle.

If you were to write the numbers as one, two, three, four, .... one million. What would you find?

Pickett has my vote

Our thoughts and prayers go to Michael's family in this time of great loss. SP was both a genius and a gentleman here at BrainDen. His insight and thoughtful manner graced our community almost from its inception. His passing reminds us to embrace and treasure life, and his example helps us see how to live it. Michael will be greatly missed.

Hi JS, and welcome (back) to the Den! I was thinking along the same lines

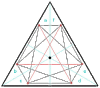
The average size of a random triangle inside any triangle is 1/12. I am assuming you mean the mean average. The average area of random triangles drawn inside any triangle T is 1/12 the area of of T. An affine transformation takes any given triangle into any other triangle while preserving relative (ratios of) areas.

Correcting an error in the simulation program, The probability that a random triangle inside an equilateral triangle covers its centroid is 0.24543 ... The average size of a random triangle inside any triangle is 1/12.

You'd have the integrals you describe in the numerator of a fraction, divided by the same integrals without the HasOrigin part in the denominator. I think that would do the normalization. Ugh, agreed.

Possibly true so long as they do not have 4-fold rotational symmetry. I should have the triangle container simulated soon.

I think for triangles with vertices either inside or on a circle the quadrant analysis applies and the result is the same. The only insight needed is to see that a line connecting points in opposite quadrants can be on either side of center with equal likelihood. I'm going to run simulations for other polygons (an equilateral-triangle containing shape seems interesting for starters) to see whether the result holds in every case. I started by dividing it into sixths and inspecting the pairs of opposing sixths. It certainly holds for a square container.

The answer is D. Since the computer plays randomly, your chance of winning does not depend on the strategy you use.

This is a test, only a test. If this were a real post, you would be required to read it, or memorize it, or pass a test on it. Since it is a test, you have no obligation whatsoever to read it, nor will there be a test. So given all that, what seems to be inexplicable is that you are reading it anyway. So help make the world more understandable and quit reading this post. I mean now. No, really. It's pointless and time wasting, even to be typing this, and infinitely more so to be reading it. So I'm going now, for a cup of coffee. Hah! I'm back. And, what? You're still here? Still reading? Let me recommend Getting a Real Life 101, an introductory course being taught at my local community college. Sorry. That was sarcastic. Didn't mean it. You have a perfect right to waste your time. If that is even a possibility. There is a school of thought that puts forth that any human activity, even reading vacuous posts on puzzle sites has eternal consequences. Of course, there is no clue as to whether said consequences have existential import. Or any import. But perhaps the pursuit of that question in and of itself has existential import. I for one do not know the answer to that question. Nor do I have any plans to post it as a puzzle. Actually, I'm only making this post to find out whether I can attach a file to a post that is not for example a graphical image. I'm sure there may be philosophical approaches to determining this, but I am an engineer by training and an experimentalist by vocation. So I intend simply to attempt it and see what happens. There is the complication that I am a retired experimentalist, but I'm thinking that that really should not matter. The laws of physics surely did not observe my retirement, and things should be now as they were, prior to. I'm convinced of it, in fact, and I'm somewhat reassured by the likelihood that it is true. Although from another point of view it places the personal events of my life in a somewhat diminished light. It is saddening to a degree that they may have had no effect whatsoever on my world and might have generally gone unnoticed. All of this really doesn't matter however. And because of that, the question arises once more -- why are you reading this? And that answer would seem to open myriad questions about that overall state of affairs in your life. Not to question them, nor to cast even a hint of utter meaninglessness to them, for that would be unkind and presumptuous, neither or which is my purpose in writing the pointless post. Which I am once again getting around to. I'm going to go now, and attempt to attach my file. When I get back I expect you to be gone, and therefore will not write anything more.. APL Idioms.doc There. It's attached and soon will be posted. Glad to see you've gone. See if you can decipher a few hundred APL idioms. Or, go make a contribution to society. Anything. Just quit reading this ridiculous post. Your friend, bn.

Yes. Basically I'm wondering whether the number of sides of the containing (regular) polygon matters. I'm working on it, don't have the answer yet.

This answer is seen to apply for triangles covering the center of any containing shape that has four-fold rotational symmetry, including the circle, such as square and octagon. Does to hold for triangles contained by other shapes, say a pentagon?

Consider the next two numbers as a pair, rather than singly.

Great - that's the "orderly" connection the puzzle alludes to. 40 is not just the first, but the only, number with that property. Same with dos and ein, which I thought was interesting. That's the first part, and now the properties of the next two numbers are sure to follow.

For starters, think about just the first number. This is a good puzzle. Really.

My memory was faulty. Only the three fastest can be determined in seven heats.

It's in that range. Can you nail it down? See my post #6.