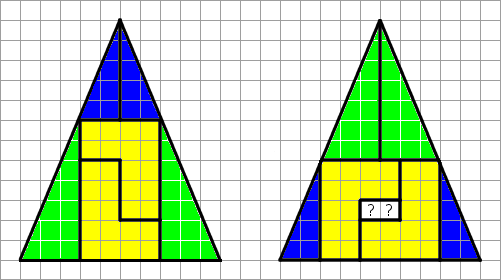
-
Posts
204 -
Joined
-
Last visited
-
Days Won
3
Content Type
Profiles
Forums
Events
Gallery
Blogs
Everything posted by jasen
-
Start from 2nd statement, It must be true, because it can't be the first false statement. If it the first false statement, it become liar paradox. So 1 False, 2 True, 9 False and 10 False.
-
Sorry, I think I made mistake, my computer search give me wrong number due to limitation of floating point number. So I still don't have the answer yet. But checking internet source, it is believed there is no such number. http://mathworld.wolfram.com/PentagonalSquareTriangularNumber.html
-
0 and 1 are a triangle number, a square number, and also a pentagonal number what is the next number (after 1) which is a triangle number, a square number, and also a pentagonal number ? clue : Surprisingly The number is more than 30 digit number.
-
I'm finding this interesting conjecture, maybe I'm not the first to state this conjecture. I have tested this conjecture to 100.000 first positive integer. anybody can provide the prove or disprove this conjecture ? the conjectre is : Every positive integer can be written as additon of 1 triangle number, 1 square number, and 1 pentagonal number note : Triangle numbers are generated by the formula, tn = ½n(n+1). The first ten Triangle numbers are: 0, 1, 3, 6, 10, 15, 21, 28, 36, 45, ... Square numbers are generated by the formula, Sn=n*n. The first tenSquare numbers are: 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100,... Pentagonal numbers are generated by the formula, Pn=n(3n-1)/2. The first ten pentagonal numbers are: 0, 1, 5, 12, 22, 35, 51, 70, 92, 117,... 100 first positive integer which follow the conjecture :
-
ignore this
-
If we change Thalia answer with ABC solution, than replacing ABC with permutation [2,3,5], we can get 6 diffrent answers, one of it is as picture bellow
-
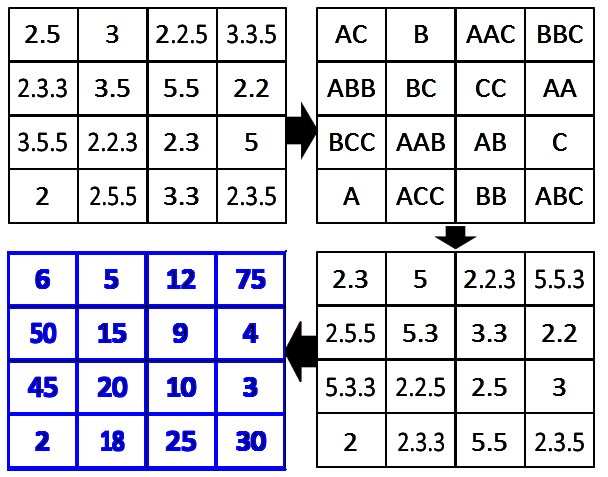
To attack the problem, first write the numbers into its prime factors 2 = 2, 3 = 3, 4 = 2.2, 5 = 5 6 = 2.3, 9 = 3.3, 10 = 2.5, 12 = 2.2.3 15 = 3.5, 18 = 2.3.3, 20 = 2.2.5, 25 = 5.5 30 = 2.3.5, 45 = 3.3.5, 50 = 2.5.5 75 = 3.5.5 So all numbers are consist of 3 prime seed 2,3 and 5 Now replace each seed with 3 symbols, A,B and C So what we get now is A, B,C,AA,BB,CC,AB,AC,BC,ABB,ACC,BAA,BCC,CAA,CBB, and ABC There are 12A,12B, and 12C Total symbols, so each line must have 3A,3B and 3C What we have to do now is Put A,B,C,AA,BB,CC,AB,AC,BC,ABB,ACC,BAA,BCC,CAA,CBB, and ABC to a 4x4 square table, so every horizontal, vertical and diagonal line have 3A,3B, and 3C.
-
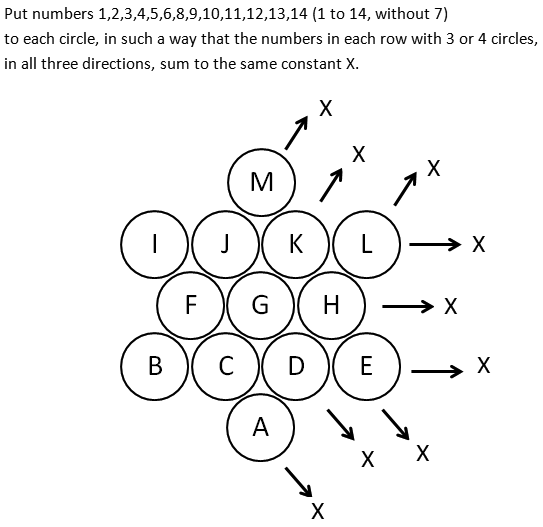
Put number 2,3,4,5,6,9,10,12,15,18,20,25,30,45,50 and 75 to a 4x4 square table, so the product of 4 squares at every horizontal, vertical and diagonal line are same.
-
We are 3 sisters, today our ages are primes, interestingly the difference of our ages are also primes. How old we are ?
-
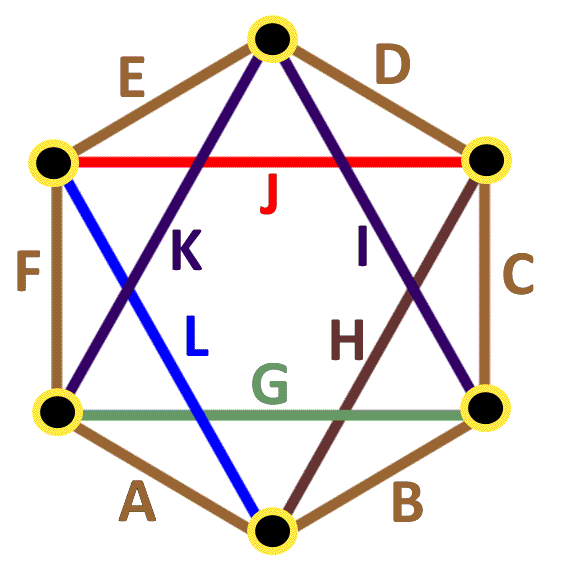
Put number 2,3,5,6,10,12,15,18,20,45,50, and 75 to each line in the picture, so the product of lines which meet in every dot are equal. A*L*H*B = B*G*I*C = C*H*J*D = D*I*K*E = E*J*L*F = F*K*G*A if rotation and reflection are considered as 1 same solution, There are 16 solutions.
-
At a math class, a teacher gives his students 4 numbers, lets say the numbers are A, B, C and D Then the teacher ask his students to make an equallity equation from the numbers. Claudy says 2*a*b = c + 2*b Leon says a*b*c = 12 * c Jemmy says b*b + c*c = (a+b)^2 Thomas says 30*d = 6*b*c Richard says a+b+c+d = a*a Then the teacher says "Ok students, you are smart, but one of you is wrong" If the numbers are positive integer not more than 100, Who is wrong, and what are the numbers ?
-
answer for 1st question is correct, but for 2nd question is wrong. 13 * 786 = 10218 , 31 * 786 = 24366
-
2 Silmilar Questions 1. Replace each letter (A to I) in equation bellow with number (1 to 9) to make them correct AB * CDE = CB * AED = FGHI 2. Replace each letter (A to I) in equation bellow with number (1 to 9) to make them correct AB * CDE = CE * ADB = FGHI
-
arrange the digits from 0 to 9 into a number so the number is divisible by 12 to 21. (there are 2 answers)
-
There is a number of kids in a stadium, the kids form 7 groups which each group contains equal number of kids. than 2 kids left the stadium, the remaining kids form 6 groups which each group contains equal number of kids. than 3 more kids left the stadium, the remaining kids form 5 groups which each group contains equal number of kids. than 5 more kids left the stadium, the remaining kids form 4 groups which each group contains equal number of kids. than 7 more kids left the stadium, the remaining kids form 3 groups which each group contains equal number of kids. If the initial number of kids is not more than 750 kids, how many kids in the stadium at the beginning ?
-
-
Bonanova, you are very close, your explaination is very cool, just quite not carefull. check again your exhaustive search list , you miss something.
-
Sum of sides means sum of all 12 sides, sum of surface area means sum of all 6 areas. Ignore the dimensions. Let say length in m, area in m2 and volume in m3 All length are integer.
-
I have a box Rasio of length, width and height of the box is a:b:c Rasio of sum of sides, sum of surface area and volume is also a:b:c find the length, width and height of the box a, b and c are integers & can be the same number.
-
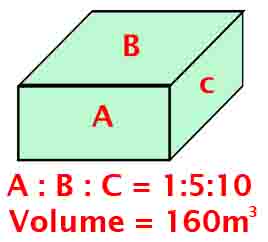
I know this math problem is easy for the master here, But it will be interesting for new members I have a box, rasio of the three surface area are 1:5:10 If the volume of the box is 160m^3 find the length, width and height of the box
-
-
-
sorry I'm wrong, ignore it