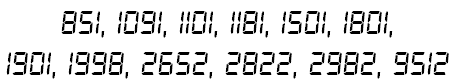-
Posts
204 -
Joined
-
Last visited
-
Days Won
3
Content Type
Profiles
Forums
Events
Gallery
Blogs
Everything posted by jasen
-

Arrange numbers and operators to the magic triangle
jasen replied to jasen's question in New Logic/Math Puzzles
When creating this puzzle (using computer), I started with 3 first constraints, then I got many solutions, so I have to add 1 more constraint. But I have to keep the symmetry of the puzzle. First I tried to sum the three corners, but I still got some solutions. Then I tried to product the three corners, which yields 1 unique solution. When creating this puzzle (using computer), I started with 3 first constraints, then I got many solutions, so I have to add 1 more constraint. But I have to keep the symmetry of the puzzle. First I tried to sum the three corners, but I still got some solutions. Then I tried to product the three corners, which yields 1 unique solution. -
based on this @bonanova puzzle, I create another similar puzzle You are given the following ten statements and are asked to determine a particular number. At least one of statements 7 and 8 is true. This either is the first true or the first false statement. The number is a prime number. The first true statement multiplied by the last false statement divides the number. The number of divisors of the number is greater than the sum of the numbers of the true statements. The number has exactly 4 prime divisors. The number is bigger than 1000. The numbers of true statements do not equal the numbers of false statement One of the divisors is a cube number bigger than 1. There are 3 consecutive False statements and 3 consecutive True statements.
-
yes there are still 2 more solution.
-

Arrange numbers and operators to the magic triangle
jasen replied to jasen's question in New Logic/Math Puzzles
Yes you are right, each operator only can be used once. making ((9!)(6!))/3 cases. (Because of the symmetry) -

Arrange numbers and operators to the magic triangle
jasen posted a question in New Logic/Math Puzzles
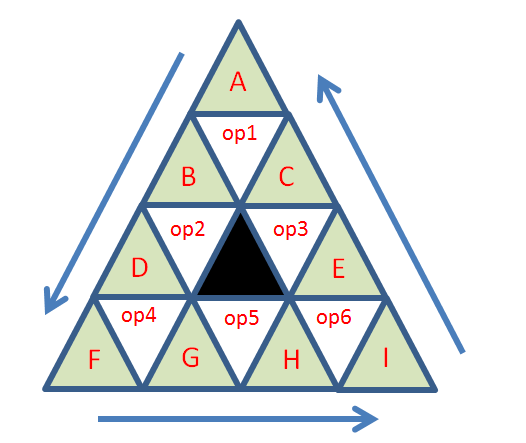
Note : A # B = A*10 + B Arrange the numbers 1 to 9 to green triangles, and arrange operator (+,-,x,/,^, and #) to the white triangles, so the math operations below are equals. (((A op1 B) op2 D) op4 F) = constant (((F op4 G) op5 H) op6 I) = constant (((I op6 E) op3 C) op1 A) = constant A x F x I = constant -

Reverse the order of 8 poisonous substances
jasen replied to jasen's question in New Logic/Math Puzzles
No, you can choose the robot in each step something like 2213232..... -

Interesting 3x3 table, to form a numbers of unique prime numbers
jasen replied to jasen's question in New Logic/Math Puzzles
-
8 very poisonous substances named s1 to s8 are kept in a safety room. The substances are kept in ascending order (s1,s2,s3,s4,s5,s6,s7 and s8). In the room there are 3 robots. First robot can "rotate left" the order of the substances. If the order is (a,b,c,d,e,f,g,h) the robot will make it (b,c,d,e,f,g,h,a) Second robot can split the substances into 2 part then reverse the order of each part. If the order is (a,b,c,d,e,f,g,h) the robot will make it (d,c,b,a,h,g,f,e) But the robot is a bit broken, so the resulting order is a bit wrong. The resulting order will become (d,c,a,b,h,g,f,e). Third robot can split the substances into 4 part then reverse the order of each part If the order is (a,b,c,d,e,f,g,h) the robot will make it (b,a,d,c,f,e,h,g) Questions If the 2nd robot is not broken, how many minimum step needed by using the robots to reverse the order into descending order? Show the steps! After the 2nd robot is broken, how many minimum step needed by using the robots to reverse the order into descending order? Show the steps!
-

Interesting 3x3 table, to form a numbers of unique prime numbers
jasen replied to jasen's question in New Logic/Math Puzzles
It is possible, I have it. I will show it next week if nobody find it until 10 Nov 2016. -

Interesting 3x3 table, to form a numbers of unique prime numbers
jasen posted a question in New Logic/Math Puzzles
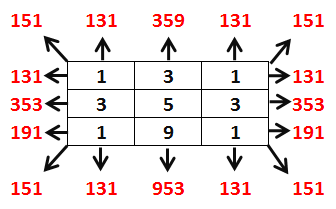
151 131 359 131 151 \ ^ ^ ^ / 131 < 1 3 1 > 131 353 < 3 5 3 > 353 191 < 1 9 1 > 191 / V V V \ 151 131 953 131 151 This 3x3 table have an interesting properties. Every direction (up,down, Right, Left, 45°,135°,225°,315°) of 3 cell form prime numbers. There are 6 unique prime numbers from this table, they are 131, 151, 191, 353, 359, 953. Create a more interesting 3x3 table with the same rule, which there are 9 unique prime numbers from the table. -
Example : a---b---c / \ / \ d e f g / \ / \ h---i---j---k---l \ / \ / m n o p \ / \ / q---r---s a+b+c = a+e+j = c+f+j = 23, and so on.... Note : There are 2 solutions, if we rule out reflections and rotations. Bonus Puzzle : How if all the rows of 3 numbers between O (big o) sums to 22,24,25,26,27,28,29,31,32,33,34,35,36, 37, and 38. I have checked all the solutions by computer, and all those sums have solutions.
-

Interesting pattern on 5x5 table which has unique properties
jasen posted a question in New Logic/Math Puzzles
[0,1,6,4,3] [4,5,6,0,9] [9,9,0,1,1] [1,0,4,5,6] [7,6,4,9,0] This 5x5 table has unique properties. Each number in a cell means : or Here is another example [0,1,6,4,8] [1,2,1,3,2] [1,0,9,0,1] [4,5,6,0,4] [4,5,1,0,9] [6,5,9,5,6] [4,4,0,6,6] [3,3,0,7,7] [5,5,0,5,5] [1,0,4,5,1] [1,0,9,5,6] [9,0,1,0,9] [2,1,4,4,0] [8,7,9,8,9] [4,5,1,5,4] What surprised me is, every table like this will follow this : I have checked this with my computer. Why this happens ? -
Solve this alphametic ENLIST + SILENT + LISTEN = ANAGRAM Leading zero is ok. There is only 1 solution.
-
Solve this alphametic (replacing letters with digits) ABCDEFG mod (A×B×C×D×E×F×G)=0 example : ABCDE mod (A×B×C×D×E)=0 13248 mod (1×3×2×4×8)=0 Note : Do not replace any letter with 0. Each letter represent different digit. There is only one solution.
-
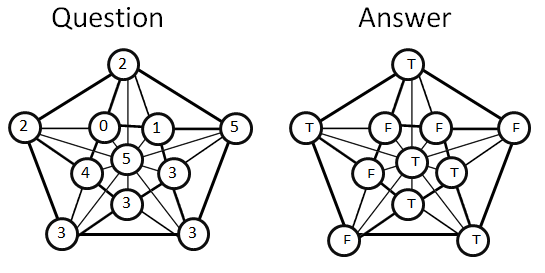
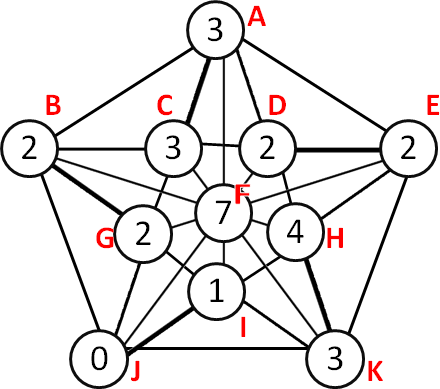
Let’s say a true circle is a circle with a true statement. So if the number is 3 means the circle is connected by 3 true circles. Some circles are true and some are not. Each circle is connected to 5 other circles, except the middle circle. The middle circle is connected to 10 other circles. Create another star with Boolean (T/F) input, to show which circles are true, and which circles are false. Example Note A is connected to (B,C,D,E,F)B is connected to (A,C,F,G,J)C is connected to (A,B,D,F,G)D is connected to (A,C,F,H,E)E is connected to (A,D,F,H,K)F is connected to (A,B,C,D,E,G,H,I,J,K)G is connected to (B,C,F,I,J)H is connected to (E,D,F,I,K)I is connected to (J,G,F,H,K)J is connected to (B,G,F,I,K)K is connected to (J,I,F,H,E)
-

Guessing right number from 1 to 27, with 3 Yes/No/Maybe questions.
jasen replied to jasen's question in New Logic/Math Puzzles
-

How many spin-able numbers are there from 0 to 99999 ?
jasen posted a question in New Logic/Math Puzzles
0,1,2,5,8,11,69,96 are spin-able numbers. We call a number is a spin-able number if : How many spin-able numbers are there from 0 to 99999 ? This is a no-computer puzzle, only right answers with explanation will be accepted. -
Your best friend (Bob) comes to you with this problem. The Problem His teacher (Mr. Sam) will ask Bob to work out a number in a child (Joan) head from 1 and 27. Bob has to find the correct number, by asking Joan three Yes/No questions about the number. Joan can respond with 3 different answers: "Yes", "No", or "I do not know". Joan is a smart boy, but he doesn't know about another base number except 10. So by asking that kind of question he will answer "I do not know" Example: If the number is 12 Is it an even number? Yes. Is it divisible by 9? No. If I take a random number between 10 to 15, will I get the right number? I do not know. ------------------ Another Example: If the number is 9 Is it an even number? No. Is it divisible by 9? Yes. If I take a random number between 10 to 15, will I get the right number? No. ------------------ Find the strategy, so every number from 1 to 27 can be guessed correctly.
-
@ bonanova If you mean same puzzle with different numbers, you can create It is easily, but maybe the solution is not unique. if you mean different puzzle with T/F statement, I do not have, but I wiil create it, with another shape, maybe hexagon, triangle, or etc.
-
1 3 2 3 1 3 3 2 3 3 2 2 3 3 2 3 3 3 4 4 1 3 2 4 1 This 5x5 table has unique properties. Each number (x) in a cell means : Example : (2,2) cell (red) is 3, so it is surrounded by 3 unique numbers (1,2 and 3) (4,4) cell (blue) is 4, so it is surrounded by 4 unique numbers (1,2, 3 and 4) The Question 3 . . . . . . . . 2 . . . . . 2 . . . . . . 3 . . Fill in the blanks so the table has the same unique properties.
-
@ Phill, to make the question clear, I will explain the example 1 3 -> T F 0 1 F T (1,1) is true because the cell, is surrounded by 1 true statement (2,2) (1,2) is false because the cell is not surrounded by 3 true statement, it only surrounded by 2 true statement (1,1) & (2,2) (2,1) is false because the cell is not surrounded by 0 true statement, it surrounded by 2 true statement (1,1) & (2,2) (2,2) is true because the cell, is surrounded by 1 true statement (1,1)
-
@bonanova : yes diagonals count.
-
Statement table. 3 2 1 4 1 2 3 3 3 3 3 4 6 4 4 2 3 4 4 3 1 1 2 4 3 Above 5x5 table contains numbers. A number at each cell represent a statement. So if the number is 3 means the cell is surrounded by 3 True statement We can say all statemets are false, but this is not what I want. Some statements are true and some are not. Create another 5x5 table with boolean (T/F) input, to show which statements are true, and which statements are false. example for 2x2 table. 1 3 -> T F 0 1 F T I have checked there is only 1 solution. Find the solution !