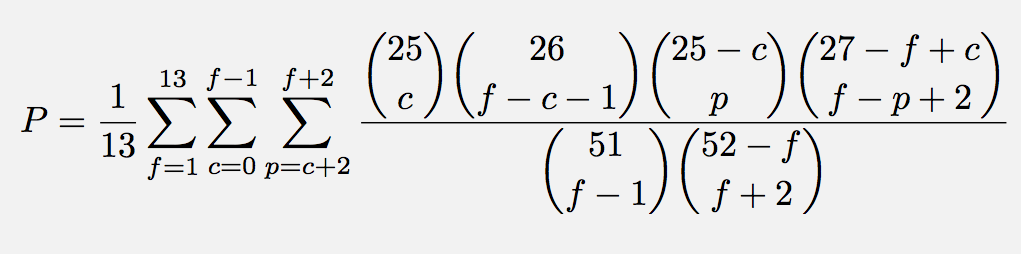bushindo
-
Posts
719 -
Joined
-
Last visited
-
Days Won
5
Content Type
Profiles
Forums
Events
Gallery
Blogs
Everything posted by bushindo
-
A simple (*not* bonanova 'simple') hat problem
bushindo replied to Yoruichi-san's question in New Logic/Math Puzzles
Ah, I see what you are getting at then. Your claim is absolutely right. This is a superbly designed puzzle, by the way. -
A simple (*not* bonanova 'simple') hat problem
bushindo replied to Yoruichi-san's question in New Logic/Math Puzzles
My impression of the claim you intend the BD to prove is the following: Claim: Given that the fishermen figure out a way to alert all the other players when they've figured out their hat, then the fishermen should be able to solve what color hat they are wearing through just logic; that is, they do not need to confer among themselves for a common strategy. In other words, let's say that we remove the fishlines from the problem, and just assume that there is a royal announcer. Every time participant X raises his hand, the royal announcer would then intone within all participant's hearing "Participant X is ready to guess his hat color". Are you saying that, without absolutely no talking among themselves before the game start, the 5 participants can logically come to a solution that is guaranteed to win? -
A simple (*not* bonanova 'simple') hat problem
bushindo replied to Yoruichi-san's question in New Logic/Math Puzzles
This is puzzling, since a previously-agreed-upon strategy is the hallmark of these everyone-must-be-correct-to-win problems. I would like some clarification. Do you mean to say "If there was no time to devise and agree on a strategy, hence allowing the fishermen only to raise their hand when they knew their own color of hat, what is the algorithm for the first fisherman such that the 5 participants are guaranteed to win?" Or perhaps you mean to ask for an algorithm for the first fisherman such that the chance of fishermen winning is as high as possible? -
A simple (*not* bonanova 'simple') hat problem
bushindo replied to Yoruichi-san's question in New Logic/Math Puzzles
Well, here's are some strategies Minor details about the fish lines
-
A simple (*not* bonanova 'simple') hat problem
bushindo replied to Yoruichi-san's question in New Logic/Math Puzzles
I would like some clarification. My impression is that whenever a participant raises his hand, the other 4 participant would be aware of this fact. For instance, if participant 1 raises his hand after the first gong sounding but before the second gong sounding, the other 4 participants would be aware that number 1 raised his hand, even though they would not know the color of 1's hat. Is this true? -
A really simple connect-the-dots problem
bushindo replied to bonanova's question in New Logic/Math Puzzles
Here's an attempt, -
This is indeed the correct probability. Congrats! (14.swapnil.14 made the same conjecture but made some mistake in the calculations). However, the solution to this puzzle is slightly incomplete (for me) because the probability computation relies on the unproven fact that There is a neat proof for this fact, and I think the fine denizens of the den would appreciate the challenge of working why the above statement is true. Instead of posting that fact as a new puzzle, I think I'll declare this puzzle to be half-solved, and revise the OP to include this new challenge.
-
Suppose that there is a thin, circular ring of wire with circumference of 10 meters, and that we have some ants with the following properties, 1) All the ants when placed on the wire will travel at a fixed, constant speed of 1 meter/minute in the direction that they are heading. 2) When any two ants collide on the wire, each ant will instantaneously turn around and travel in the opposite direction at the same speed. Suppose that we simultaneously place 14 ants at random locations on the ring. The orientation in which each ant is headed (clockwise or counter-clockwise) is determined by a fair, random coin flip. 13 of the ants are colored black, and 1 of the ants is colored red. We let the ants run around the ring as specified by the conditions above. After precisely 10 minutes, what is the exact probability that the red ant will end up at the spot it started in the beginning of the game? Extra bonus:
-
First of all, let me say that this is an excellent problem. Thanks for sharing it.
-
The full expression for the chance of beating Vern at this game is
-
Here's a non-calculus guess
-
You didn't read the choices incorrectly. I was just being faceticious :-). Please carry on.
-
This is an easy one
-
Thanks for the problem. By the way, congrats on the 1000th post.
-
Thanks for sharing these little gems with us, superprimastic. I enjoy the journey greatly, and feel enriched by the experience. Also, thanks for you recommendation. I picked up the Stanford Mathematics Problem Book for my ereader, and look forward to spending some time on it.
-
Let me just chime in and say that I like your puzzles as well. I'm always happy to see new topics that you post. Can you recommend one or two of these expository texts? There are some time slots in my life that I'd like to put to better use.
-
I would like some clarification. What do you mean by 'thinking of the numbers in their binary representations'? My interpretation is that nCk is odd if and only if n = k and k > 0, but that interpretation is clearly false. Clarification would be appreciated. Thanks.
-
This is such an elegant problem. I'm amazed at how the algebra works out nicely. Thanks
-
Clear and elegant as well. Good job!
-
Thanks superprismatic and witzar. That is really a silly oversight in the wording of the puzzle. The intent is to show that under certain starting lamp patterns, there is a strategy which will guarantee that the butler will never be able to turn all the lights on. I'll fix it in the OP. Thanks for pointing that out.
-
Let's say that you are setting the dining table for a party of 60 guests. The 60 guests will be seated at a giant circular table. Each seat has a lamp, and currently some of the 60 lamps are on and some are off. The butler offers to play a game with you. Let's say that the chairs are labelled with the guests names, which for convenience we label starting from the top and going clockwise as C1, C2, ..., C60, and the chairs are stationary. The giant circular dining table along with the lamps, however, can rotate. Each lamp has a switch, and flipping the switch when the lamp is on turns it off, and vice versa. The game is as follows 1) The game consist of turns. At each turn, the butler tells you a list of chairs at which he want to switch the lamps' state. 2) You will then has the option of arbitrarily rotating the entire table before applying the switches at the list of chairs in point 1). Please note that the you must rotate the table in such a way that each chair is directly across from a lamp (rotating so that a lamp ends up midway between two chairs isn't allowed). You can turn the table in any direction and for as many spaces as you want before applying the switches. 3) You may take as many turns as you'd like. If the butler succeeds in turning all the lights on, he wins. Show that under certain starting lamp patterns, there is a strategy which guarantees that the butler will never be able to turn all the lights on. EDIT: added the proper initial constraints thanks to superprimastic and witzar.
-
That's brilliant, witzar. Good work!
-
-
Some thoughts, mostly 90% hand waving and 10% proof by exhaustion
-
Adding the proof to complete the puzzle. Please excuse the formatting; typing a proof in the brainden editor is quite complicated.
