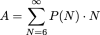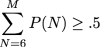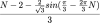-
Posts
719 -
Joined
-
Last visited
-
Days Won
5
Content Type
Profiles
Forums
Events
Gallery
Blogs
Everything posted by bushindo
-
There are many cases on purpose. The reasoning should be straight forward with the proper tools and elimination procedure.
-
This is based on bonanova's puzzle Here's a game that goes as in the following * There is a host with 14 stamps, 7 red and 7 blue. There are five players- A, B, C, D, and E. * In the beginning, the host affixes two stamps to each of the 5 players' head. The remaining 4 stamps go into the host's pocket. Each player can see the stamps on the remaining 4 players, but can not see his own stamps nor the four in the host's pocket. * Starting from A to E (and then looping back to A and so on), the host asks if each player definitively knows his stamps distribution (RR, BB, or RB). If the player does not know, the host goes on to the next player. No guessing is allowed. * The game goes as follows 1st turn- player A: I do not know 2nd turn- player B: I do not know 3rd turn- player C: I do not know 4th turn- player D: I do not know 5th turn- player E: I do not know Host- Alright, to help you, I'll now reveal two stamps from my pocket. *At this point, the host pulls out two of the four stamps in his pocket and shows everyone. The game then continues as before* 6th turn- Player A: I do not know. … Question- what is the longest possible number of turns required before a player definitely knows his color?
-
As stated in the OP any audience member who is not a truth-teller or a liar will randomly lie or tell the truth. If you like, s/he could make that decision by coin flip. Clarifications, please 1) Does each member of the audience know the type of all remaining audience member? 2) For the audience members that randomly tell the truth or lie, at any moment, do they know whether they will lie or tell the truth to the next question? That is, before hearing a particular question, have they already decided on lying or telling the truth?
-

Staying alive with an eight-sided die
bushindo replied to bonanova's question in New Logic/Math Puzzles
Good solve, CaptainEd. Nice and compact solution =) -

Staying alive with an eight-sided die
bushindo replied to bonanova's question in New Logic/Math Puzzles
Here's an approach -
My guess
-
Here's a winning strategy In this example, doesn't 2nd player win on his 3rd move having (2,7,6)? Shucks, back to the drawing board.
-

Closed form expression on steroids
bushindo replied to bushindo's question in New Logic/Math Puzzles
Excellent answer -
Here's a winning strategy
-

Closed form expression on steroids
bushindo replied to bushindo's question in New Logic/Math Puzzles
Comments -
This is based on a previous Find a closed form expression for function f(N) such that f( N ) = 0 for 1 <= N <= 11 f( N ) = 1 for 12 <= N <= 22 f( N ) = 2 for 23 <= N <= 33 f( N ) = 3 for 34 <= N <= 44 f( N ) = 4 for 45 <= N <= 55 ... No modulus or rounding operators are allowed.
-
I agree with the note about median. I think the problem here is that the OP and post 14 (see blue-colored part in spoiler above) are conflating the median and the average (or mean) in the interpretation of the winning condition
-

Can you find a closed form equation for the sequence?
bushindo replied to Rob_Gandy's question in New Logic/Math Puzzles
-
This is great - beautiful, even.Except, the power tower unfortunately does not converge for both cases (for 2, but alas not for 4 as I remember.) I made a graph of the divergence point sometime back, I will look for it. When the records are written, however, this def gets Honorable Mention. Great proof as well. I have no beef with the power tower, but isn't the argument similar to this one
-
If only a binary signaling scheme is allowed, CaptainEd has shown that only prisoner 1 needs to change his mind. Even in the stricter NS view, there are some latitude to define a quadnary signaling scheme due to an implied necessary condition
-
Counter example to this proof =)
-
How about this *very easy and straight forward* method?
-
Continuing with the community solve approach, can we clarify: Must all the persons in a particular row face the same direction? If prisoners in say the Yellow row can face in differing directions does that constitute [illegal] communication? Can the first two prisoners choose the time that they [legally] alter their position, at any time up to the last prisoner takes his place? During making raws...some of them can be..back to back (in any raw)...but by reaching the last prisoner,they all shoud be at the same direction But only the first two prisoners can move. This means the seventh prisoner, say can come into a row back to back with someone else in that row, then at a later time switch his direction so that at the end all in that row have the same direction. So as long as a prisoner stays in the same position, he can flip his direction back and forth during the formation of rows. That sounds like communication. Another piece of jello fell off the nail... Yes....in my OP I said....each prisoner should choose his raw and once he did,he is not allowed to change his mind,but turning around himself was not mentioned This seems to imply that turning around (spinning or rotating) is allowed, even though switching rows isn't allowed. Isn't that a contradiction of the requirement of the OP, which I list below Communication is defined as 'the imparting or exchanging of information or news', so by any reasonable interpretation, turning-in-place is considered a violation of the rules. If communication is allowed, then the puzzle becomes trivial. In fact, we don't even need to allow the first 2 prisoners to change their minds if we allow them to communicate.
-
Here is the recursive code I used. The logic behind it is already described by Prime's excellent and insightful analysis.
-
With some recursive code, I get
-
-
Forgot about some cases in computation of winning chance. Back to the drawing board.
-
The problem is skillfully analyzed and solved by k-man and bonanova. Kudos, everyone. Yes, the Monty Hall reference was meant as a red herring, but apparently that false clue isn't enough around these parts.
-
Here's a twist on the Monty Hall problem. Some of you might be familiar with a show called Deal or No Deal. For those you are not familiar, a simplified version of the show is as follows, * There is a host, a player, and 40 suitcases of money. * The host informs the player that there are 39 empty suitcases and 1 case with 1 million dollars. The suitcases are closed and the player has no idea how much each specific suitcase contains. At the beginning of the game, the player is requested to choose 1 suitcase at random. Let's call this the Chosen Suitcase * At the beginning of each turn, the player is requested to choose 1 suitcase from the remaining Non-Chosen Suitcases, reveal the contents, and put this case and contents in a discarded pile. After this, the player has the choice of quitting the game and keep the content of his unopened Chosen suitcase, or switching his Chosen Case for one of the remaining Non-Chosen Cases and play on. Let's say that the player goes through 38 turns, opening and discarding suitcases without ever switching his original Chosen Case. The 38 opened cases are all empty. There are now only 2 unopened cases left, and 1 of them is currently chosen by the player. Should he switch his original Chosen Case for the remaining Suitcase for the best chance to win 1 million dollars? Assuming optimal strategy, what is the player's probability of winning the 1 million dollars in this situation?