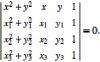bonanova

It's also the probability that a "2" is present ... and so on. It's not a surprising result, once one realizes that most natural numbers are greater than Graham's number.

I played with this puzzle, or one very much like it, back when I first joined Brainden, back in 2007. I have some of the figures I drew for it, but I can't locate the posts. So I can't reconstruct the solution. What I do recall was the answer was surprising and difficult to see even when given. I also can't locate the source I had. Thinking it was one of Martin Gardner's books, but it eludes my present search. I'll watch this one being solved here again.

The number of apples in rooms 1 and 2 are described by the same words. What if Bob had gone to Room 2 first? Or is that the flaw?

Are all the natural numbers written on slips of paper and put into a hat?

how would one construct this?

Ÿes. And yes ... you did say weld, didn't you? Back to the drawing board.

Wow thanks k-man. Since it's very unlikely that 0/8 or 8/0 cases exist, 6/2 with p(obtuse) = 3/4 looks like the highest case, with a smattering of lower cases dragging the overall average down a bit. This gives great credence to plasmid's simulations, and probably puts this puzzle to bed. I'm looking at an approach that WOLOG places A on a radius at 12:00 (r, 0) where 0<r<1 and calculates plasmid's red and blue areas (from a few posts back) that lie inside the selection circle for a given B. Averaging or integrating over all B locations in the selection circle will then give the answer. If analytical expressions for red and blue areas can be found, then integration gives an exact answer (but that looks hard.) else, numerically calculating and averaging red and blue for B on a grid of points will give an approximate answer that can be refined by tightening the grid. But that looks hard also. This has been an interesting problem. I'm going to give it my rating point.

@plas Thanks for the expl -- I was grasping at straws. Your ABCA'B'C' example where acute=obtuse=4 has me thinking: I think those cases are few, I think the acute=2 obtuse=6 cases are plenteous, and I don't think other cases are possible. If that mix is representative, it can be consistent with the simulated 72%. It's intuitive to me that a square could be slightly more accommodating of obtuse triangles. I can't seem to get my old simulation computer (Vista) fixed. I might get sufficiently motivated by problems like this to learn Perl. @karthickgururaj, probably good to check rand, but I wouldn't have expected deviations at that level to produce a systematic bias in the result. This check should put the worry to bed for other simulations..

@koren, follow-up: a straightforward calculation shows p(obtuse) = 3/4 for random point triplets taken from the perimeter. If including interior points made p(obtuse) jump discontinuously to 1/2, it would be a tremendously interesting result. Don't you agree?

Wow. Good catch. I wish my simulation computer were running. I would love to play more with this. I haven't found any reputable (e.g. Wolfram) derivations of this probability. There are several derivations for 75% if the points are on (not inside) the circle. That is, for three random points on the circumference, p(acute) = .25; p(obtuse) = .75. Edit: This construction makes pairs of triangles (e.g. ABC and A'B'C') that are congruent. So of the 8 triangles, exactly 0, 2, 4, 6, or 8 are acute with the others being obtuse. I thought the distribution in every case was 6/2 (obtuse/acute). You show a 4/4 case. I wonder whether it's ever 8/0. Or 2/6.

Does this line of code for UnitCircle while (Math.sqrt(x[i]*x[i] + y[i]*y[i]) > 1); use the square corners, or ignore them?

@koren, your triangle generator is different from picking three points, and that is why your answer differs from results posted here by others. You may be familiar with the Bertrand paradox, in which "random" chords lead to at least three different results, or you may not. If an uncertain definition of "random" is something you've not thought of, you might Google "Bertrand paradox" and enjoy a really mind bending example of it. Sometimes running a simulation is a convenient way to confirm a particular calculated or constructed result. Writing a program forces one to obey the constraints of the OP and think carefully through the analysis. There is an interesting irony in the fact that while your post does not answer to the conditions of the OP, its tone does answer somewhat to its title. You will find that most people here try quite hard to pay attention. In the process, we all learn things from time to time.

The procedure can only be done for finite area. Remember AB was mapped to (0,0)(1,0). If we start with an infinite selection circle, then with probability 1 AB is infinite -- precluding the drawing of red and blue stuff. In all cases we first get a result for a finite-r selection circle then get to the plane by extending r to infinity. You can simulate the unit circle exactly in Perl. Just ignore selected points for which x2+y2>1. The result should be 75%

@plas, The procedure loses track of some constraints on C. ABC originate from a circle. AB is found to be the largest segment. Red and blue areas are then constructed on AB. C is then allowed to roam over the colored areas. In 64% of those cases the triangle is obtuse. In the picture of red and blue areas (3), the selection circle (1) is not shown. For some AB, parts of the colored area can lie outside the selection circle. The more likely color to lie outside is red, since the blue area is more central. Reducing red relative to blue increases the obtuse percentage. If this effect is averaged over all cases of AB, 64% might well converge to 75%. Take an extreme example where AB is a diameter of the selection circle. In this case the available red area vanishes, increasing the obtuse probability to 100%.

Given that both random points lie at infinity and cannot be compared, the argument of symmetry that holds on any finite portion of the real axis can be taken to hold in the infinite case. P[b<A] = 0.5

Assuming yes to both questions:

My take: [spoiler='Quick and dirty answer for finite circle']Place any three points A B and C in a unit (or any finite radius) circle. We prohibit ABC from all lying on a straight line. This is OK, because such configurations constitute 0% of all cases. Construct the points A' B' and C' so that the centers of the line segments AA', BB' and CC' lie on the origin. Inspect the eight triangles ABC, A'BC, AB'C, ABC', A'B'C, A'BC', AB'C' and A'B'C'. In every case exactly six of the eight triangles are obtuse. The probability of an obtuse triangle in a finite circle is 0.75. --------- If the OP has a solution, it is the same as for a circle of finite radius.

Does the greatest angle (of triangles constructed from three random points) actually have a uniform distribution over the range [60o, 180o]? I can't think of an immediate proof. That doesn't mean there is no proof. But perhaps it is the case. And it does lead to (what I believe is) the correct answer. Nice approach!

I suggest, we construct a kind of "triangles generator": We take a circle of any diameter, draw a chord AC from the endpoints of the chord we draw two line segments, the ends of which intersect on the circle. Symmetrically we draw two other segments on the other side of the chord and we got two triangles. When the chord is coincides with diameter the triangles are identical. The final touch – we connect the vertices of the triangles by line a-a. "Triangles generator" is ready let's start generate. For this purpose we are doing two things: 1) Moving the chord parallel to itself from the diameter stepwise with any resolution you choose. 2) At each step we move the line a-a together with the vertices of the triangles from point B to point A. By action 1 we iterate through all possible angles at the vertices of the triangles. (Look at nice animation here) By action 2 - iterate through all possible conjugate base angles. Eventually we generate all possible variants of triangles. At the resolution tending to zero we get close to infinite number of triangles, but an interesting observation for us, that in any case each specific obtuse triangle always has one corresponding acute-angled triangle. In other words: THE PROBABILITY OBTAIN OBTUSE TRIANGLE AT RANDOM CHOICE IS 50%. One must be careful when defining random triangles. There are many ways, yielding various distributions. The OP requires a particular method: selecting three points at random. This is easily done (for the unit circle) by selecting x and y values in the closed interval [-1, 1] and discarding any points for which x2+ y2>1. Inspecting a million or so triangles constructed from triplets of such points gives a clear answer to the probability in a finite region.