-
Posts
6975 -
Joined
-
Last visited
-
Days Won
66
Content Type
Profiles
Forums
Events
Gallery
Blogs
Everything posted by bonanova
-
Under the same conditions, then, it's trivial to make a 2, using just a 5 and a 2?
-
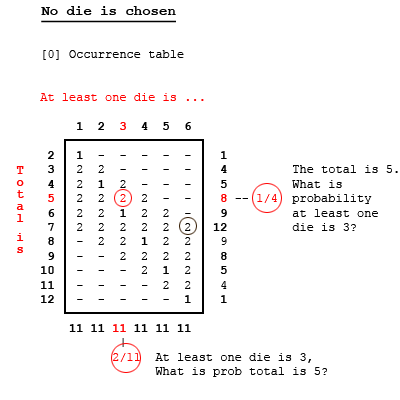
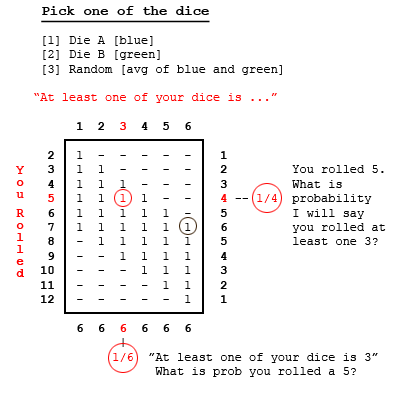
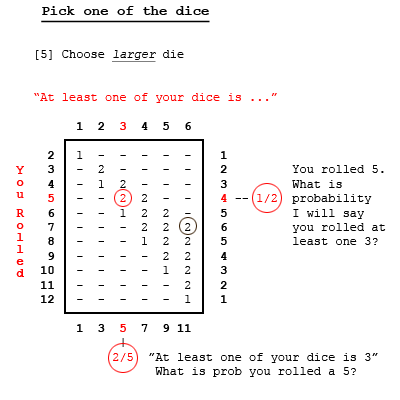
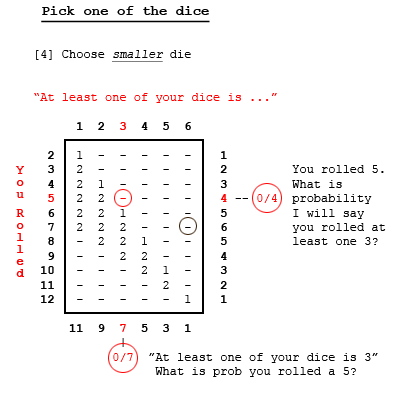
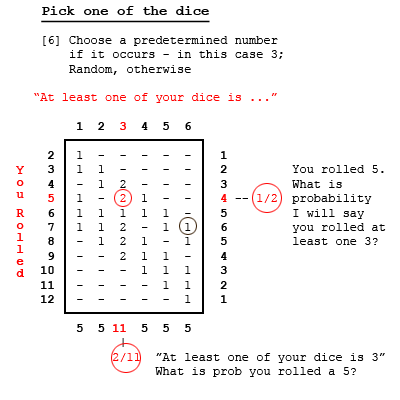
Let's see if we can tidy up here. Make a table of outcomes [dice total] when at least one die is 1. There is one outcome [1-1] that makes 2; two outcomes [1-2 and 2-1] that make 3; and two more outcomes each for totals of 4, 5, and 6 -- a total of eleven. Complete the exercise for die values of 2, 3, 4, 5, 6. Note there are eleven outcomes for each - a total of 66 in all; not 36, because we count occurrences of two numbers twice; doubles are counted only once. At this point, we are not choosing a die value to talk about. Just sorting out the occurrences for each value. Note some entries are blank. There is no way we can have a total of 2, for example, if one of the dice is 2 [or higher]. We can answer some questions immediately from this table. Look at the circled value of 2 in the "3" column and the "5" row. There are 11 outcomes in the "3" column. The circled 2 tells us when at least one of the dice is 2, the probability of the total of the two dice being 5 is 2/11 -- 2 occurrences out of 11. There are 8 outcomes in the "5" row. Now the circled 2 tells us when the total of the two dice is 5, the probability of at least one die being a 3 is 1/4 -- 2 occurrences out of 8. Finally, look at the gray circled 2 in the "6" column. That's our old friend telling us that if one or both dice is 6, the probability of the total being 7 is 2/11. It will be instructive to notice how the probabilities for the red circle [3 and 5] and the gray circle [6 and 7] change throughout this post. Now let's choose one of the dice by some means. To help matters, let's color them. Let's dye die A blue and dye die B green. Now we can distinguish them. Let Method 1 for choosing one of the dice be to choose die A - the blue one. We suspect the results will be the same for Method 2 - choosing die B - the green one. If they are the same, then Method 3 - a random choice say the average of A and B - will be the same, as well. Filling in the columns, as in the first case we ask how many ways can the first die be 1 and get 2 total - just one [1-1]. How many ways can we have a total of 3 if the first die [or 2nd die] is 1? Now the answer is just one: [1-2] and [2-1], respectively. And for a random selection of these cases, just one of them will be picked. Similarly for all the other entries. By choosing just one number from each roll, we count each of the 36 outcomes only once. Using one of the three methods mentioned, one of the dice is seen to be say, a three. Notice the probability of a 3 if the total is 5 is still 1/4, but the probability of rolling 5 given at least one 3 is now 1/6. Note also the probability of rolling 7 given at least one 6 is also 1/6. It's tempting to think that whenever we pick just one die, all the probabilities are such as they are here. This turns out not to be the case. Suppose we adopt Method 4 - picking the smaller of the two numbers. Or Method 5 - choosing the higher. Still choosing just one of the dice, the probabilities are changed. [edit] Note that since these are exclusive and exhaustive cases, they average to the random Method [3] - Add them up and divide by two. [/edit] In particular, note that if we choose the higher ranking die, the probability of rolling 7 of at least one of the dice shows 6, is our old nemesis 2/11. In the OP, if the magician was using Method 5, and if the first subject suspected as much [how, we could only guess], then his answer of 2/11 is the correct one. But that doesn't help much. The table shows that Method 5 tells Subject #2 ["one of your dice is 5"] to say 2/9, not 2/11. Well then. We ask, is there a consistent algorithm the magician might have used so that all six of the 2/11 answers were correct? It turns out there is, although the Subjects would have to have been psychic to find it. It's Method 6: Predetermine a number, and call it out if it's showing on one of the dice. And if not, then choose randomly from the two numbers that are showing. The final table shows Method 6 when the predetermined number is 3: If a 3 is showing, and if the magician predetermined he would call it if so, then the probability of rolling a 7 is in fact 2/11. You can read that from the table, where the 7 and 3 intersect, even though that 2 is not circled. What is the likelihood of this happening? The magician would have to have predetermined 6, 5, 4, 3, 2, 1 in that order. The subjects would have to have guessed that was his strategy. Each of the predetermined numbers would have to have shown in the dice that were rolled. No one would make money betting all of that would happen. But let's suppose it did: to accept the OP, where the magician complimented each for divining a correct response, it must have happened. The relevant probabilities are not fixed. They're neither 1/6 in all cases nor 2/11 in all cases. They depend on the choice Method; so we must assume a Method that makes OP consistent. And, unlikely as it is, we've found it. So finally we're left with accepting or disproving the argument by Subject #7 that ... for reasons noted in OP ... his unconstrained probability of rolling 7 must be 2/11. Well we've seen the [isolated and improbable] conditions for a 2/11 result, and Subject 7 didn't mention any of them, so we don't believe the argument. But to disprove it, we have to point out a fallacy. And there's one that is fairly obvious. For the first six subjects' answers to have been correct, as we've just seen, the choosing method [i.e. the value of the predetermined number] would have to be different in each case. Thus the six outcomes are not exclusive and exhaustive cases: they are "apples and oranges." Therefore they can't be combined, as Subject 7 reasoned they could. Thus the paradox is explained.
-
Oops. Thanks LIS Thread locked.
-
There could be many more, I’m sure. That of course is clear use of prepositions as examples of words, making them nouns: the name of a person, place or thing. Ah.. but OP said that was OK. Since this is a dead discussion, I'll not put this one into a spoiler. I read it a while ago and smiled: The Guinness Book of (World) Records used to have a category for "most prepositions at end". The incumbent record was a sentence put into the mouth of a boy who didn't want to be read excerpts from a book about Australia as a bedtime story: "What did you bring that book that I don't want to be read to from out of about 'Down Under' up for?" Mark Brader (msb@sq.com -- all this is to the best of his recollection; he didn't save the letter, and doesn't have access to the British editions) wrote to Guinness, asking: "What did you say that the sentence with the most prepositions at the end was 'What did you bring that book that I don't want to be read to from out of about "Down Under" up for?' for? The preceding sentence has one more." Norris McWhirter replied, promising to include this improvement in the next British edition; but actually it seems that Guinness, no doubt eventually realizing that this could be done recursively, dropped the category.
-
Allowing for variances in language fluency, the OP probably means to ask what number maximizes your chance of getting the job.
-
Nice! BTW, the triangle does not have to be acute, just neater that way. Can you imagine a philosophical thought consistent with these facts and the flavor text?
-
Start with all the deals
-
The moderator wipes a real tear from his eye as the denizens shake hands. Observation: formulas are conclusions without context - easy to use, impossible to refute. It's the context that is appropriate or refutable. Use with skill and care. Happy New Year guys.
-
Honorable Mention to reaymond for silliness AND creativity!
-
-
Linespersons at tennis matches call a service fault when a ball lands on the wrong side of a boundary line. Each person watches one line, and calls "long" or "wide" as appropriate Is it possible for a service fault to be missed using this approach?
-
A 1-acre field in the shape of a right triangle has posts at the middle of each side, with ropes just long enough to reach the two nearest corners. Sheep are tethered to the posts on the two sides, of length x and y respectively, and a dog is tethered on the hypotenuse. How many acres of grazing area outside the field do the sheep have to themselves? 0 acres - the dog can get to it all 1 acre 2 acres None of the above Can't tell without knowing x and y.
-
If rearrangement of the pieces between cuts in not permitted, a cube can be cut into 27 cubes by slicing twice in each of three perpendicular planes. By permitting rearrangement of the pieces, [slicing and stacking], can this be done with fewer than 6 cuts?
-

Hats on a death row!! One of my favorites puzzles!
bonanova replied to roolstar's question in New Logic/Math Puzzles
Hi gelfish and welcome to the Den. The puzzle states that thin events you mention won't happen. All the hats are in place before the prisoners speak, and it's implied they won't change afterward. -
With these I believe everyone agrees: Of all the couples with two children, at least one of which is a girl, equal numbers have, naming the older child first, {girl boy}, {boy girl}, {girl girl}. Of all the people who have rolled two fair dice, at least one of which is a six, equal numbers obtained, naming the dice in the order they came to rest say, {1 6}, {2 6}, {3 6}, {4 6}, {5 6}, {6 6}, {6 5}, {6 4}, {6 3}, {6 2}, {6 1}. If not, identify an unequal class. If so, treat them as axioms. Note the statements deal with populations, and they do not mention how we know [at least one girl] or [at least one six]
-
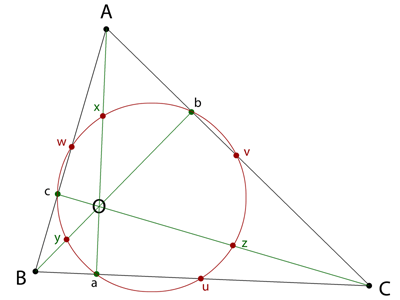
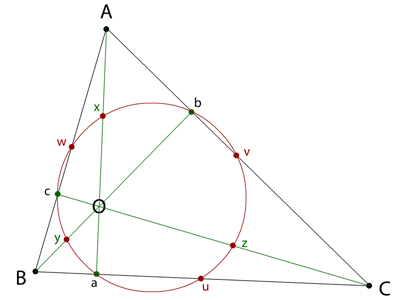
Nicely put. Yes, actually we know that all 9 points a, b, c, u, v, w, x, y, z lie on a circle. We used a, b, c to find the circle. The circle then found six other points related to the triangle. What are the six points [u-z]?
-
Or are you just trying to say that women are two dimensional - but still pretty creatures of note edit: do not know the book - btw What is/are notable about the six points u,v,w,x,y,z?
-
In Edward Abbott's charming book Flatland, women are needles [2-sided polygons] and men have 3 or more sides, whose number increased with nobility. Not surprisingly, circles are priests [infinite nobility]. Clearly the book was written before the age of political correctness. Although the circular priest differs greatly from the lowly triangular man, a simple geometric construction shows they nevertheless have six degrees: not of separation, but of commonality: Draw an acute [but not regular] triangle and the three lines that represent its altitude. That means using each of the sides, in turn, as the base. The points [a, b, c] where bases and altitudes intersect define a circle. The circle intersects each of the six lines: the sides (again), at [u, v, w], and the altitudes, at [x, y, z]. What is special about the six points [u, v, w; x, y, z] the priest and man have in common?
-
When I think of increased chances [probabilities] I tend to think it's because the favorable cases increased. Here, that isn't what happens - the total cases shrink a lot [all the at least one ace cases, where the ace is not ace of hearts] The favorable cases shrink, too, but not proportionately as much. So the probability increases.