bonanova Posted November 20, 2014 Report Share Posted November 20, 2014 (edited) The figure shows nineteen circles arranged hexagonally in fifteen rows of length 3, 4 or 5. Place consecutive numbers in the circles so that . At least one row in each of the three directions contains exactly one pair of numbers (e.g. 17 and 34) that differ by a factor of 2. Exactly one of the six outer vertices contains a prime. (1 is not prime.) Exactly one two of the six inner vertices (connected to the center) contains a prime. The fifteen row sums are identical. Edited December 7, 2014 by bonanova Correcting Clue 3. Quote Link to comment Share on other sites More sharing options...
0 k-man Posted November 20, 2014 Report Share Posted November 20, 2014 Can you clarify "consecutive numbers"? Does the puzzle require that all neighboring circles of a given circle had a number either 1 smaller or 1 greater than the number in the given circle? Or does it simply mean that the entire set of numbers used to fill in the puzzle must be a consecutive set? Quote Link to comment Share on other sites More sharing options...
0 bonanova Posted November 20, 2014 Author Report Share Posted November 20, 2014 Entire set. The numbers are consecutive, and they're placed on the grid. Same for 'Magic squares, sort of' puzzle Quote Link to comment Share on other sites More sharing options...
0 bonanova Posted November 30, 2014 Author Report Share Posted November 30, 2014 One of the numbers is 1. Quote Link to comment Share on other sites More sharing options...
0 DejMar Posted December 6, 2014 Report Share Posted December 6, 2014 (edited) There is a published paper that demonstrates that there is a unique solution to the order-3 magic hexagon.http://www.yau-awards.org/English/N/N92-Research%20into%20the%20Order%203%20Magic%20Hexagon.pdf ------ 3--17--18------ Condition 1 is satisfied with (4,8) in the fourth horizontal row, ----19-- 7-- 1--11---- and (2,4) in the second L-to-R-diagonal row. --16-- 2-- 5-- 6-- 9-- Condition 2 is sastisfied {3,9,10,15,16,18} only 3 is prime. ----12-- 4-- 8--14---- Condition 3 fails {1,2,4,6,7,8} both 2 and 7 are prime. ------10--13--15------Condition 4 is satisfied - all fifteen rows sum to 38. Edited December 6, 2014 by DejMar Quote Link to comment Share on other sites More sharing options...
0 gavinksong Posted December 6, 2014 Report Share Posted December 6, 2014 (edited) There is a published paper that demonstrates that there is a unique solution to the order-3 magic hexagon.http://www.yau-awards.org/English/N/N92-Research%20into%20the%20Order%203%20Magic%20Hexagon.pdf ------ 3--17--18------ Condition 1 is satisfied with (4,8) in the fourth horizontal row, ----19-- 7-- 1--11---- and (2,4) in the second L-to-R-diagonal row. --16-- 2-- 5-- 6-- 9-- Condition 2 is sastisfied {3,9,10,15,16,18} only 3 is prime. ----12-- 4-- 8--14---- Condition 3 fails {1,2,4,6,7,8} both 2 and 7 are prime. ------10--13--15------Condition 4 is satisfied - all fifteen rows sum to 38. Edit: I'm dumb. Edited December 6, 2014 by gavinksong Quote Link to comment Share on other sites More sharing options...
0 gavinksong Posted December 6, 2014 Report Share Posted December 6, 2014 Are we allowed to use negative numbers? And if we are, how does primality work? Quote Link to comment Share on other sites More sharing options...
0 DejMar Posted December 7, 2014 Report Share Posted December 7, 2014 Are we allowed to use negative numbers? And if we are, how does primality work? Primality only applies to positive integers (i.e., natural numbers) by definition. Yet, in a non-formal definition of a prime number, the negative of a positive prime number can be associated as being the same prime number. Thus, with the second definition permitting negative values, 2 and -2, for example, are the same prime, while by the first definition negative numbers are not prime. Quote Link to comment Share on other sites More sharing options...
0 bonanova Posted December 7, 2014 Author Report Share Posted December 7, 2014 DejMar has it. The puzzle has no solution for the clues as given, which contain an error in clue 3. My bad; there is one even prime number. Nice solve. Quote Link to comment Share on other sites More sharing options...
Question
bonanova
The figure shows nineteen circles arranged hexagonally in fifteen rows of length 3, 4 or 5.
Place consecutive numbers in the circles so that .
(e.g. 17 and 34) that differ by a factor of 2.
onetwo of the six inner vertices (connected to the center) containsa prime.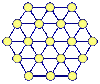
Edited by bonanovaCorrecting Clue 3.
Link to comment
Share on other sites
8 answers to this question
Recommended Posts
Join the conversation
You can post now and register later. If you have an account, sign in now to post with your account.