jasen

@DejMar 1st question 1 5 6 3 2 7 = 1 6 5 2 3 6 = 5 1 6 7 2 3 = 5 6 1 2 7 3 = 6 1 5 7 3 2 = 6 5 1 3 7 2 1st solution 2 3 7 5 1 6 = 2 7 3 1 5 6 = 3 2 7 6 1 5 = 3 7 2 1 6 5 = 7 2 3 6 5 1 = 7 3 2 5 6 1 2nd solution 2nd question 2 9 12 4 3 18 = 2 12 9 3 4 18 = 9 2 12 18 3 4 = 9 12 2 3 18 4 = 12 2 9 18 4 3 = 12 9 2 4 18 3 = 1st solution 3 4 18 9 2 12 = 3 18 4 2 9 12 = 4 3 18 12 2 9 = 4 18 3 2 12 9 = 18 3 4 12 9 2 = 18 4 3 9 12 2 = 2nd solution Just Rotation and reflection of the circle.

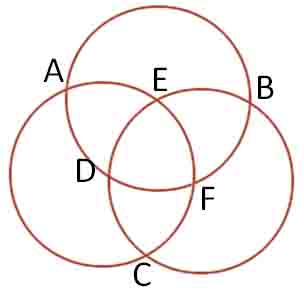
1. Easy Puzzle Put numbers 1,2,3,5,6,7 to each point, so : I. The sum of points in every circle are equal, (A+E+F+C = B+E+D+C = A+D+F+B) II. A+B+C = D+E+F There are 2 solutions. 2 .Harder Puzzle Find the value of x, then put number 2,3,4,9,12,x to each point, so : I. The product of points in every circle are equal, (A*E*F*C = B*E*D*C = A*D*F*B) II. A*B*C = D*E*F There are 2 solutions.

If you find the problem "magic cube 2x2x2" is too easy, try this. in a 2x2x2 cube Put number 1, 2,3,4,5,6,8, and 10 to every small cube, so the product of each side of the cube are equal. A*B*C*D = E*F*G*H = B*D*F*H = A*C*E*G = A*B*E*F = C*D*G*H

in a 2x2x2 cube Put number 1 to 8 to every small cube, so the sum of each side of the cube are equal. A+B+C+D = E+F+G+H = B+D+F+H = A+C+E+G = A+B+E+F = C+D+G+H

There is 1 number can't written like that. The number is 0. So the statement is wrong.

We are 3 brothers, we like multiplying our ages each other. m years later the result is m times than today n years later the result is also n times than today (m and n is not equal) we find it is interesting. How old we are?

Similar, but a bit harder puzzle : A father left 102 goats to his three sons. He promised 1/2 of the goats to the oldest son, 1/5 to the middle son, and 1/13 to the youngest son (maybe step son, just get a bit heritage ). But the sons could not divide 102 evenly. Then they call their uncle, after thinking a while the uncle come with a solution, and as thanks they give the uncle 1 goat, what is the uncle solution ?

A father left 45 goats to his three sons. He promised 1/2 of the goats to the oldest son, 1/4 to the middle son, and 1/6 to the youngest son. But the sons could not divide 45 evenly. Then they call their uncle, after thinking a while the uncle come with a solution, and as thanks they give the uncle 1 goat, what is the uncle solution ?

16,363636 minutes

If we make sequences of the numbers, we get this pattern : Month 0 1 2 3 4 5 6 7 8 9 10 11 12 sequence 1 1 3 5 11 21 43 85 171 341 683 1365 2731 This pattern is called Jacobsthal numbers, Like Fibonacci numbers, sequence follow the rule : The first two numbers in the sequence are 0 and 1, then each following number is found by adding the number before it to twice the number before that. In math expression : Jn = 2*J(n-2) + J(n-1) The formula to find the x-th number is Jn = ((2n)-(-1)n) / 3 So after 1 year there are J13 = (213 + 1) / 3 = 2731 pairs of rabbits

@logophobic : Right answer, with very clear explanation. Can you see any pattern there ? Can we generalize the problem, such as if a pair begets 3,4, or any number new pairs .... or any pairs begets any number new pairs,.... clue : generalization of fibbonacci number.

A man put a pair of rabbits in a place surrounded on all sides by a wall. How many pairs of rabbits can be produced from that pair in a year if it is supposed that every month each pair begets two new pair which from the second month on becomes productive? This problem states several important factors: • Rabbits take one month to grow up • After they have matured (for one month) it takes a pair of rabbits one more month to produce their first 2 pairs of newly born rabbits. • We assume that rabbits never die • We assume that whenever a new pair of rabbits is produced, it is always a male and a female • We assume that these rabbits live in ideal conditions • The problem begins with just one pair of newly born rabbits (a male and a female). Given all this information, how many pairs of rabbits will there be in one year (12 months)?

Right Answer, but you make a bit miscalculation. sum of 6,6,6,2 is 20, not 22.

2 mathematicians meet at their school reunion. mat 1 : Hey old friend, I heard you have 4 child, How old are they? mat 2 : Sum of their multiplicative inverse is 1, and sum of their age is your sister age. mat 1 : But, I still don't know their ages. mat 2 : 2 oldest are twin. mat 1 : ok, I know know.

2 mathematicians meet at their school reunion. mat 1 : Hey old friend, I heard you have 2 pair identical twins, How old are they? mat 2 : Sum of their multiplicative inverse is 1. mat 1 : Ok, I know.

Ok I was wrong, but I know the number is 2x3x2x5x7x2x3x11x13x19x23x5x3x29 = 68502634200

Thank you bubbled, I understand now.

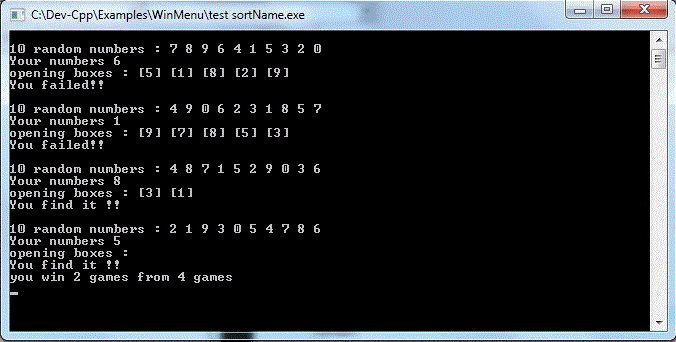
I think bubbled is right, "Sorting like" strategy, without "real sorting" will not work. I have proposed this "Sorting like" strategy, exactly like plasmid. but then I realize it was not working. I've tested it using dev-C++. the chance to find your name is only 50%, the same chance with random way opening boxes. in my program : box numbered from 0 to 9, and your number is random from 0 to 9. You can only open 5 boxes to find your name.

computer simulation proved you are right !!