bonanova

On a table is a row of fifty coins, of various denominations. Alice picks a coin from one of the ends and puts it in her pocket; then Bob chooses a coin from one of the (remaining) ends, and the alternation continues until Bob pockets the last coin. Prove that Alice can play so as to guarantee at least as much money as Bob.

Nice. Freezing would allow balancing the can sideways on a fulcrum at its beer height. Then exactly what you said is obvious. Either adding beer or subtracting beer will make the can fall toward its empty side.

I plead drowsiness. I read the puzzle incorrectly. Minus 5 obviously.

] jhawk, sorry for not replying sooner. That is the correct answer. Care to share your method? I have a clever thought process (it's not mine) that leads to it that I will share if you want to go first. It involves freezing.

Actually it's just two diagonal solutions. Apply one to x and the other to y. I just had to adjust one of them, to get a piece in each quadrant.

Nice proof. I overlooked the significance of the right angle in my solution.

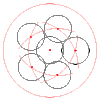
TSLF, are you sure these are the points of tangency? Edit: misunderstood. Nice!

plasmid: Bingo.

That sentence is not a true description of n because it veracity would lead to a contradiction (Similar to "This statement is false"). Therefore it is an untrue statement, and thus a false description of n. It is a self-referential paradox, but perhaps of a slightly different stripe than the liar's paradox. It describes a number truly. But in a way that is different from saying x is an integer greater than 5 and smaller than 7. It is a linguistic description, instead. But it is unambiguous. Of all numbers that can be spoken [like one hundred twenty-three (6 syllables)], there is a unique smallest number that does not require 15 or more syllables to speak it. But then using the phrase "the smallest number ... words or less" uses a different linguistic description. The usual work-around is to disallow mixing the two description types in a single discussion.

Time to plant the trees. Assuming interest on this puzzle is spent, let's close it out. Honorable mention to plasmid, whose last post was clearly on the right track.

No correct answers yet.

I would be interested to see the configuration that makes M = m * sqrt(3)

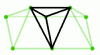
A regular tetrahedron (a solid with four faces) can be constructed from four unit-sided equilateral triangles. Four similar triangles can also be assembled to have a common vertex and a unit-square base. Adding that square creates a square pyramid (with five faces.) These two solids can now be joined into another solid: by gluing together, vertex to vertex, a triangular face from each of them. How many faces does the joined solid have?

What if there were no diagonals?

I agree with dark magician.

But if he could answer anything, he could answer yes; and you might not get home.

Number of letters in movie title, which we need to complete the answer.

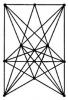
Forty toothpicks form a 4x4 checkerboard as shown in the figure. What is the smallest number of toothpicks that if removed will break the perimeter of every square: the 16 unit squares, the 9 order-2 squares, the 4 3x3 squares and of course the outside border? If you like, extend the problem to prove your answer is smallest possible. destroy every rectangle (including the squares) with fewest removals. extend the size of the square to 5x5, 6x6, 7x7 and 8x8. derive an expression for the fewest removals.

Having removed one proof, I feel obligated to supply a proof of my own that the circle can in fact be squared.

Knowing how it is second nature for my friend Y-san to solve extremal problems by equating derivatives of functions to zero, I was delighted to find a problem that can be solved with only a pencil, some drawing paper and a little thought. Here it is. Imagine an empty can that weighs 1.5 ounces. It is a perfect cylinder with weightless top and bottom, so that any asymmetry introduced by punching holes in the top can be disregarded. The can holds 12 ounces of beer; so its total weight, when filled, is 13.5 ounces. The can is 8 inches high. Without using calculus, determine the level of the beer at which the center of gravity is at its lowest point. Consider that, as beer is removed from a full can, the center of gravity is lowered. But empty and full, the center of gravity is in the same place. So there must be a filling factor where it is lowest.

Travel from one side of a curved path to the other “I had to write an IOU / To all the playas in my crew / No drinkin’ Chivas in bed / Because I’m too in the red”, e.g. Buddy to play Twister with Period of Turkish rule Shout from the ground to someone on a balcony Place to get a rotini martini Stomach problem for a stressed-out La Paz resident Apprehension of a weasel Meshed containers for edible bulbs Agent of darkness Make a sketch of part of a block and tackle Rude, unrefined member of an ugly, fanged humanoid race Someone who computes unions “Watch out for the Apple computer” Fanatical collector of old tunics bearing coats of arms Rodent willing to die for its beliefs Distilled drink from southwest Australia Where a colorful pet bird might sleep Genetic information of a person who lives in isolation Cloth used to clean a signmaker’s template Flying mammal native to far northern treeless regions British streetcar covered with a dark viscid substance Sports stadium slogan Official supervising playful conversation Small, biting fly that has landed near one’s boutonniere Weekends and holidays on a calendar Plant fluid obtained from Morocco Interconnected network of photo equipment

Quotable Bard (# letters in title) 1. O, W! HMGCATH! HBMI! OBNW, THSPI! (10) 2. F, R, C, LMYE. (12) 3. TBONTB, TITQ (6) 4. O, R, R! WATR? (14) 5. ACWH, NCSHIV. (18) 6. IMBTFOL, PO. (12)

Two to go. clue at post 4. Songs from Musicals (# letters in title of musical) D, J! (18)IGWTMROMH (12)YCBALATHYW (WYML) (7)FM (GI) (19)DYHTPS? (13)M, IABGN (9)IDKHTLH (20)TRTT (4)WSIWU? (7)GTKY (11)