Barcallica Posted August 28, 2014 Report Share Posted August 28, 2014 (edited) What is the sum of circumferences of the infinite stack of circles in the pitcure? What is the sum of areas? Edited August 28, 2014 by Barcallica Quote Link to comment Share on other sites More sharing options...
0 DeGe Posted August 28, 2014 Report Share Posted August 28, 2014 Circumference is quite straight forward Circumference of each circle is 2.pi.r So for all the circles it will be 24pi Because the length of altitude is 12 (with sides 13 & 5) Quote Link to comment Share on other sites More sharing options...
0 DeGe Posted August 28, 2014 Report Share Posted August 28, 2014 For area, had to check the web on how to calculate the radius of incircle So, the first circle has radius 10/3 So the first circle covers 2/3 of the altitude length Without going into details, I would say by symmetry that each circle covers the next 2/3rd So the second circle would be of radius = 1/3(10 - 20/3) = 10/9 ratio of each consecutive circle radius = 1/3 So sum of areas = pi(r1² + r2² + ...) = pi.(10/3)² / (1 - 1/9) = (25/4)pi Quote Link to comment Share on other sites More sharing options...
0 Barcallica Posted August 29, 2014 Author Report Share Posted August 29, 2014 For area, had to check the web on how to calculate the radius of incircle So, the first circle has radius 10/3 So the first circle covers 2/3 of the altitude length Without going into details, I would say by symmetry that each circle covers the next 2/3rd So the second circle would be of radius = 1/3(10 - 20/3) = 10/9 ratio of each consecutive circle radius = 1/3 So sum of areas = pi(r1² + r2² + ...) = pi.(10/3)² / (1 - 1/9) = (25/4)pi The first circle has radius 10/3 but doesn't cover 2/3 of the altitude length Quote Link to comment Share on other sites More sharing options...
0 bonanova Posted August 29, 2014 Report Share Posted August 29, 2014 For each circle, Ci = pi Di Sum(Ci) = pi Sum(Di) = 12 pi Quote Link to comment Share on other sites More sharing options...
0 bonanova Posted August 29, 2014 Report Share Posted August 29, 2014 Diameter D1 of the incircle is some fraction f of the triangle's height h. The next circle has a diameter D2 that is the same fraction f of the remaining height h2 = h - D1. And so forth. Here, since h = 12 and D1 = 20/3, we have f = 5/9. The successive diameters are: f h = h f = 6.666666667 f (1 - h f) = f - h f2 = 2.962962963 f (1 - f + h f2 ) = f - f2 + h f3 = 1.316872428 f (1 - f + f2 - h f3) = f - f2+ f3 - h f4 = 0.585276635 and so on. The corresponding areas are 34.90658504, 6.895127909, 1.362000575, 0.269037151 ... Taking the first 50 terms, the diameters sum to 12.00000000 And the areas sum to 43.4989752. If we note that successive diameters decrease by a factor of (1 - f) Then the areas of successive circles decrease by a factor of r = (1 - f)2. Then the areas sum to A1/(1 - r). That's just pi (10/3)2/[1 - (4/9)2] = 34.9066/.80247 = 43.4989 Quote Link to comment Share on other sites More sharing options...
Question
Barcallica
What is the sum of circumferences of the infinite stack of circles in the pitcure?
What is the sum of areas?
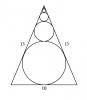
Edited by BarcallicaLink to comment
Share on other sites
5 answers to this question
Recommended Posts
Join the conversation
You can post now and register later. If you have an account, sign in now to post with your account.