A partition of a positive integer n is a way if writing n as a sum of positive integers, ignoring the order of the summands. For example, a partition of 7 is 3 + 2 + 1 + 1.
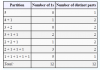
The table below shows all partitions of 5. The number of 1s column shows how many times the number 1 occurs in each partition. The number of distinct parts column shows how many distinct numbers occur in each partition. The sum for each column, over all the partitions of 5, is shown at the foot of the table.
(attached)
Let a(n) be the number of 1s in all the partitions of n. Let b(n) be the sum, over all partitions of n, of the number of distinct parts. The above table demonstrates that a(5) = b(5).
Show that, for all n, a(n) = b(n).
Question
BMAD
A partition of a positive integer n is a way if writing n as a sum of positive integers, ignoring the order of the summands. For example, a partition of 7 is 3 + 2 + 1 + 1.
The table below shows all partitions of 5. The number of 1s column shows how many times the number 1 occurs in each partition. The number of distinct parts column shows how many distinct numbers occur in each partition. The sum for each column, over all the partitions of 5, is shown at the foot of the table.
(attached)
Let a(n) be the number of 1s in all the partitions of n. Let b(n) be the sum, over all partitions of n, of the number of distinct parts. The above table demonstrates that a(5) = b(5).
Show that, for all n, a(n) = b(n).
Edited by BMADLink to comment
Share on other sites
5 answers to this question
Recommended Posts
Join the conversation
You can post now and register later. If you have an account, sign in now to post with your account.