What do you mean he dont have 23 as one of the co-ordinates? It is present in 4th row. Do you mean u need it at the starting position?

What I mean by "coordinates" are the numbers either written down the side of the grid or across the top of it.

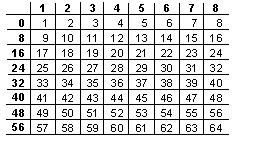
I believe in the original problem statement you mean that "23" is one of the axis coordinates?

Yes.

Sorry! You don't have 23 as one of the coordinates.

One set of eight positive integers is written down the

side of an 8x8 square grid, another set of eight across

the top. The entry in any cell of the grid is the sum

of the corresponding side and top coordinates. These

entries are the numbers from 1 to 64 inclusive. If

one of the coordinates is 23, what are the others?

ok guess number two.. i mean definitely the answer number 2

so i relooked at it and the mistake i missed was 1wb at the beggining

so

summation E prob white W prob black B

E=WE+W^2E+W

E=W/(1-W-W^2)=8131.....

but that is forgetting the B

so E=8131.578947*B=3106.263158

Im pretty sure this is right now

anyway I tried to look up this problem you were talking about. can you tell me what this problem is or what website i could find it on.

Spot on! Part 1 is indeed that!

I can't give you a website because I got it from some privately published

papers containing original Walter Penney problems. I'm glad you liked this

one -- I'll put out more from time to time. I won't do it too quickly, though.

Walter Penney was a master puzzle maker and I don't want to monopolize

things. Walter died in 2000 at the age of 87.

I don't agree with your part 1 and I can't seem to reproduce how you got it. But, I'm sure it's a small matter. Congrats on getting part 2 spot on. I just think it's pretty cool that a single ball makes all that difference!

You'r part 1 answer was for the problem if the Fibonacci started 1,1,2,3,5,.... instead of 0,1,1,2,3,5..... You had a neat, simple way of doing it, too.

Here is my modification of a puzzle by the late

great puzzle maker, Walter Penney:

There are 309 white balls and 191 black balls in

a bag. A man makes a deal in which he draws balls

one at a time from the bag, replacing and mixing

after each draw, and if the first black ball is

drawn on the Nth trial, he is to receive a number

of dollars equal to the Nth Fibonacci number

(0,1,1,2,3,5,8,13,... for N=1,2,3,4,5,6,7,8,...).

Two questions:

1. What is the expected payoff for the man?

2. If he were to surreptitiously place one more

white ball in the bag, by how much does it improve

his expectation from that in question 1?

Suppose we have a group of N men and another group

of N women. Each man makes a preferential list of

women he could marry (ties are not allowed). Similarly,

each woman makes a preferential list of men she could

marry. It is always possible to pair up all of these

people into N man-woman pairs so that the pairing is

stable. By stable I mean that, if we take any two

pairs in this pairing, (m1,w1) and (m2,w2) say,

then it is never the case that [m1 would prefer w2

over w1] AND [w2 would prefer m1 over m2]. That is,

it is never the case that m1 and w2 would both prefer

each other to their paired partners. An easy proof

of this can be found at:

http://tinyurl.com/nze7cr

If, however, we have to pair up 2N people to be

roommates, that's a different matter! If each of

these people make a preferential list of possible

roommates (of all 2N-1 other people -- with no ties),

then it is not always possible to make a stable pairing

according to the definition above. What is the smallest

N(>2) such that a stable pairing is not always possible?

For your value of N, give a preferential order (1

being most preferable to 2N-1 being least preferable)

for each of the 2N people, for which a stable pairing

cannot be made.

A=4 Yields G=16 and F=64, I think there are no more other than in my first post above.

If you define A=F/G, then A is a (possibly not an integer) number > 1. Then, Replace F in the OP equation by AG. Solving for G, we get G=A^((A+2)/(A+1)) which makes F=A^((2A+1)/(A-1)). I think the only solutions in the integers for F and G is when A=2.

Determine all possible pair(s) (F, G) of positive integers, with F > G, such that: F^F+2G = G^G+2F

that F=32 and G=16 is the only answer. Still working on it....

in the classic tower of hanoi puzzle, you are given 5-7 disks on top of each-other, with each disk increasing in size from top to bottom. there is a rod standing vertically going through the center of the disks, and two more vertical rods that are empty. your goal is to move one disk at a time such that no bigger disk is placed on a smaller disk, and all 5-7 disks end up stacked again on a new rod.

well now for the twist. there are now 3 empty vertical rods and a new restriction. that restriction is that you can only place a smaller disk on top a particular larger disk, or a larger disk onto a smaller one, once. for example, if you put the first disk directly on top of the fourth disk, you cannot do so again.

try to solve it with 5 disks, then 6 disks, then 7 disks.

can this new puzzle be solved? if so, what's the solution?

Quite easy. It only requires 1 empty rod. Just move each disk, in order, from the first rod to the second one. Then go back. Each disk was placed on top of a particular other one just once.

Quite easy. It only requires 1 empty rod. Just move each disk, in order, from the first rod to the second one. Then go back taking each disk from the second rod to the first. Each disk was placed on top of a particular other one just once. Or perhaps I am missing something?

What's wrong with the spoiler? I get my last 2 posts after each other. The second spoiler is what I mean to say.

Consider a horse race at a racetrack. Further consider what

happens when people bet that a horse will win that race.

A percentage, X (<100%), of the total money bet on these horses

to win is returned to the people who have bet on the winning

horse. A person's share of the winnings is proportional to

how much he bet. The rest, (1-X) of the money bet, is used

to pay for expenses and prizes to the horse owners. This

is, basically, the definition of parimutuel betting.

Now, the racetrack continuously updates odds for each horse

on a large display for all to see. These updates stop at the

start of the race when no further betting is allowed. These

odds tell the bettors what the return on their bet would be

should their horse win that race. The odds are posted as a

fraction A/B which means that for each dollar the bettor bet,

he will receive $((A/B)+1) should his horse win. So, for

example, if the bettor bet $1 and the odds posted as 15/1 just

as the race began, the track would pay the bettor $16 ($15

plus a return of his $1 bet). Odds of 8/5 would return $2.60

($1.60 plus his $1 bet).

Suppose the odds posted at the start of a 7 horse race were

15/1, 7/2, 8/5, 12/1, 5/2, 6/1, and 10/1. You can derive a

reasonable estimate for X (defined in the first paragraph)

from this information. What value would you give X and why?

I'm not positive this is completely correct. I analyzed the score for a single frame by itself and multiplied by 10. There may be correlation between frames that throw things off, but here's my work/guess...

The average score after one throw of the ball if there are 10 pins is 5. So if you get a spare, you can essentially just add 5.

Ignoring the possibility of a strike for the moment, we can use the above to find the average for a frame.

if you get a gutter ball on the first throw, your average score for the frame will be 60/11 (0+1+2+3+4+5+6+7+8+9+15 <-because of +5 for spare)

similarly for 1-9 pins

0:60/11

1:60/10

2:59/9

3:57/8

4:54/7

5:50/6

6:45/5

7:39/4

8:32/3

9:24/2

The sum of the above is 457931/5544.

The average score for a frame will be (average score for strike + (457931/5544))/11.

Now we can analyze what happens if you get a strike. If you get a strike you get an automatic 10 points and the score for the two next rolls. If you get another strike then you get 10 points plus another roll (= average of 5 more points). So if you get another strike the total will be the initial 10 plus an average of 15.

We can do a similar thing to above for combinations for the rest, only it is simpler this time due to the lack of spares.

0:55/11

1:55/10

2:54/9

3:52/8

4:49/7

5:45/6

6:40/5

7:34/4

8:27/3

9:19/2

The sum of the above is 145/2.

The average score for a frame that you initially get a strike is then 10 + (15 + (145/2) )/11

= 10 + (175/2)/11 = 10 + 175/22 = (220+175)/22 = 395/22. Plugging this into the earlier equation gives:

((395/22) + (457931/5544))/11 = (99540 + 457931)/60984 = 557471/60984. So about an average of 9.141267 per frame. For a whole game, this would average 91.41267.

Did I get it? Or is there a mistake here somewhere?

EventHorizon has it! Just to check things, I wrote a program to simulate random games. After 1,000,000,000 random games, the average score from the simulator was 91.4135. Congrats!

If the first ball is a gutter, the average for the 2nd roll will be 5. If the first is 1 pin, the average 2nd will be 4.5, etc. The total pins for each of these alternatives will be 5, 5,5, 6, etc. for an expected pin count of 7.5. There is a 1/11th chance that you will roll a strike. The chances of a spare depend on the first roll but will be 1/11 if the first is a gutter, 1/10 if the first ball gets 1 pin, etc. If we give 10 points fro a Spare and 20 points for a strike, The expected total point for each 11 possibilies are as follows

First Roll-----Expected Score

0--------------5.909

1--------------6.5

2--------------7.1

3--------------7.75

4--------------8.4

5--------------9.17

6--------------10

7--------------11

8--------------12.33

9--------------14.5

10-------------30

This is an average of 11.15 per frame or 115 per game.

This is an over estimation as it gives full points benefit for each spare or strike. If someone wants to make that correction, I'll be interested in seeing the approach

I didn't check your average of 11.15 per frame, but if it is that, then you get 111.5 per game. A very nice upper bound!

I used to like to go ten pin bowling quite a bit.

I remember that I scored 83 in my first ever game.

It occurred to me that I should compare how I did

in that game to the expected score in a type of

random bowling.

In random bowling, if there are N>0 pins standing,

there is an equal probability for each of the

possible outcomes of your bowl: knocking down

0 pins, 1 pin, ..., N pins. Each of these outcomes

has probability 1/(N+1). The game is scored the

way standard 10-pin bowling is scored.

So, for example, at the beginning of a frame, your

first bowl has 1/11 probability of getting a strike,

a 1/11 probability of knocking nine pins down, and

so on down to a 1/11 probability of knocking no

pins down. If you didn't bowl a strike, there are

some number of pins, say X, still standing. On

your next throw to complete the frame, you have a

1/(X+1) chance of knocking all X down for a spare,

a 1/(X+1) chance of knocking down X-1 pins, and

so on down to a 1/(X+1) chance of knocking none of

them down.

With this scenario, what is your expected score?

Looks correct but how did you go about solving it?

Here's how I solved it: Notice that if you get the 5th row, you can construct the rest of it upwards from 4th row to the 1st. Notice also that 15 MUST be in the bottom row and probably 14 and 13 are there as well. I assumed, then, that 13 and 14 are on the bottom. Now, there are 66 choices for the other two 5th row numbers. I started with 6 for one of the numbers (in the middle of the possible 1 thru 12) -- it turned out to be a very lucky start. The other number I guessed starting at 12 and working my way down. Now there are 60 permutations of the bottom row to look at (we don't try the reverse of something we already tried). I laboriousely went through them and tried to reconstruct the rack from each one. Nearly all of them gave me two of the same number very quickly. And sometimes a particular string can't happen (like 13,14,15 which would make two 1s in the fourth row immediately). Checking cases is actually quite fast once you get the hang of it. It took a little more than an hour to find the correct answer. If I hadn't made the lucky start of 6 in the bottom, I probably would have quit by now.

first row: 5 ; second row: 4,9 ; third row: 7,11,2 ; fourth row: 8,1,12,10 ; fifth row: 6,14,15,3,13

Such as now...

and buy only 4 tickets, costing $68.01 per mathematician

Would you post precisely which tickets they would be? Just assume that the mathematicians want to cover all subsets of 6 from the numbers {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16}. I can't seem to find a set of tickets as you describe.

(Webmaster, There seems to be a spoiler problem)

This seems too easy again! May be I am still missing something!!

A minimum of 16 tickets would be needed (¹⁶C₁₅)

Buy 16 tickets of 15-Play leaving out 16the number in first, 15th number in second, 14th in the third... and so on

The cost would be 16 * 5005 = 80080 and cost per mathematician = 80080/143 = $560

No, you're not missing something. You have a convincing argument that you have found an upper bound. Can you prove that it can't be done with fewer tickets?

You have 4 biased coins. They look identical. They have the following respective probability to land up head: 1/5, 2/5, 3/5, 4/5. You accidentally jumbled the four coins together and now you don't know which is which.

Lets say that you have to determine the coin's identities by flipping them and observe the outcomes. Assume you can flip as many times as you like, and you can choose any coin at any flip.

1) what's lowest expect number of flip required to identify 1 coin with 95% certainty? that is, you want the lowest expected number of flips to correctly identify 1 coin 95% of the time.

Hard bonus.

2) What is the lowest expected number of flips required to correctly identify all 4 with 95% certainty?

35 (35 if you're flipping the 1/5 or 4/5 coins; 45 if you're flipping the 2/5 or 3/5 coins)

I would like to restate the problem:

The country of Ozendia has a weekly lottery drawing.

A set of 6 numbers are drawn without replacement from

the set of numbers {1,2,3,...,40} randomly. A play

of this lottery consists of buying a ticket with a

buyer-chosen guess as to what these 6 numbers will be.

The drawing order of the numbers does not matter.

Each play costs $1. The payoff is usually in the

multi-million dollar range and it is a percentage of

the ticket sales since the last winner. Ozendians

love to gamble, so there is usually a small number

of winning tickets each week. If this number is

greater than one, the jackpot is shared equally among

the winning tickets. So far, this is much like many

lotteries familiar to most people.

Ozendians are social gamblers. That is, very often

a group of people will buy a bunch of tickets with

any winnigs divided up equitably to the group

members. Ozendian lottery officials want to encourage

this behavior as they believe it increases ticket

sales. So they developed a scheme to allow groups

to buy lots of sets of numbers on a single ticket.

They have what they call a 7-play ticket. You get

to choose 7 numbers on a 7-play and the ticket wins

if any subset of 6 of these 7 numbers is picked.

Since this is equivalent to buying 7 different

normal tickets, the cost is $7 for this kind of ticket.

Similarly, they have an 8-play, which is equivalent

to 28 standard tickets and so, costs $28. In fact,

they have N-play tickets right up to N=15 which

costs a whopping $5005! They, in fact have all

N-plays for N=6,7,8,9,10,11,12,13,14,15 (I included

the standard game as a 6-play).

Well (wouldn't you know it?), there's a group of 143

mathematicians in the Ozendian Defence Department who

wish to buy the equivalent of a 16-play costing $8008

($56 for each mathematician). They have decided on

their 16 favorite numbers. They wish to cover all

subsets of 6 out of their 16 numbers using standard

N-play tickets (N=6 to 15) with as few N-play tickets

as possible (including the standard game as 6-play).

After all, they are mathematicians, so they can afford

to pay a bit more than $56 each!

What is the minimum number of N-play tickets

which would achieve the cover of all subsets of 6

out of the 16 numbers? What would they cost?

They could buy 8008 (16C6) standard tickets (6-play) for $1 each. So, the minimum amount cannot be more than $56 each for the 143 mathematicians. And you wrote that they could afford to pay a bit more than $56. Am I missing something or is that statement in the question redundant??

Sorry, I meant to ask:

What is the minimum number of N-play tickets

which would achieve the cover of all subsets of 6

out of the 16 numbers?

The country of Ozendia has a weekly lottery drawing.

A set of 6 numbers are drawn without replacement from

the set of numbers {1,2,3,...,40} randomly. A play

of this lottery consists of buying a ticket with a

buyer-chosen guess as to what these 6 numbers will be.

The drawing order of the numbers does not matter.

Each play costs $1. The payoff is usually in the

multi-million dollar range and it is a percentage of

the ticket sales since the last winner. Ozendians

love to gamble, so there is usually a small number

of winning tickets each week. If this number is

greater than one, the jackpot is shared equally among

the winning tickets. So far, this is much like many

lotteries familiar to most people.

Ozendians are social gamblers. That is, very often

a group of people will buy a bunch of tickets with

any winnigs divided up equitably to the group

members. Ozendian lottery officials want to encourage

this behavior as they believe it increases ticket

sales. So they developed a scheme to allow groups

to buy lots of sets of numbers on a single ticket.

They have what they call a 7-play ticket. You get

to choose 7 numbers on a 7-play and the ticket wins

if any subset of 6 of these 7 numbers is picked.

Since this is equivalent to buying 7 different

normal tickets, the cost is $7 for this kind of ticket.

Similarly, they have an 8-play, which is equivalent

to 28 standard tickets and so, costs $28. In fact,

they have N-play tickets right up to N=15 which

costs a whopping $5005! They, in fact have all

N-plays for N=6,7,8,9,10,11,12,13,14,15 (I included

the standard game as a 6-play).

Well (wouldn't you know it?), there's a group of 143

mathematicians in the Ozendian Defence Department who

wish to buy the equivalent of a 16-play costing $8008

($56 for each mathematician). They have decided on

their 16 favorite numbers. They wish to cover all

subsets of 6 out of their 16 numbers using standard

N-play tickets (N=6 to 15) at minimal cost. After all,

they are mathematicians, so they can afford to pay a

bit more than $56 each!

How many of each type of N-play tickets (include the

standatd game as 6-play) are necessary to achieve

minimal cost? What is the cost per play?

Shouldn't it be a bit less? You're probably thinking that 1/8 = .12000

1/8 = .125. If you have 100 or 102 blades, you'll have a probability of 0.1256451 or 0.1244011, respectively. Still seems an awful lot to me, but induction said so, so it must be so.

Oops, you'r right! Stupid slip up on my part. Thanks!