Prime

We are moving toward the solution, but no solution yet. I am going to make couple hints here, which should help solving this problem properly. The two problems shown in this post are the easier problems on that test. I don’t think they consider those as calculus problems. Those two are arithmetic and algebra problems. Problem 3 on that test is a calculus problem. It involves a basic derivative and integral of a polynomial. But the setup leads to a rather complex and lengthy solution. Problem 4 is a trigonometry problem involving knowledge of some basic formulas, like cosine of doubled angle and other behavior of trigonometric functions. But the setup, again, leads to a very lengthy and complex solution requiring testing of many different cases. So I don’t think it is worth showing those here. (Too much work solving them). However, problem 5, a geometry problem, I could show when and if the logarithm is solved.

1. Are players set in a straight line, circle, or how? 2. Are we to assume that a player does not get a second shot until everyone else alive made their shot? (Your setup allows giving first shot to someone away from you, then taking all the consequtive shots for yourself.) 3. If players were "intelligent" and their objective was to survive, they would avoid participating in a game like that. 4. Some people may find offensive your use of real persons' names as participants in such duel.

It is in the general neighborhood of the solution. However, they don't give multiple choice test in that university. You must show how you arrive to the answer. To solve, you need to simplify the expression somewhat. Also, you must mind the values of x, where log is undefined.

Here is the Problem 1 from that test. This one is not all that difficult, also. 1. Solve the inequality: log(2x+7)(x2+4x+4) < 2log(x2)|x|

Within the Brainden framework, your solution (by trial and error) is absolutely correct. And trial and error within some defined boundary conditions is a valid analytical method. On that test, I am sure, they wouldn’t give you a full credit, as they looked for an algebraic solution there. Your method does not prove that 23 is the only solution, but that’s not a flaw, since my statement of the problem (my translation rather) in no way implied that requirement. I mentioned zero, because I didn’t see in your trial and error solution test cases for it. Like number 30, for example, which falls within the parameters that you specified. I posted that problem as a curiosity item. To show what kind of admission tests they give in that University in Russia. Keep in mind, there is a time limit on the admission test. Even so, that problem was meant as a gift. Others looked much worse.

Better yet. Drop couple bags from the 10th floor down on the street. Go out, and pick them up. If security stops you -- you were conducting tests to find fake coins. Just carrying out your assignment, you are in no way culpable of any wrongdoing. And if they ask why you headed for the train station with those bags -- that's because you thought to find functioning scales there.

Perhaps gold is heavier than lead. But, comon, we have to respect what Galileo had found and described some 400 years ago. In absense friction, objects fall at the same rate regardless of their weight.

That's the solution. Also, partial credit to Armcie for same correct equation. Let me show a bit more detailed work. That is part analytical, part trial and error. Also, the even digit could be zero.

You have the correct answer. But this wouldn't pass. (Or you'd get a small partial credit.) They want to see your work. This problem must be solved analytically, not just by trial and error.

I think...

Lead is heavier than gold. And it is common enough. Also, your gravity test would not work. Especially so with the assumption that friction is the same. In that case coins of different weights will roll down at the same rate, same as free fall.

While surfing the Net, I came upon a sample admission test in math for the MEPhI (Moscow Engineering Physics Institute). As I was looking at those 5 problems, a profound sense of futility slowly rose from the pit of my stomach. But upon a closer examination I realized that the problem #2 I could solve and quickly enough. Here is my English translation thereof. Enjoy. 2. If you multiply the first digit of a certain two-digit number by 4, the second digit by 6 and add the results, then the resulting sum is going to be 13 greater than the sum of the squares of those two digits. Find such two-digit number. That is the easiest (or second easiest) of the 5 problems. The other four I do not want to show here, as I find them unsuitable.

Two objects of the same shape will take exact same amount of time to fall down the elevator shaft regardless of their weight.

Umm...I don't get question 4 about the trams...care to elaborate? Also correct answers. Except, I didn't get, what did 1.4 mean for the problem 5?

After solving your system of equations, I arrived to the same answer as in the book. So you must have made an error in calculations somewhere. You'd get a partial credit for constructing a correct system of equations. Whether it would be enough to pass, depended on competition. (And if you didn't pass -- 2 years of military service it was.) I was more lucky in constructing my equations. They yielded smaller intermediate results. Problems 3 and 4 are now officially sooved.

Sorry, that's not the answer I got. (And mine matched the one in the book.) Interesting way of constructing equations though. Perhaps, still some algebra mistakes in resolving the system. To be fair, the time limit for a problem like that is not like time limit on ACT, where you get 60 min to solve 60 problems. A typical Russian university admission math test would be something like 4 or 5 problems with 4 hours to solve them. So if you can solve this under one hour you'd be OK, as long as you also could simplify multistory, three line long trigonometrical and algebraic equations in the other part of the test fast enough. Depending on university, those tests were designed to sieve the competition of 3 - 15 applicants per one available place.

When I went to school, we used printed tables. Although we did study slide rule at some point, high school students in Russia could not be expected to be able to find/afford their own slide rule. The actual answer given in the book for this problem is ~4.7 years. Perhaps, there were some set requirements for rounding answers at those tests. Sorry, that's incorrect. You overlooked that ...

Interesting! I guess, that depends on your location. In the US high school students do rely on calculators. Too much so, in my opinion. The problems 3, 4, and 5 are still unsolved.

That's the correct answer. Interesting to note, school students didn't have calculators back in 1875. Correct solution. Dirigible is a blimp.

I presume, the question is: "How long does it take each snail to cross the path?"

Sorry, the question #1 meant 0.1 annual rate of increase. Which is 10%. While your solution method is correct, the answer is different. That is to say you'd get a partial credit for this one on the exam, something like 80%.

Here are few elementary algebra problems from a collection of Russian math test problems for school students. While they may appear rudimentary to math students, keep in mind that those present just an example of algebra test problems that every high school graduate was expected to solve within a short time limit. Compare that to some standard tests of today, like ACT and SAT in the United States. Also, the arrangement of the problems gives an interesting historical perspective. Enjoy. 1. Several years ago there were 10,000 trees in the forest. Now there are 15,600 trees in the forest. Over how many years the growth took place, if each year the number of trees increases by 0.1? (From a High School Diploma test, 1875). 2. A dirigible first traveled 40 km going against a 30 km/hr wind and then returned, spending 2.5 hours total for the round trip. Find the dirigible’s speed in a still air. (From a High School Diploma test, 1913) 3. A collective farm worker, set out from his village to the railroad station. Having walked 3 km after one hour, he observed that if he continued at the same speed, he would arrive 40 min late for his train. So he paced up and walked at 4 km/hr for the rest of the trip. Thus he arrived to the station 45 min before his train’s scheduled departure. Find the distance from the village to the station. (From Math Olympiads, ~6th grade level, 1950s) 4. A man walked every day along 1 km stretch of the streetcar rail. After 1 month he had counted 45 passing trams that moved in the same direction and 120 trams that moved toward him. Given that the man walked 1 km in 12 min, find the speed of tram. (From Military School tests, 1947). 5. Two bodies simultaneously departed from point A on the circumference of a circle, moving along the circumference in the opposite directions. When the two bodies met, it turned out the first body had traveled the distance 7 cm greater than the second. After the meeting the bodies continued their motion and the first body arrived to the point A 4 seconds later, whereas the second body arrived to the point A 9 seconds later. Find the circumference. (From a university admission test, 1958) *Note: Each university in Russia had their own admission test.

Why does the Russian puzzle book feature Manhattan and Queens instead of the Red Square and Profsouznaya street? Or, at least, the Brighton Beach? By the way, I saw this one problem in a Russian puzzle book for the 3rd -5th grades some 40 years ago, but it used steam boats leaving the harbors A and B.

I thought the whole idea was that you have only 3 cubes with the letters, which leave you no spare sides. Therefore, only one side with n/u. How can you use it twice? Place couple of mirrors next to it, perhaps?

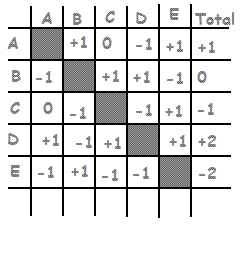
I've sent you my Fish3 the Flipper again. Here is an example of what a round-robin tournament table may look like. Perhaps, you could make one like that filling the participant names and publish the latest standings once a day, just to keep the suspense.