rocdocmac
-
Posts
433 -
Joined
-
Last visited
-
Days Won
15
Content Type
Profiles
Forums
Events
Gallery
Blogs
Posts posted by rocdocmac
-
-
Thank you Bonanova for your input!
To all participants ...
The 3-cubelet removal question has now been submitted as a separate new entry called "Cubicle Stack #2" since the thread sort of "got lost" in the original Cubicle Stack discussion after having been solved!
SpoilerIndeed, the images of the 22 solutions posted for the 2-cubelet removal ought to be very handy! But there are a whole lot of more combinations now. Happy playing around, if you have the time of course!
-
∫1/(2x) = ½ln|x| + c.
ln|2x| = ln|x| + ln(2), where ln(2) is a constant
-
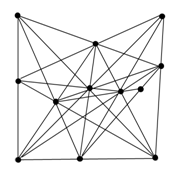
Suppose 27 identical cubes are glued together to form a cubical stack, as illustrated below.
If one of the small cubes is omitted, four distinct shapes are possible. If two of the small cubes are omitted rather than just one, twenty-two distinct shapes are possible (see previously submitted Cubicle Stack at BrainDen.com).
Now, if three of the cubelets are omitted, how many distinct shapes are possible?
-
Spoiler
Not the most elegant sketch, but here's one way to plant 12 trees in 18 rows of 3 each.
Thus, if Al and Chuck told the truth and Bert tried (but failed) to make a sketch for the inspector (none of the trisectors colinear), then Dick is the third truth teller. So far all four (living) brothers already got the blame, but it now appears that Bert is in trouble! Bert also mentioned that he "was analyzing random polygons with 3 sides" ... why didn't he say triangles?
-
Spoiler
I misinterpreted Bert's statement! Doesn't work on paper the way I put it!
-
My final answer:
SpoilerDick is most probably the lier. Maybe that's why he ran into the woods?
One can almost certainly plant 12 trees in such a way that you have 18 rows with three trees per row ... meaning that Chuck's statement is true.
-
Spoiler
It is possible to plant 12 trees in a maximum of 19 rows with each row containing 3 trees in a straight line. Thus, 18 rows with three trees in line seems feasible, but what would the configuration look like? Still a humdinger! C'mon Chuck, show us to prove you are guiltless or not!
-
Spoiler
The statements of the first two brothers appear to hold.
1. For any integer, if x+y+z=0, then x*y*z = (x³+y³+z³)/3
2. α + β + γ = 180; (α/3+β/3+γ/3) = (α + β + γ)/3 = 180/3 = 60
Chuck's statement will hold if it can be shown that it's possible to plant 12 trees in such a way that you get 18 straight rows with 3 trees each, the culprit would be Dick. If not proven, then Chuck is the liar and Dick is safe.
I think Chuck is the liar
-
Does anyone want to attempt figuring out the number of patterns if three of the cubelets are omitted rather than one or two?
-
Spoiler
Oops!
Maximum V/A ratio = 0.5 (D2). It's zero for D1, not infinity!
Spoiler
-
Spoiler
i.e. ... ∑ (0 + 2 + π + 4π/3 + π² + 8π²/15 + ...)
-
What is the sum of the unit volumes of n-dimensional spheres for the infinite series 1, 2r, πr² , ⁴/₃ πr3, ...
-
Spoiler
Well done!
Thalia eventually got the 22 right (albeit with a question mark). Slashpuzzler followed with the correct answer afterwards.
Attaching some images to show the 4 E+C combinations, a second as a summary and a third to show how each fused cube looks like when two cubicles are removed.
-
Spoiler
Close, but no cigar!
Three or more participants have the combinations with respect to some of the possibilities (K+F/C/E, F+F, F+C, F+E, C+C and E+E correct. No-one so far is spot-on with the number of edge versus corner (C+E) combinations, however!
[K = kernel, core or center; F = face or middle, C = corner, E = edge]
-
Spoiler
No correct answer yet, so revise your own individual counts of possible combinations. Someone ought to get it right soon!
Remember that shapes obtained by rotation do not count, whereas mirror images are fine.
-
Spoiler
BMAD wears a blue hat and the other two wear yellow hats
-
Spoiler
Who else wants to give it a stab?
-
Spoiler
One can go higher!
-
My question and image seem to have disappeared!
Suppose 27 identical cubes are glued together to form a cubical stack, as illustrated below. If one of the small cubes is omitted, four distinct shapes are possible: one in which the omitted cube is at a corner of the stack, one in which it is in the middle of an edge of the stack, one in which it is in the middle of a side of the stack, and one in which it is at the core of the stack. If two of the small cubes are omitted rather than just one, how many distinct shapes are possible?
-
Spoiler
You cannot use the sum rule of differentiation to determine the derivative of x + x + x + x + x … (repeated x times) since the x in “x times” is not a number, but a variable. The sum rule in differentiation is
(f1(x) + f2(x) + ... + fk(x))' = f '1(x) + f '2(x) + ... + f 'k(x), where k is any positive integer.
-
Spoiler
row 1: 6 (left) & 54 (right) ... 6 + 5 + 4 =15 (middle)
row 3: 12 (left) & 32 (right) ... 1 + 2 + 3 + 2 = 8 (middle)
Therefore, row 2: 10 (left) & 20 (right) ... 1 + 0 + 2 + 0 = 3 (middle)
-
Spoiler
(1) 5 - 4 + 5 = 6
(2) 3 = 4 + 5 - 6
(3) 3 - 4 + 6 = 5
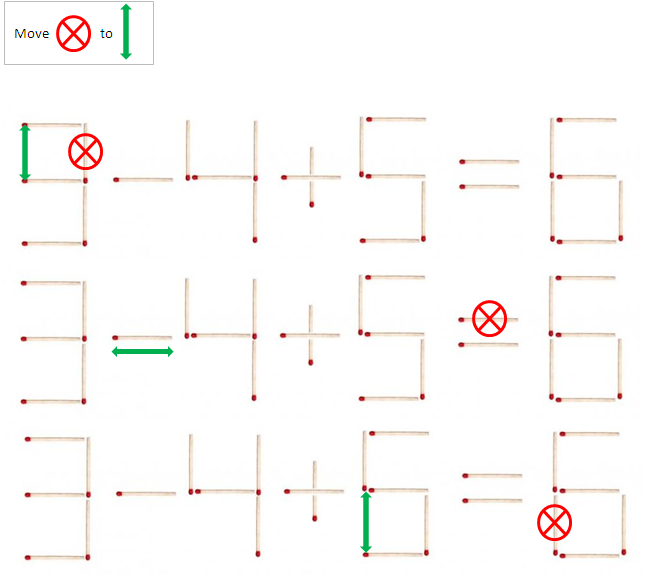SpoilerAlso
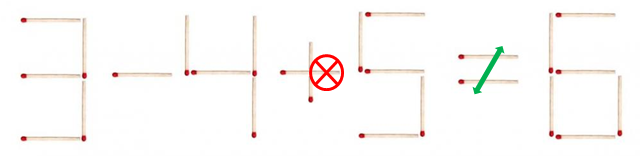
SpoilerSorry, I meant ...
-
-
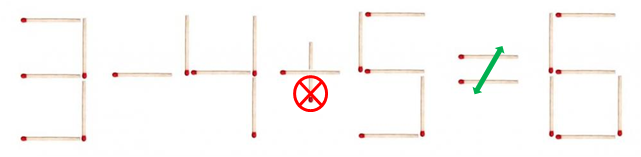
Reason for giving 12:
Spoiler(15-6)*6=54
(12-10)*10=20
(12-8)*8=32
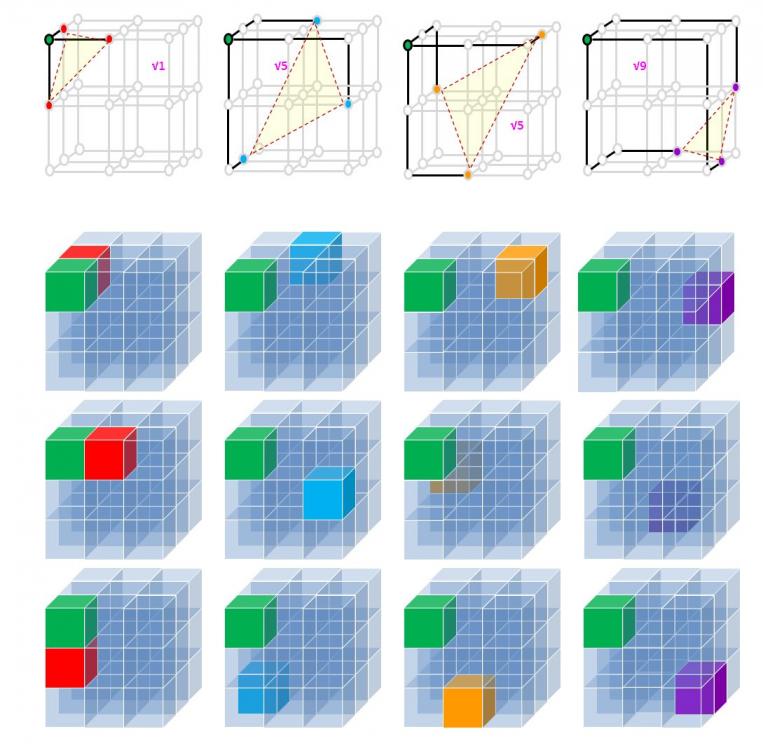
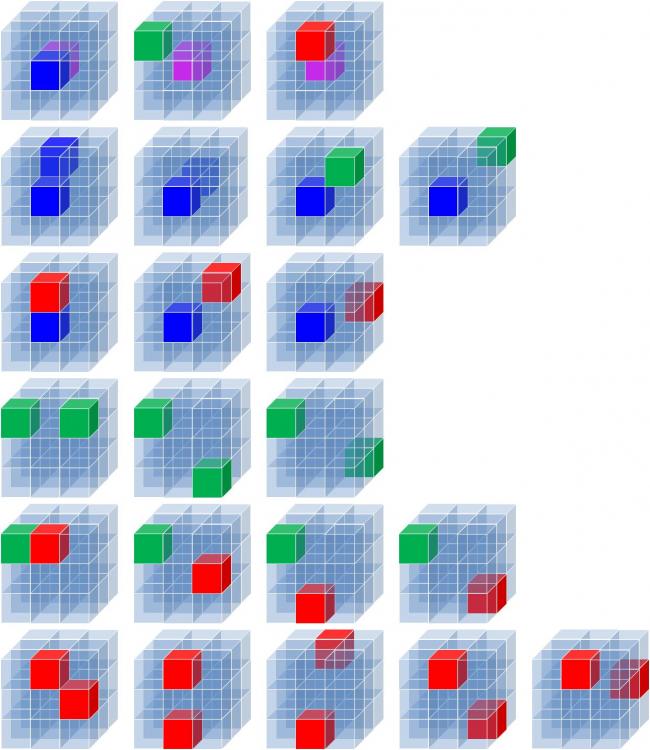
Whodunit?
in New Logic/Math Puzzles
Posted
Back to square 1!