
DeGe
-
Posts
133 -
Joined
-
Last visited
-
Days Won
8
Content Type
Profiles
Forums
Events
Gallery
Blogs
Posts posted by DeGe
-
-
72; Add one to the next prime number
-
Granted... you now exist only in the cartoon world getting beaten by a mouse all day long
Ironic, I came on this forum for the first time due to a msg from Kestrelknight on another forum and had to post this...

-
In any case, C can always demand a password protected document with the actual translation of X,Y and Z before making the choice. Once C makes the choice, then A or B can reveal the password so that C can open the document and confirm the choice made. Of course, this still leaves the option of C breaking the password if he's a master hacker or something. But I think that would be a stretch and can still be avoided by using a very strong password (encrypting) and asking C to make his choice within a minute of getting the details (so that he won't have time trying to unlock the code). They can all be online to make sure C responds immediately.
This is the key point. It prevents any cheating and is fair to all 3.
-
Aha, ok then here's another idea:
First everyone sends everyone their preference, and they all email each other to make sure they have the same information.
Now each one of the three generates a random 1024 bit number, call it x1 x2 x3, but first before revealing those numbers they share a cryprographically secure hash of these numbers (say SHA-512), and then after they make sure everyone know all 3 hashes they share the actual x1 x2 x3, they calculate x1+x2+x3 (mod 2^1024) and treat that as a uniform sampled random number, you can then use it to pick a restaurant
Although technically speaking, I don't think there is any flaw in this solution, using this method is way too complicated.
-
Persons A and B agree upon (via email) a code to mask the restaurant actual names. For example, X=1, Y=2 and Z=3. This information will not be provided to C.
C will then be asked to pick between X , Y and Z. Once C picks up the value, A and B then reveal what it corresponds to and they all have to go to that restaurant.
What if C thinks that A and B will rig the outcome by changing the restaurant codes once they know the value from C? A possibility if both A and B do not like the restaurant chosen by C?
-
The fourth person could be influenced by any of the three!
How can a random person, whom none of them has ever met, be influenced on such a mundane choice? And don't say money, because it would make no sense to pay someone for such a simple thing.
How will you decide who will choose the "random person" then when the only contact they have is through emails?
they can agree to random chance it.
roll a dice. 1 or 4 equals restaurant 1, 2 or 5; 2; 3 or 6, 3
Who will roll the dice then?
-
they agreed to have one of them ask a fourth, random person to choose for them, then tell the others the choice made?
The fourth person could be influenced by any of the three!
phaze has a valid point regarding answers from Anza and dgreening.
-
3 friends (A, B, C) want to decide on which restaurant to go to on the weekend. They all have a different preference (Restaurant 1,2, 3).
The only communication between them before the weekend (meeting at the restaurant decided) is through e-mails.
How can they together decide which restaurant to go to in a fair process which involves all 3 of them in the decision making?
-
Prime numbers (greater than 3) are of the form 6n+1 or 6n-1
Since approximating 6n+1 using a rational number will be difficult as n increases, lets consider only 6n-1 cases.
As we are rounding down the numbers, an expression close to but only just less than 6 that gives all the numbers of form 6n-1, will have almost a third of the numbers prime.
Therefore using 5.99999999... we would get all 6n-1 numbers and nearly 1/3 of these numbers would be prime
-
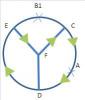
To reach point A after leaving the castle at B, he first has to pass through the intersection at C, making D his
second intersection. He will continue to turn right onto DF, turn left at F, turn right at E, and return home. In fact, you just demonstrated one case where the prince ends up returning back at his starting point, which supports the prince's assertion.I assumed that the prince uses this technique to get home from anywhere on the island and not necessarily for getting to that place.
-
I think this logic is not correct.
Consider a simple road network as below.The prince is at point A, and wants to reach his home at B
Using his logic, he stays on DE (his first intersection), turns right to EF (2nd intersection), then turns left at 3rd intersection to FC,and right again on 4th intersection towards CD.
He will then keep moving on these roads only without ever going to the roads EC and DF.
-
This is a good question. With every step that I take, it gets more and more complex

I am probably not using the right technique!
-
Your explanation is not the one I was looking for - although I have to admit that since this is an original problem, I am not quite sure of my own solution. Could you explain how you came upon this conclusion: "Then for any point within this area, there is a line that passes through this point at each and every angle from 0 to 360 degrees"? Isn't it sufficient for every point within the area to have just one line that passes through it?
Within an "area", if you consider any random point, then all the points around it must also be colored, meaning that there must be lines through this point in all possible directions, hence the 0 to 360 degree comment. The problem is similar to the triangle problem where the naked eye tells you that there is a "black area" but infact it is so because you choose the thickness of a point, or a line in this case. If instead of point bouncing off, you had a ball bouncing, I would definitely agree with Bonanova that the complete rectangle can be colored and a 0 white area left off as minimum
-
I looked at the website suggested by rainman. I think it could be a cipher of some sort and you probably have to get the cipher key from some previous rounds??
-
This is the same case as that of a point in the triangle: A line has zero area, so any line on its own can not bound any area.
Lets assume that a group of lines form an infinitesimally small area within the rectangle. Then for any point within this area, there is a line that passes through this point at each and every angle from 0 to 360 degrees. For this to be possible, there are 2 lines that are also perpendicular to the sides of the rectangle. However, this is not possible; if you have 1 line perpendicular to the side, it will keep tracking the same line and never change direction, so the other perpendicular line can not be made. Therefore, there is not even an infinitesimally small area covered by the lines within the rectangle.
The minimum area of the white rectangle then is the area of the rectangle itself. -
Now what if the friend walks in the bar and he sees the first person drinking but the next person isn't drinking, does this contradict the axiom?
No, it doesn't contradict the axiom. In truth, the actual probability that a person is drinking or not is 0<= p <= 1. However, as there is no physics that determines what the exact probability of everyone or any one person drinking would be, one must rely on inference and induction.
-
working backwards by induction, the test must be today!
If you can prove by induction that the test is today, how can it's date be a surprise?
Because the announcement that there will be a surprise test can be made on any random day, which is a surprise.
-
If I took this reasoning to the doctor instead, then either he is inconsistent or conceited as he would have the same "diagnosis" of believing and making mistakes...
I would therefore advise the man to leave the psychiatrist's clinic. The man is alright, he's just human! -
While in school our math teacher gave us a funny and a practical example of mathematical induction. At the start of the class, she said "before the end of this month, you will have a surprise quiz. Can anyone guess when it will be?" We all gave some random days and she ultimately handed us the quiz in the next 10 mins!
Thinking back, here's how I reason it...
Let's say the month is of 31 days. If by the 30th, there is no test done, it will be done on the 31st and is no longer a "surprise test". The test must therefore be done before the 31st.. Now, on 30th, if there has been no test by the 29th, the test must be done before otherwise it will not be a surprise... working backwards by induction, the test must be today! -
He confirmed that everyone was drinking... The first friend's theory is also supported by "induction"
-
-
-
The basic premise of the balance is that:
a) the "system" of dominoes should have its Centre Of Gravity (COG) on the table
b) Any domino on any extremity must have its COG either on the table or on another domino
For 2 dominoes, the 3/4th overhang is possible as follows:
(1 Domino length is 4 units here)
The system of 2 dominoes has its COG at the edge of the table.
For 5 Dominoes, a simple construction could be as follows:
The overhang here is 1 domino.
With this set-up, the COG is at (22x/5x) = 4.4 while the edge is at 5; The whole system can be moved by 0.15 domino length (0.6/4) and still have it stable. The total overhang then is 1.15 domino length.
In fact, a better configuration can be achieved by placing the dominoes as follows:
4 5
3 2
1
The first domino overhangs 0.29 domino length.
The total overhang in this case would be 1.29 domino length.
-
Aha, now I know why couldn't figure it out!
I was reducing the problem to 2 mathematicians, 2 rooms and say 5 or 10 boxes; where as if I understand correctly the explanation from Bonanova, I should have considered all the mathematicians in the world, matching number of rooms, and a much larger number of boxes





Mensa Math/Logic Problems...How to Solve?
in New Logic/Math Puzzles
Posted