
DeGe
-
Posts
133 -
Joined
-
Last visited
-
Days Won
8
Content Type
Profiles
Forums
Events
Gallery
Blogs
Posts posted by DeGe
-
-
-
If I posted this problem, I would ask to clarify:
1) why the lines H and I cannot be parallel;
2) crossing trajectories do not necessarily imply that the ships collide.
BTW, the sea should be endless (so that H does not reach her destination before colliding).
1) Agree. Of course H and I can be parallel. Alternatively, they could even meet/collide at the same point (or just after) the collision between H and F. However, The question is not to find out the exact points at which they collide (if they do).
2) Agree again - that will depend on the relative speeds of the ships. Since no such info is given in the op, the solution must provide for any possible combination of speeds and directions.
The proposed solutions does take that into account.
-
Guys these are three empty bowls A bowL is 500mil , B bowl is 1 Litre, C bowl is 500mil and there is one jar of 1litre water aprat from this 3 bowls so we have to pore water in such a manner in all 3 bowl should have same level of water also once so how will you solve?
Fill up one of the 500 ml jars to a random level (with <333 ml water)
Now fill up the other 500 ml jar so that water level in both jars is same. (I am assuming that the 2 500ml jars are of the same dimensions)
Now empty one of the 500ml jars in the 1000 ml jar. Refill the emptied 500ml jar so that it has again the same level of water as the other 500ml jar.
Now all 3 jars have equal measure of water.
-
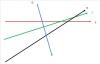
The ships are traveling as below:
Now, for H to avoid the collision with I, he needs to stop for a while before restarting the journey.
The time of rest will depend on the time between the 2 collisions and the times at which the other ships started.
Alternatively, he can change course and follow (for a while) the course that F was coming from and then go in the direction of his destination.
I is E above.
-
Do the straight forward entries and then notice that in column 2, 35+ can be made only by using 56789. This means that for 864x the only possibility is 8934. This means that 9+ in last row can be made using 135 only.
Then in column 6, there remain only 2 possibilities for 15+ and after some more entries, only 1 possible combination remains if you solve column 7 simultaneously. This opens up the grid and everything "flows" thereafter -
Winning strategy is to keep the card out of the first 3 as soon as you see a 9 or higher card.
Reasoning:
The probability that you have all 4 cards below 9 is 32*31*30*29/(52*51*50*49) = 0,133
In this case you lose from $-2 to $-9 with equal probability = 0,133/8 = 0,0166
Now the probability that one of the 4 cards is 9 or higher is 1 - 0,133 = 0,867
Since you stop at the first sight of a 9 or higher card, you stand to win -1,0,1,2,3 with equal probability = 0,867/5 = 0,173
This gives an overall expected winning amount of 0,14 per game you play.
PS: If you decide to stop at 10 higher card only, the expected amount of winning is 0,09 per game. Could be a winning strategy but not the most effective one!For any other choice of stopping, the expecting winning is negative
-
Haha... While doing engineering, we used to ask the first year new comers to do a similar thing (using 11 thousand, 11hundred and 11).
-
I think DeGe's strategy is sound.
The term "toggle" may be adding confusion.
Prisoner 1 always turns the light OFF [or leaves it off]
Every other prisoner is allowed to turn the light ON only once [after they turn it on once, the leave it unchanged]. Other prisoners are not allowed to ever turn the light off.
after day 1 prisoner 1 counts the times he turns it off and after 99 he can safely assume that all have been in the room
Thanx for making it clear.
-
The ships are traveling as below:
Now, for H to avoid the collision with I, he needs to stop for a while before restarting the journey.
The time of rest will depend on the time between the 2 collisions and the times at which the other ships started.
Alternatively, he can change course and follow (for a while) the course that F was coming from and then go in the direction of his destination.
-
I think you need to clarify your question.
As I see it now, it seems very simple and straight forward, to pour 500 ml from one of the small bowls into the 1L bowl. NOw it contains 500ml water. Fill up the other small bowls and you have all bowls with smae measure of water - 500ml.
-
Don't worry about the combinations for 84x or 840x. Just note that the positions of 7 are pretty much fixed for rows 2/3/4.
After doing some preliminary entries that are straight forward, eliminate 2+8 as choice for 10+ in row 1; Then eliminate choices for 6789 simultaneously in columns 5 and 6; You will notice that only one possible combination of 6789 in last 2 rows of column 6 gives you possible solution; with any other combination there are conflicts elsewhere.
Then the grid opens up and you have an easy solution. -
The prisoners decide that who ever is called on the first day will be the one to take the call whether all have flipped or not.
Also they decide that any prisoner (except first) going to the room will toggle the switch on IF it is off otherwise will not toggle the switch. And, any prisoner (except first) will toggle the switch ONLY once.
The first prisoner will always toggle the switch off and count the number of times he does so. When he has a count of 99 toggles to off (other than his own on the first day if the bulb wasn't off) , he announces the passage of all 100 prisoners.-
 1
1
-
-
abs (x) = max(x,-x)
-
The expected value will be 500000/999999 + Sum(2*i/999999)
which is 500000/999999 + 499999*500000/999999
which is (5000002)/999999
which is 250000.250000250000250000...
I stand corrected
-
Let there be 2n coins in the urn at any stage.
Then the bag with smaller number of coins can have 1,2,3,....n coins.
It so happens that the probability for the smaller bag to have 1,2,3... n-1 coins is equal (lets say x) and for it to have n coins is x/2 such that the sum of x*(n-1) + x/2 = 1I got this hypothesis by using brute force - calculating probabilities with total 8,10,12,14,16 coins.
Therefore for 1M coins, the probability for the smaller bag to have 1,2,3,... 499 999 coins is equal and probability for it to have 500 000 coins is half of this probability.
So, 499 999x + x/2 = 1x = 1/499 999.5 = 2/999 999
It follows then that the expected number of coins is 499 999/2 + 500 000/999 999; this is equal to 250 000.000015
So you can pay 250 K for the bag in advance -
In the various settings, there are 6 settings where there are no matches, 3 settings with 1 match, 2 settings with 3 matches and 1 setting with 2 matches.
Given the Judge's claim, there must be 2 matches and the order of boxes is 7, 10.... 2 and the coins respectively are 0,1,2...12
So the prisoner selected box 7 with 0 coins. -
48,50,53
The series is either prime numbers or odd number-1 if the odd number is non-prime11110011
Powers of 3 expressed in binary -
The bartender uses a simple logic: If the numbers of upsides/downsides are odd, then invert 1 glass otherwise invert 2 glasses
So if the configuration is 1-3 or 3-1 up-down, he inverts one glass
If the configuration is 2-2 he inverts 2 glasses
The glasses he selects to invert is either G1 (for odd configuration) or G1 and G2 (for even configuration) after each rotation
G1
G4 G2
G3
By doing so, in 1-3 configuration, he will either make the config 4-0 or 2-2 after the first rotation with a probability of 25% and 75% respectively.
Then each time, he inverts the glasses when they are in an even configuration, the new configuration would be 4-0; or remain 2-2 (with the new configuration as u-u-d-d or u-d-u-d). He has 1/2 probability of making it a 4-0 configuration if the previous configuration was uudd and 0 probability if it was udud.
Effectively, after every alternate inversion of even glasses, he will have 50% probability of making it 4-0.
-
Truth??
-
Nice puzzle
348 x 28
Here's why:
Lets rewrite the puzzle as:
o1 e1 e2
e4 e3
e8 o2 e6 e5
e9 o3 e7
o5 o4 e10 e5
o1 must be less than 5 because e4 multiplied by oee is 3 digit number
o1 is either 1 or 3
If o1 is 1, then the multiplication of oee with e3 with end in 1xxx
So, o1 must be 3
Then e4 must be 2 in order to keep oee x e4 a 3 digit number
e9 is 6 then e8 must be 2 and o5 must be 9
if e8 is2, then e3 is either 6 or 8
If e3 is 6, the carry over needed from e1xe3 is either 3 or 5
in order to get e8o2 as 21 or 23
Then e1 must be 6 or 8
However, e1 must be either 2 or 4 otherwise e9 will not be even
So e3 can not be 6
e3 must be 8
If e3 is 8, e1 can be 2 or 4
Also e2 must be either 6 or 8
because if e2 is 2 or 4, it gives an odd carry over and e6 will then not be even
Now, if e1 is 2, carryover sent to multiplication of 3x8 will be 2 (16 + either 4 or 6 carried over from 6x8 or 8x8) and o2 will not be odd
so e1 must be 4
Finally, for e2 which is either 6 or 8
If it is 6, the individual multiplications of oee with e4 and e3 are ok;
However, if you add them up, it results in OEEE instead of OOEE
With e2 as 8, all the results are ok
-
If the cube was laying flat you would be right. But hanging it by a vertex causes a different shape.
Aha, I answered for hanging by an edge and not vertex.
-
a rectangle
-
The songs sang is Nc2 - N
So, N is 7 (total 14 songs are sung so N must be multiple of 7) -
Are you sure the conversion for the 6 digit number is correct?
For the reasoning that I find compatible for all the numbers (except this one), it should be 100011
The last digit is 1 if it is even or if there is an even occurrence of an odd number; otherwise 0.
The next digits to the left are 0 if the digit to the immediate right is smaller and 1 if it is larger. This logic gets inverted if the last digit is odd and occurs even number of times (the 6 digit number case)



LOTR Telephone
in New Logic/Math Puzzles
Posted