bushindo

Nice problem

I'm not sure how to improve the cycle length. I'd like to see the solution. Nice problem, by the way.

You're right, it's way too small

I'd like to submit a point of view on this problem. I'd like to review the problem first. The crux of the debate, according to my skimming of the last 10 pages, boils down to this. Let A(n), similar to superprismatic's definition, be the chance of initially having n white balls in the bag of 4. We need to have the vector of probabilities [ P( A(2) ), P( A(3) ), P( A(4) ) ] to solve this problem. We are not given information about these states, and this is where mmiguel1 and superprismatic diverges. mmiguel1 argues that in the lack of information about the balls-bag generation process, he will assume that the bag was generated by a binomial process with 4 trials and chance of black ball = .5. superprismatic and the OP, and the CBSE board as well, argue that the uniform distribution is most representative of the lack of information, otherwise known as an un-informative prior in Bayesian statistics, and thus use the vector of probabilities [ P( A(2) ), P( A(3) ), P( A(4) ) ] = [ 1/3, 1/3, 1/3 ]. The uniform distribution is the oldest and simplest un-informative prior, so I can understand where this is coming from. The issue is that the uniform distribution is not the only un-informative prior there is (see http://en.wikipedia.org/wiki/Prior_probability#Uninformative_priors). There are a wide number of un-informative priors, and they probably would yield different answers. One example, for instance, would be to assume that each ball in the bag has a chance of being black p, where p belongs to the Beta distribution with the improper prior Beta(0,0). superprismatic made the point that prior distribution, especially in case with no information, is subjective, which I think is where the discussion should have ended. However, my beef with the problem is that the CBSE puts this problem on a board exam, and presumably expects only 1 right answer, which is derived from assuming a uniform prior distribution as the non-informative prior. If the CBSE taught all their students to always assume the uniform as a non-informative prior, then this is a fair problem as a board exam. It is not, however, valid to post this problem to the brainden and board and expect .6 as the answer, just because the CBSE said so.

That is excellent result. 259% gain on your bankroll in roulette is great. Let's go to Vegas together this weekend.

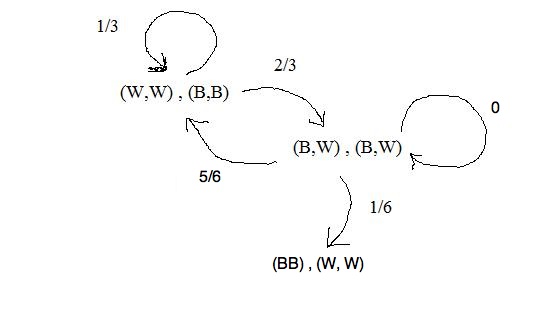
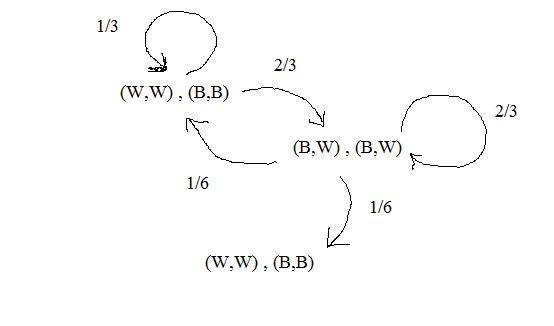
Congrats to mmiguel1 and bonanova, who got the answer. I have a question about bonanova's method. While the answer is correct in this case, would the approach change at all if I change my state movement mechanism From this: "an iteration as the act of randomly selecting a ball from bag A and transferring it to bag B, and then randomly selecting a ball from the four available balls in bag B, and transferring it back to bag A" To this: "an iteration as the act of randomly selecting a ball from bag A and another ball from bag B, and then switching the two balls" Intuition says that the final probability of 3 black balls in bag A will change with the change in state movement mechanism, but it is not apparent from the quick and dirty method.

It seems to be a coincidence.

This is a variation on superprismatic's excellent puzzle White balls/ Black balls. Suppose that we have two bags: bag A and bag B. Bag A contains 3 white balls, while bag B contains 3 black balls. We define an iteration as the act of randomly selecting a ball from bag A and transferring it to bag B, and then randomly selecting a ball from the four available balls in bag B, and transferring it back to bag A. Thus, at the end of each iteration, there are 3 balls in each bag. Suppose we start with 3 white balls in bag A, and 3 black balls in bag B, and apply the iteration above 10 times. Now, if we open up bag A, what is the probability that we will see 3 black balls?

Nice catch. I didn't see that mistake. Your approach is one that i didn't think of. I solved this problem because I learned about Markov random chains before, so the framework is there. I find your solution to be more impressive since it is a brilliant and original application of probability rules and algebra. Well done.

Hi mmiguel1, it really has been a while. Looks like you have been a very productive member on this board. I remember a couple of month ago you had your 1st post, and now you have almost the same post count as me.

Haven't been here for so long. I miss superprismatic's problems.

Some comment

That's a nice proof. I didn't think of that. Here's a clumsier proof using induction

I saw this in a test long ago. In Determinant Tic-Tac-Toe, Player 1 enters a 1 in an empty 3×3 matrix. Player 0 counters with a 0 in a vacant position, and play continues in turn until the 3×3 matrix is completed with five 1’s and four 0’s. Player 0 wins if the determinant is 0 and player 1 wins otherwise. Assuming both players pursue optimal strategies, who will win and how?

That's some childhood you got, maybe it's a polish thing. I got mostly spanks on my mother's knee. I'll supplement the hint that magician gave earlier

I saw this problem in a test long ago. Assume that we have a sequence of 17 distinct integers. Show that there exist at least 1 subsequence of 5 integers that form an increasing or decreasing sequence. For instance, let the sequence of 17 distinct integers be 9, 13, 6, 1, 11, 7, 16, 3, 15, 10, 2, 5, 12, 4, 14, 8, 17 Then there is a increasing subsequence of length 5 in (1,3,5,8,17). There is also a decreasing subsequence of (16,15,10,5,4). Show that the statement in the second paragraph is true for all sequences of 17 distinct integers.

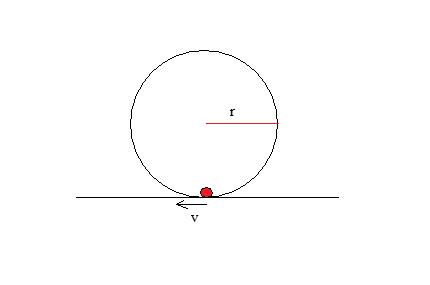
Let's say there's a circular track placed perpendicular to the ground as in the following image The track has radius r. At the bottom of the track, there is a ball with horizontal velocity v. What is the minimum velocity v such that the ball will travel along the track to make a full circle without falling off the track at any point. Assume that there is no friction, and that the radius of the ball is very small relative to the radius of the track.

The 2500th digit from right to left is actually an even number.

Those who are intrigued by this problem may be interested in this theorem

Nice solution. It's good to see another Latex user on this board.

General N-hats solution

Sorry for not updating earlier as promised. I was away at camp for three days without access to internet.

It is possible to construct a guaranteed non-losing strategy, regardless of what the other guy does.

Here's a way to derive the answer using matrices. This probably isn't the solution you had in mind. I'd like to know that solution, though.