bonanova

Yes.

Now, what was it we were talking about? Oh yes ... wherrzzz Beeel? I'll tell you. You know why I tell you? Because Bill would want me to. But this time the old man was not talking to the impossibly gorgeous Beatrix Michelle Kiddo. It was to a guy. A guy who was on a mission to kill Bill. A guy with the name of Al, Jack, Joe or Tom. Which one? Well, it's your job to determine which. Here's what we know from police interviews that followed the discovery of Bill's cold body on a lonely stretch of country road late last night, along with the fatal gun that belonged to one of them ... the murderer. So read on and see where the evidence leads. But fair warning, exactly half of each of the suspects' four statements are lies. Al: I didn't do it. Tom did it. Sure I own a gun. Joe and I were playing poker last night when Bill was shot. Jack: I didn't do it. Al did it. Joe and I were at the movies last night when Bill was shot. Bill was shot with Joe's gun. Joe: I was asleep when Bill was shot. Al lied when he said that Tom killed Bill. Jack is the only one of us who owns a gun. Tom and Bill were pals. Tom: I've never fired a gun in my life. I don't know who did it. Joe doesn't own a gun. I never saw Bill until they showed me the body. Who was the rat who done poor Bill in?

Plato: Good morning, class, today's lesson is on probability. Aristotle: Fantastic. I'm headed to Vegas this weekend, and I can use some pointers. P: Curb your enthusiasm kid, this is serious stuff. Here, roll this pair of dice, but don't look at the the result. OK, good. Now without looking, tell me the probability that you rolled a seven. If you're going to play craps this is important. By the way, I can tell you that one of your dice is a four. A: Hmm... So I could have rolled 41 42 43 44 45 46 14 24 34 54 or 64, all with equal likelihood, with 34 and 43 making seven. That's a probability of 2/11. P: You're on a roll kid, now let's do it again. Great. Again without looking, what's the probability you rolled a seven? By the way, I can tell you one of your dice is a one. A: So I could have rolled 11 12 13 14 15 16 61 51 41 31 or 21, with 16 and 61 making seven. Hmm... it's the same as before - 2/11. P: And if I had told you one of your dice was a five? A: Well ... I guess it really doesn't matter what number you tell me. It will always come out the same. The probability will be 2/11. P: So what can we deduce from that? A: That the probability of two dice making seven is ... 2/11. But wait... Hey, you're not really Professor Plato, are you? P: No. I'm an insurance salesman. So ... what exactly is the probability of making seven?

Yes. The restriction is only that they can't read each others' labels.

Four identical boxes, each box containing 3 balls, each ball being either black or white, were placed before four men: Al, Bert, Cal and Don. No two boxes contained the same selection of ball colors. Each box bore a label that correctly identified the contents of one and only one of the boxes, but no individual box bore its correct label. After each man, at random, was given one of the boxes, they were given the following test. Each in turn, and out of sight of the others, was to blindly remove two of the balls from his box, read the label on his box, and then endeavor to tell to the others the color of the third ball, which remained in the box. It did not seem a difficult task, but the results were a bit surprising: Al: I've drawn two black balls. I can tell you the color of the third ball. Bert: I've drawn one white ball and one black ball. I can tell you the color of the third ball. Cal: I've drawn two white balls. I'm not able to tell you the color of the third ball. Don: (who was blind, and could not read his box's label) I don't need to draw. I can tell you the colors of the balls in my box. I can tell you the color of the third ball in each of the others' boxes. And then he proceeded to do so. How did he tell?

You're right. Nice solve.

You can eliminate the second case else there would be another X in the puzzle statement. Nicely done.

Didn’t all break ... just rules out the case that all broke ... anything else is possible Between Ed and Jim means beat one and lost to the other. I have somewhat different answer.

Ok what I was looking for is that if no one called their initial then they must have alternated teams when they formed the circle. So that fact didn’t need to be given as a separate condition or assumed. Initials occurring in odd positions of the alphabet must have held even positions in the circle.

Sharpen your pencil for this one. Each period is a missing digit. . . . X . ======= X . . Y . X Y ------- . Y X Y What two numbers are being multiplied?

When four friends, Bill, Ed, Jim and Tom, began their foursome at Fairview Links last Saturday, they discovered to their dismay that no one had brought a pencil to keep their scores. And well let's just say that in the clubhouse afterward there was some confusion. Here are four "facts" that each player remembered. But fair warning, it turns out only two of each group of statements are true. And, if it helps, they all correctly remembered that no two players had the same final score. Bill: I beat Jim and Tom. Ed shot 111. Jim took 6 on the last hole. None of us broke 100. Ed: Bill wasn't last. I was the winner. Jim finally broke 100. I shot 98. Jim: I beat Bill and Ed. The last hole was not my best. We didn't all break 100. Tom wasn't the winner. Tom: Ed beat Bill. I was the winner. Bill placed between Ed and Jim. The last hole was Jim's best. That's it. But surely by now you know what order they actually placed.

In a dream I visited a city named Ten Islands, a charming archipelago connected by a system of bridges, five of which led to the mainland. Four of the islands were serviced by four bridges, three others by three bridges and two others by two bridges. The final island could be reached by only one bridge. The city was well laid out, and the view from each of the bridges provided a new and enchanting visual experience. I shared the dream later with my son, remarking again and again of the city's beauty. Even if you hadn't mentioned the fact to me, Dad, I would have told you this was not a real experience, he replied. Ten Islands, as you described it, could not exist in this world, only in a dream. How could he be certain of that?

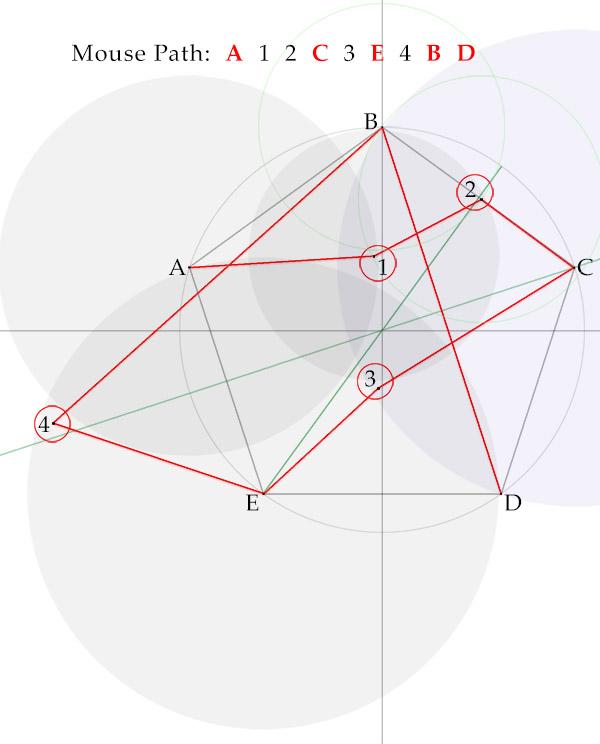
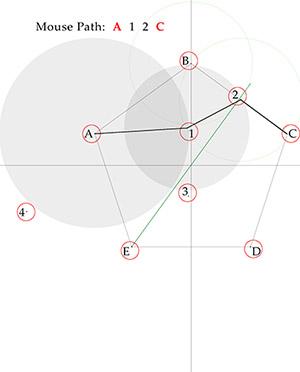
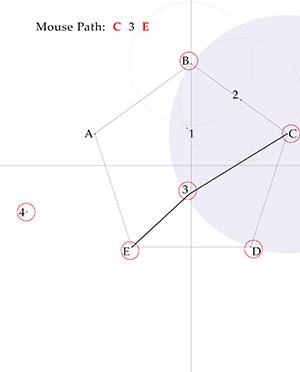
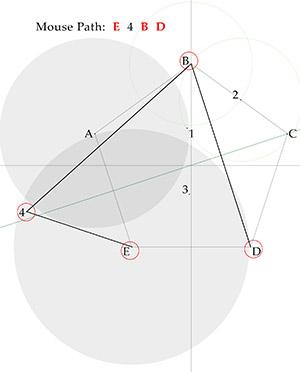
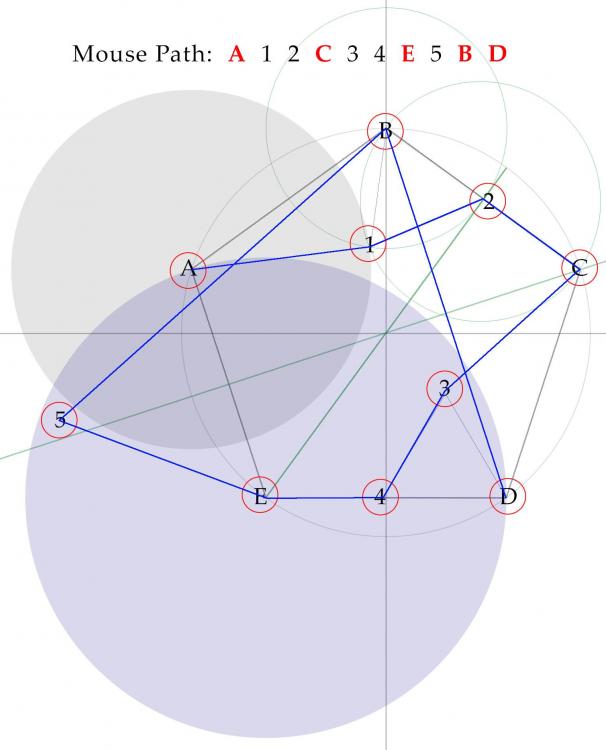
With discussion help from @plasmid, here is a 9-crumb solution. Kudos again for an engaging puzzle. Path A 1 2 C Path C 3 E Path E 4 B D

I asked the players about that last night. Jenkins, Babcock and Morris recalled they were not standing next to a team mate; then several others said the same. Smith and Peters agreed, but added that they were quite certain they weren't told to alternate, noting the process was supposed to make home team selection a random process. They all agreed that it might have happened by chance.

What precludes the mouse from going from G(2) to G(5)? (My eyes are getting bleary ...)

I think there's a proof for the pentagon case.

This was a fun puzzle.

Kudos to the pretty girl in the green dress.

@plasmid was discussing finances with his planner the other day. After they reviewed tax returns and year's worth of receipts, the advice he received was just this: S P E N D - L E S S ========= M O N E Y You's think so, he replied, but I've determined that this is quite impossible. Is he right?

I understand that the mouse goes to the nearest crumb, and that "nearest" means shortest euclidean (straight line) distance. So (haven't read the spoiler yet) I never conceived the mouse would get advantage by doing otherwise. I'm assuming the mouse is playing strictly according to his own hunger advantage. Am I right about that? Oh wait. you're saying that Give me a day or two to work on that?

@CaptainEd @plasmid

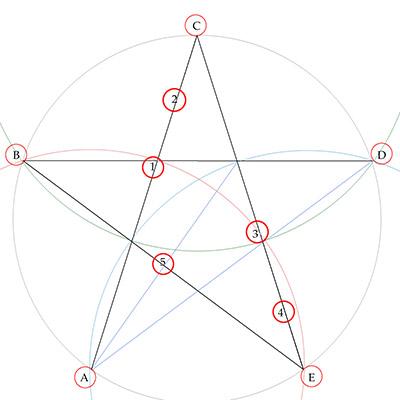
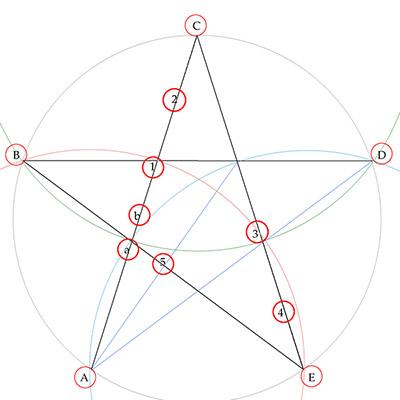
@plasmid Interesting puzzle and thanks for the call out. EDIT: Thought this was optimal, but now have read @CaptainEd's solution. Tip of the cap, Nice going. FWIW, my best efforts follow .... Breadcrumbs (red circles) are placed at the five vertices A B C D and E. Object is for our mouse to take four straight paths: AC, CE, EB, and BD. Because we have a greedy mouse that goes to the nearest snack, it will move from a vertex to an adjacent vertex whenever it has an uneaten crumb. That must be prevented. So we draw inter-vertex-radius circles -- a red circle centered on A, a green circle centered on C and a blue circle centered on E -- to help define advantageous areas to place our minimum (M) count of additional tasty crumbs to keep our mouse on its intended path. It is quickly evident that M can't be less than 5. (First-pass solution.) Second-pass solution.

At lunch yesterday four students, Al, Bill, Jack and Tom (last names Conner, Morgan, Smith and Wells, in some order) amused themselves by dealing poker hands to all, with the winner being the holder of the best hand. The winner of the first hand was to collect 10 cents from the other three; the second-game winner would collect 20 cents each; the third winner get 30 cents each; and so on. When the bell rang for afternoon classes to begin, four hands had been dealt, with each student winning once, in this order: Jack, Morgan, Bill and Smith. At the outset Tom had the most money, but at the end Wells had the most. What are the students' full names?