bonanova

On the right track. We need at least three trees per row.

This has languished for a couple of weeks ...

So the answer is 12 trees making 18 rows. Can you draw the layout?

Use each of these numbers once, 1 5 6 7 along with + - x / ( and ), to make 21

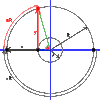
Consider my diagram for straight line tangential escape. From the red dot [landing point] move clockwise a small angle DELTA a and draw a blue dot. Call the shore length between the dots h. Draw an arc centered on the rower's starting point clockwise from the red dot [radius is y, the rower's distance to the red dot.] Call this arc s. Now draw a line from the blue dot back to the rower's starting position. The distance from the blue dot on the shore to the intersection with arc s is the change DELTA y of the rower's distance to the blue dot instead of the red dot. The red dot, blue dot and intersection point form a right triangle whose hypotenuse is h = R.DELTA a and short side is DELTA y and included angle is a. Thus cos(a) = DELTA y / R DELTA a Letting DELTA a go to zero, with have the rate of increase path for the rower: dy/da = R cos(a) Call the ogre's path O. His path increases by h, the shore length between the red and blue dots: DELTA O = R DELTA a. Again, in the limit we have dO/da = R So with respect to the angle a, the rower's and ogre's paths increase in a ratio of cos(a). Recall that cos(a) = 1/f = the speed ratio of ogre and rower. Thus, the difference in arrival time for the two racers with respect to angle is zero at the red dot. This means the rower's advantage over the ogre is either a maximum or a minimum at a. Note that the triangle we drew actually has curved sides, so the equality is only strict as DELTA a goes to zero. They curve away from each other, so that DELTA y increases super linearly, while DELTA O increases linearly with DELTA a. Thus, for angles greater than a, the ogre gains an advantage. The rower's advantage is thus a maximum. Conclusion: the red dot is the optimal landing point, and a straight line is the shortest distance to it. Q.E.D.

I agree with that logic. I've now also verified with differential analysis that for angles greater than a the rower's path increases more than the ogre's path. Details in next post.

It seems, you have proven that the tangential straight line escape is the optimal path. I'll try to put put a simpler perspective on this whole Ogre-Maiden business using BMAD's Dog Freedom recent problem in this forum. It appears, there is no spiral escape. But don't tell the maiden. I'm still surprised... Differential analysis at the tangential landing point should be able to confirm or deny it. That is, if the landing point is moved a very small amount clockwise. There might then be a tractable expression for differential change in speed ratio. First-order perturbation theory it's called. Like using only the first term in a Taylor series expansion of the various quantities. The same idea as L'Hopital's rule. As a last gasp I might look at it, but I feel a bit burned out.

Not all them. I'm not making any progress. Any tips for analyzing this?

I would argue that this question is a tricky question not a trick question. Too find the Range of yard for the dog you must consider ALL possibilities but you guys have only considered the house to be rectangular. Yes I did make that assumption. Since it's late at night and my eyes are drooping, I'm sticking with the assumption.

Your task is to debunk the rumor that I am psychic. Should not be hard. . You're right. The integers must be positive. Good catch.

Sure. There are an infinite number of tie points. Do you want a general equation? Do you want the tie point for max or min? Something other?

For a straight line escape, it seems clear that the optimal angle is between the zero (straight line to the nearest point on the shore) and the tangential line escape. Past the tangential escape, maiden re-enters her inner circle going towards the Ogre causing him to change the direction. You have calculated the precise rate O:M rate (f) for the tangential escape. And it is better than the nearest point escape. However, for the other angles in between those two, calculation of maiden's trip is a bit more messy. I think this problem still has a suspense left and warrants further investigation. If re entering the small circle is the criterion that gives advantage to ogre to change his direction then I think we know the optimal straight-line escape path. Reason: I postulate the advantage increases initially with angle from radial, and then does one of two things: It increases monotonically with angle from radial to tangential. If so, we're done. A very quick and dirty analysis shows the advantage is still increasing with angle at tangential. It reaches a maximum at some angle between radial and tangential. If this is true, the advantage would be decreasing with angle at tangential. But analysis says it's increasing. It seems clear from the diagram that every degree of angle added to the escape path adds proportionately to the ogre's path. While the rower's path increases to a much lesser degree. In particular, the 45 degree case was analyzed rigorously and shows an advantage intermediate to those of radial and tangential. Only when the ogre can advantageously change direction would further increase in angle be ill advised. It would be interesting to show that going beyond tangential incents ogre to reverse direction. Rower would then reverse as well, putting us in zig zag mode.

Conjecture: By saying "whatever shape the pentagon has" you are not limiting the discussion to regular pentagons. True?

It is a lot simpler than that for the zen master Ogre. The Ogre ignores where the maiden looks, where she goes, and where she intends to go. Ogre simply draws an imaginary straight line from the center of the lake, through the boat, to the shore; and heads for that spot using the shorter arch. Insofar as the optimum is concerned, it is the Ogre who determines the path -- not the maiden. The maiden reacts to Ogre's moves, not other way around. If the maiden wanders back into her inner circle r, that could make the Ogre change the direction when the boat crosses straight line drawn from the Ogre to the center of the lake. Then the young lady would be going towards Ogre rather than away from him. (Not an optimal strategy.) Presently, we are solving the sub-problem, where the maiden after leaving her inner circle goes in a straight line towards some point on the shore. We must find, that point. Bonanova suggested going off the inner circle on a tangent line. That gives a better ratio than going in a straight line to the nearest point on the shore. However, I don't believe it is the optimum. The numbers I have given in the post #23 inside the spoiler are off. But then, as everyone knows, I am siding with Ogre. Blame it on the cold, Prime. I am not convinced that tangential is optimal - it may not be enough! It's easy to overlook that r is one of the unknowns. I did overlook that r is one of the unknowns because of cold and my partiality to Ogre's cause. Still I don't see that the problem is solved even for a straight line escape. By the way, I did not see the answer by Phaze to which you referred. Is BD not displaying some of the posts to me? Good catch Prime, and I have no health excuse. Apologies. I've edited my post 25 to properly attribute you as the solver. Edit: We can't continue indefinitely increasing the angle however. At some point it will become to the ogre's advantage to reverse his direction.

It is a lot simpler than that for the zen master Ogre. The Ogre ignores where the maiden looks, where she goes, and where she intends to go. Ogre simply draws an imaginary straight line from the center of the lake, through the boat, to the shore; and heads for that spot using the shorter arch. Insofar as the optimum is concerned, it is the Ogre who determines the path -- not the maiden. The maiden reacts to Ogre's moves, not other way around. If the maiden wanders back into her inner circle r, that could make the Ogre change the direction when the boat crosses straight line drawn from the Ogre to the center of the lake. Then the young lady would be going towards Ogre rather than away from him. (Not an optimal strategy.) Presently, we are solving the sub-problem, where the maiden after leaving her inner circle goes in a straight line towards some point on the shore. We must find, that point. Bonanova suggested going off the inner circle on a tangent line. That gives a better ratio than going in a straight line to the nearest point on the shore. However, I don't believe it is the optimum. The numbers I have given in the post #23 inside the spoiler are off. But then, as everyone knows, I am siding with Ogre. Blame it on the cold, Prime. I am not convinced that tangential is optimal - it may not be enough! It's easy to overlook that r is one of the unknowns.

The difference coming from [my] using finite 1-minute steps. You allowed time to prefix "Unaccustomed as I am to public speaking ..." Nice puzzle.

Prime has got the answer, at least as far as I have analyzed it. That being true, I will post my analysis and people can take pot shots at improving it.

Yes. Nice solve. It was common to re-use a name after an infant's death. There were sibling Salvador Dalis. The older one died young, the younger one became famous.

Yes. Verified by starting at the first turn and noting 80/40 = 40/[100-80]